第 33 章重要概念回顾

33.1 概率论统计推断要点

下面我们一起用二项分布的概念 ($n$ 个对象中 $K$ 个“事件”)，来复习概率论学派的统计推断要点。

模型，the Model。一个统计模型，描述的不仅仅是我们研究的人群的一些特征，而且通常一个模型还可提供如何从人群中收集该样本的信息。
用二项分布的概念来解释，人群是众多个体的集合，他们中的一部分占比 $\pi$ 的人身上发生了某个事件。从这个人群的集合中，我们随机抽取 $n$ 个对象作为研究样本，该样本中有 $K$ 个人身上发生了事件。此时，我们说 $K$ 服从人群比例为 $\pi$ 的二项分布：$K \sim \text{Bin}(n,\pi)$。
参数，parameters。模型中的参数反映了人群的某些特征。在实际应用中，从来没有“人类”能知道人群参数的真实值，渺小的我们从人群中抽取样本，用于推断 “上帝才知道的” 这些代表了人群特征的参数。
在二项分布的情境下，有且只有一个人群参数，人群中事件的比例 $\pi$。
参数估计量，parameter estimators。估计量是样本的统计量，被用来估计未知的总体参数。估计量 estimator，是一个随机变量，是我们计算估计值的一般形式。估计值 estimate，是每个样本通过统计模型计算获得的估计量的真实值，每采样一次，计算获得的估计值理论上会略有不同。
二项分布的上下文中，人群事件比例– 这一参数$\pi$ 的天然估计量是$\hat\pi = \frac{K}{n}$，当一个样本中发现$ K = k$，该样本给出的估计值是$$。
研究假设，hypotheses。研究假设是实验前我们提出的要被检验的一些关于人群某些特征参数的 “陈述 statement”。可以是猜想参数等于某个特定值，或者多个参数大小相同。
二项分布的数据里，只有一个人群参数，$\pi$。可能提出的零假设和替代假设有很多，$\pi = 0.5 \text{ v.s. } \pi \neq 0.5$ 是其中之一的复合型假设。

33.2 似然

如果一个模型只有一个参数 $\theta$，样本数据已知的话，该参数的似然为：

\[\text{L}(\theta | \text{data}) = \text{Pr}(\text{data}|\theta)\]

其中，$\text{Pr}(\text{data}|\theta)$ 对于离散型变量，是概率方程 probability function；对于连续型变量，则是概率密度方程 probability density function (PDF)。

对数似然，就是上面的似然方程取自然底数的对数方程：

\[\ell(\theta | \text{data}) = \text{ln}\{ \text{L}(\theta | \text{data}) \}\]

33.3 极大似然估计

当数据收集完毕，从获得的数据中计算获得的能够使似然方程/或对数似然方程取得极大值的$\theta$ 的大小，被叫做极大似然估计$\text{(MLE)}$ ，且通常数学标记会在参数上加一顶帽子： $\hat\theta$。收集不同的样本，在相同的似然方程或对数似然方程下，极大似然估计不同。

许多问题，我们获得极大似然估计的方法是先定义好模型的似然方程，然后求该方程的一阶导数之后计算使之等于零的参数值大小就是$\text{MLE } \hat\ theta$。此时，你还要记得再求一次二阶导数，看是否小于零，以确保前一步计算获得的值给出的似然方程是极大值。
更多的时候我们用对数似然方程以简化计算过程：

\[ \begin{aligned} \left.\frac{\text{d}}{\text{d } \theta}\ell (\theta | \text{data})\right\vert_{\theta=\hat{\theta}} &= \ell^\prime(\hat\theta) = 0 \\ \left.\frac{\text{d}^2}{\text{d } \theta^2}\ell (\theta | \text{data})\right\vert_{\theta=\hat{\theta }} &= \ell^{\prime\prime}(\hat\theta) < 0 \end{aligned} \]

我们只关心似然方程的形状，所以方程中不包含参数的部分可全部忽略掉。
$\text{MLE}$ 的一些关键性质：
1. 渐进无偏 asymptotically unbiased：当 $n\rightarrow \infty$ 时，$E(\hat\theta) \rightarrow \theta$；
2. 一致性 consistency：随着样本量的增加，$\hat\theta$ 收敛于 (converges) 总体参数 $\theta$；
3. 渐进正态分布asymptotically normality：随着样本量增加，$\hat\theta$ 的样本分布收敛于(converges) 正态分布，方差为\[E[-\ell^{\prime\prime}( \theta)]^{-1}=[-\ell^{\prime\prime}(\hat\theta)]^{-1}\]
4. 恒定性invariance：如果$\hat\theta$ 是$\text{MLE}$，那么$\theta$ 被数学转换以后$g(\theta)$ 的方程的$\text{MLE}$ 是$ g()$
似然理论可以直接拓展到多个参数的情况。一般地，如果一个模型有$p$ 个参数$\mathbf{\theta} = (\theta_1, \theta_2, \cdots, \theta_p)^T$，这些参数在给定数据的条件下的似然方程为：\[\text{L}(\mathbf{\theta} | \text{data}) = \text{Pr}(\text{data} | \mathbf{\theta})\] 其中，概率(密度) 方程在多个参数时变成联合(joint) 概率(密度) 方程。似然，也是各个参数的联合似然方程。此时，参数向量 $\mathbf{\theta} = (\theta_1, \theta_2, \cdots, \theta_p)^T$ 的方差协方差矩阵的估计量为：

\[ \hat{\text{Var}}(\mathbf{\hat\theta}) = - \left( \begin{array}{c} \frac{\partial^2\ell}{\partial\theta^2_1} & \frac{\partial^2\ell}{\partial\theta_2\partial\theta_1} & \cdots & \frac{\partial^2 \ell}{\partial\theta_k\partial\theta_1} \\ \frac{\partial^2\ell}{\partial\theta_1\partial\theta_2} & \frac{\partial^2\ell}{\partial\theta^2_2} & \cdots & \frac{\partial^2 \ell}{\partial\theta_k\partial\theta_2} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2\ell}{\partial\theta_1\partial\theta_k} & \frac{\partial^2\ell}{\partial\theta_2\partial\theta_k} & \cdots & \frac{\partial ^2\ell}{\partial\theta^2_k} \\ \end{array} \right)^{-1}_{\theta=\hat\theta} \]

Tips: typing vcov(Modelname) command in R will display this estimated variance-covariance matrix for the parameter estimates.

回到二项分布数据的例子：

\[ K \sim \text{Bin}(n, \pi) \]

如果我们样本的观测数据是$K=k$，对数似然方程一次微分等于零以后求得的参数$\pi$ 的$\text{MLE}$ 是$\hat\pi = \frac{k}{ n}$。所以参数 $\pi$ 的估计量是 $\frac{K}{n}$。 $\hat\pi$ 的方差估计量是：

\[ \hat{\text{Var}} (\hat\pi) = \frac{\hat\pi(1-\hat\pi)}{n} \text{ for } \hat\pi = \frac{k} {n} \]

33.4 关于假设检验的复习

极大似然估计可以有三大类检验方法：似然比检验法 likelihood ratio test；Wald 检验 Wald test；Score 检验 Score test。

似然比检验法 likelihood ratio test (LRT) (Section 15.2)：

\[ -2llr(\theta_0) = -2\{ \ell(\theta_0) - \ell(\hat\theta) \} \]

零假设条件下 (Under $\text{H}_0$:)

\[ -2llr(\theta_0) \sim \chi_1^2 \]

这个对数似然比的统计量可以和自由度为 1 的卡方分布作比较，计算反对零假设的证据的强度大小。如果显著性水平是 $\alpha$，那么下面条件成立时，可以认为反对零假设的证据强度大到足以拒绝零假设。

\[ -2llr(\theta_0) > \chi^2_{1, 1-\alpha} \]

Wald 检验 (Section 15.3) 是一种利用二次方程近似法对似然比检验进行近似的手段。其检验统计量是

\[ \begin{aligned} (\frac{M-\theta_0}{S})^2 & \sim \chi^2_1 \\ \text{Where } M & = \hat\theta \\ S^2 & = \frac{1}{-\ell^{\prime\prime}(\hat\theta)} \end{aligned} \]

Score 检验 (Section 15.4) 是另一种利用二次方程近似法对似然比检验进行近似的手段。其检验统计量是

\[ \begin{aligned} \frac{U^2}{V} & \sim \chi^2_1 \\ \text{Where } U & = \ell^\prime(\theta_0) \\ V & = -\ell^{\prime\prime}(\theta_0) \end{aligned} \]

如果对数似然方程本身就是一个二次方程(数据服从完美正态分布状态，且总体方差已知时)，这三大类的检验法其实计算获得完全一样的$p$ 值，提供完全一致的证据。多数情况下，三大类检验法的结果是近似的。关于三种检验法的比较可以参考过去总结的章节 (Section 15.5)

33.4.1 子集似然函数

当统计模型中的部分参数是噪音参数 (nuisance parameters) 时，我们需要用到子集似然函数法(Section ??) 来去除噪音参数的影响,，只检验我们感兴趣的那部分参数。

33.5 线性回归复习

33.5.1 简单线性回归

假设对于 $n$ 名研究对象，我们测量个两个观测值 $(y_i, x_i)$，那么用线性回归模型来表示这两个测量值估计的参数之间的关系就是：

\[ \begin{aligned} y_i & = \alpha + \beta x_i + \varepsilon_i \\ \text{Where } & \varepsilon_i \sim \text{NID}(0,1) \end{aligned} \]

或者用另一个标记法：

\[ Y_i | x_i \sim N(\alpha + \beta x_i, \sigma^2) \]

33.5.2 多元线性回归

如果预测变量有两个或者两个以上 $(x_i, \;\&\; z_i)$，那么描述这两个预测变量和因变量之间的多元线性回归模型可以写作：

\[ y_i = \alpha + \beta x_i + \gamma z_i + \varepsilon_i \]

此时， $\beta$ 的含义是，当保持 $z$ 不变时，$x$ 每增加一个单位，$y$ 的变化量。用这个模型，我们默认$z$ 保持不变的同时无论取值为多少， $x, y$ 之间的关系是不会变化的，我们用这个模型来调整(adjust) $z$ 的混杂效应(confounding effect) (Section 26.5)。

当然我们也可以考虑当$z$ 取值不同时， $x, y$ 之间的关系发生改变，只要在上面的多元线性回归方程中加入一个交互作用项即可(Section 29 )。

\[ y_i = \alpha + \beta x_i + \gamma z_i + \delta x_i z_i + \varepsilon_i \]

增加了交互作用项最大的变化是，$x_i$ 的回归系数$\beta$ 的含义发生了改变：当且仅当$z = 0$ 且保持不变时，$x$ 每增加一个单位，$ y$ 的变化量。如果 $z = k \neq 0$ 且保持不变，那么 $x$ 每增加一个单位，$y$ 的变化量则是 $\beta + k\delta$。

33.5.3 简单线性回归的统计推断

一个给定的样本 $(y_i, x_i), i = 1, \cdots, n$ ，其对数似然方程是

\[ \ell(\alpha, \beta, \sigma^2 | \mathbf{y, x}) = -\frac{1}{2\sigma^2}\sum^n_{i=1}(y_i - \alpha - \beta x_i)^2 \]

分别对 $\alpha, \beta$ 求微分之后可以获得他们各自的 $\text{MLE}$：

\[ \begin{aligned} U(\alpha) & = \ell^\prime(\alpha) = \frac{1}{\sigma^2}\sum_{i=1}^n (y_i - \alpha - \beta x_i) \\ U(\beta) & = \ell^{\prime}(\beta) = \frac{1}{\sigma^2}\sum_{i=1}^n x_i(y_i - \alpha - \beta x_i) \\ U(\hat\alpha) & = 0 \Rightarrow \hat\alpha = \bar{y} - \hat\beta\bar{x} \\ U(\hat\beta) & = 0 \Rightarrow \hat\beta=\frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\ sum_{i=1}^n(x_i-\bar{x})^2} = \frac{\sum x_iy_i - n\bar{x}\bar{y}}{\sum x_i^2 - n\bar {x}^2} \end{aligned} \]

注意到和线性回归章节中推导的过程不同(Section 23.4.1)，当时我们用的是最小二乘法，这里我们用的是光明正大的极大似然法，同时也证明了最小二乘法获得的$\hat\alpha,\hat\beta$ 是他们各自的$\text{MLE}$。

另外，残差方差的 $\text{MLE}$ 也可以用上面的方法推导出来，同样和之前的方法 (Section 23.5) 做个对比吧：

\[ \begin{aligned} U(\sigma^2) & = \ell^\prime(\sigma^2) = -\frac{n}{2\sigma^2} + \frac{1}{2\sigma^4}\sum_{ i=1}^n(y_i - \alpha - \beta x_i)^2 \\ U(\hat\sigma^2) = 0 & \Rightarrow \hat\sigma^2 = \frac{\sum_{i=1}^n(y_i - \hat\alpha - \hat\beta x_i)^2} {n} \end{aligned} \]

这个残差方差的$\text{MLE}$ 其实不是一个无偏估计，它只是一个渐进无偏的估计(需要除以$\frac{n-2}{n}$)，所以，当一个线性回归模型中有$p$ 个参数时：

\[ \hat\sigma^2 = \frac{\sum_{i=1}^n(y_i - \hat\alpha - \hat\beta_1 x_{i1} - \hat\beta_2 x_{i2}\cdots)^2} {n - p} \]

线性回归时残差方差的检验统计量服从 $F$ 分布 (Section 25.2.6)。

33.6 GLM例1

33.6.1 建立似然方程

对下列不同的情形，写下其

统计学模型
指明模型中的参数
推导该参数的对数似然方程

33.6.1.1 在 $n$ 名对象中观察到 $k$ 个事件。

统计学模型: $K$ 是随机变量，指代事件的数量，$K \sim \text{Bin}(n, \pi)$。每个观察个体中发生事件的概率相互独立且相同。
模型参数: $\pi$ 是模型参数，指代事件发生的概率。
对数似然的推导

概率方程 (probability function):

\[ \text{Pr}(K = k) = \binom{n}{k}\pi^k(1-\pi)^{n-k}, k = 0,1,\cdots,n \]

似然方程 (likelihood function):

\[ L(\pi|k) = \binom{n}{k}\pi^k(1-\pi)^{n-k}, 0<\pi<1 \]

对数似然方程 (log-likelihood function):

\[ \ell(\pi|k) = k\log\pi + (n-k)\log(1-\pi) + \text{terms not involving } \pi, 0<\pi<1 \]

33.6.1.2 测量 $n$ 名研究对象的总胆固醇浓度 (mmol/l)，已知人群中总胆固醇的测量值呈正态分布且方差为 $4$ (mmol/l)²。

统计学模型: 用 $Y_i$ 表示每个个体测量获得的总胆固醇浓度值。它们是独立同分布的随机变量 (independent and indentically distributed, i.i.d. random variables): $Y_i \sim N(\mu, 2^2 = 4)$。
模型参数: 总体均值 $\mu$。
对数似然的推导:

概率密度方程 (probability density function):

\[ \begin{aligned} f(y_1, \cdots, y_n) & = f(\mathbf{y}|\mu) = \prod_{i = 1}^n f(y_i | \mu) \\ & = \prod_{i=1}^n \frac{1}{\sqrt{2\pi2^2}}e^{-0.5(\frac{y_i-\mu}{2})^2} \\ & = [\frac{1}{\sqrt{2\pi2^2}}]^ne^{-0.5\sum_{i=1}^n(\frac{y_i-\mu}{2})^2 } \\ & -\infty < y_i < + \infty \end{aligned} \]

对数似然方程 (log-likelihood function):

\[ \ell(\mu|\mathbf{y}) = -\frac{1}{2\times2^2}\sum_{i=1}^n(y_i - \mu)^2 + \text{terms not involving } \mu, -\infty < \mu < + \infty \]

33.6.2 建立对数似然方程

对下列不同的情形，写下其

参数的对数似然方程
推导极大似然估计
计算极大似然估计量
绘制对数似然方程的示意图

33.6.2.1 在 10 名研究对象中观察到 3 个事件

对数似然方程是

\[ \ell(\pi) = k\log\pi + (n-k)\log(1-\pi) \]

极大似然估计的推导

\[ \ell^\prime(\pi) = 0 \Rightarrow \frac{k}{\pi} - \frac{n-k}{1-\pi} = 0 \\ \Rightarrow \hat\pi = \frac{k}{n} \]

极大似然估计量 $\hat\pi = 3/10 = 0.3$
绘制对数似然方程的示意图

pi <- seq(0,1, by = 0.0001)
likelihood <- 3*log(pi) + 7*log(1-pi)
plot(pi, likelihood, type = "l", ylim = c(-40, 0), frame.plot = TRUE,
     ylab = "log-likelihood(\U03C0)", xlab = "\U03C0" )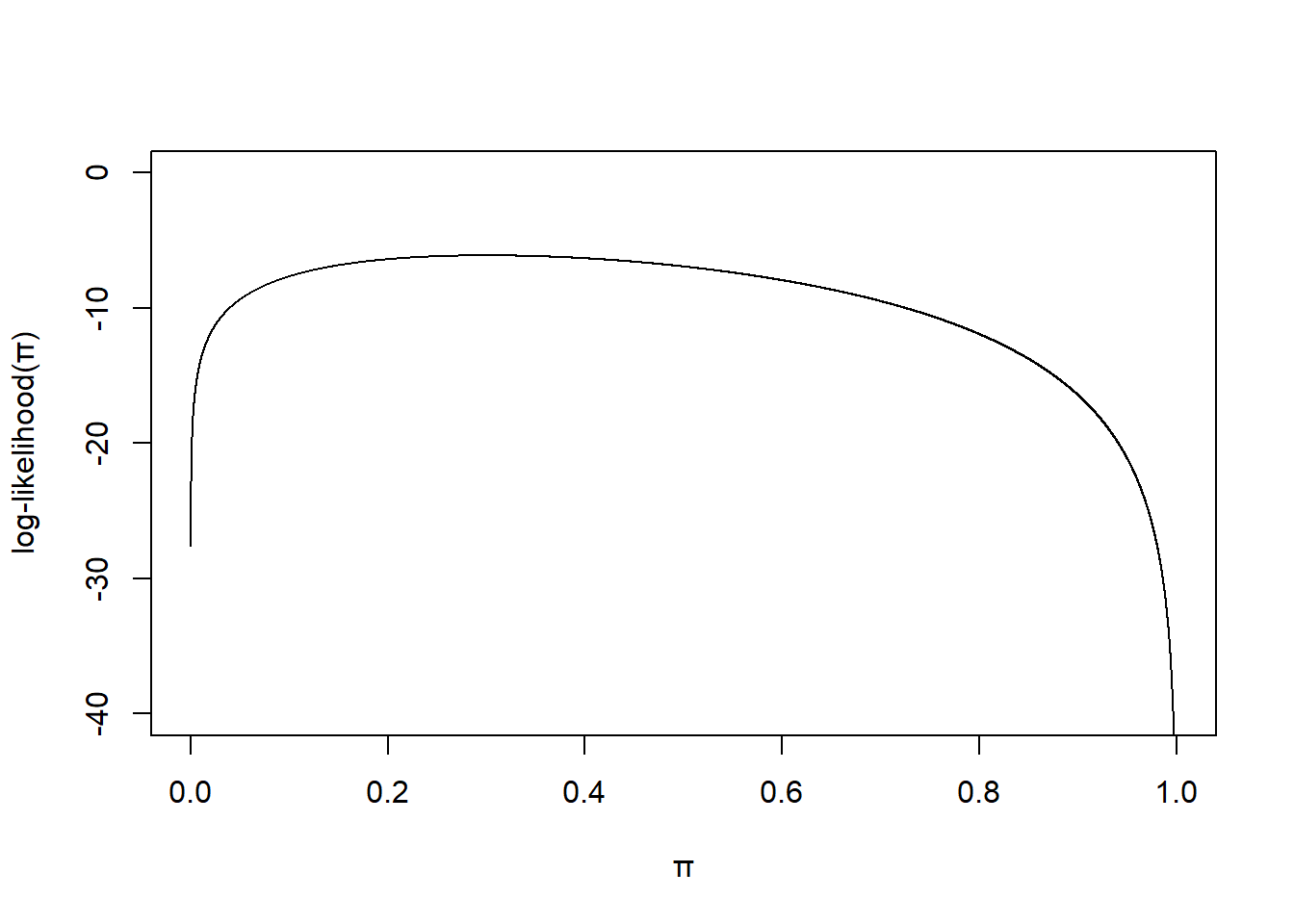

图 33.1: Log-likelihood for binomial model.

33.6.2.2 10名研究对象测量的总胆固醇浓度分别是 6.0, 6.2, 6.8, 5.3, 5.9, 6.1, 6.0, 7.0, 5.9, 6.3。已知人群中总胆固醇值服从方差为 4 (mmol/l)² 的正态分布。

对数似然方程是:

\[ \begin{aligned} \ell(\mu) & = -\frac{1}{2\times2^2}\sum_{i=1}^{10} (Y_i - \mu)^2 \\ & = -\frac{1}{8}\sum_{i=1}^{10} (Y_i - \bar{y} + \bar{y} - \mu)^2 \\ & = -\frac{1}{8}\sum_{i=1}^{10} (\bar{y} - \mu)^2 \\ & = -\frac{10}{8}(\bar{y} - \mu)^2 \end{aligned} \]

极大似然估计，和极大似然估计量是:

\[ \ell^\prime(\mu) = 0 \Rightarrow \hat\mu = \bar{y} = 6.15 \]

绘制对数似然方程的示意图

mu <- seq(5,7, by = 0.0001)
likelihood <- -(5/4)*(6.16-mu)^2
plot(mu, likelihood, type = "l", ylim = c(-1.8, 0), frame.plot = TRUE,
     ylab = "log-likelihood(\U03BC)", xlab = "\U03BC" )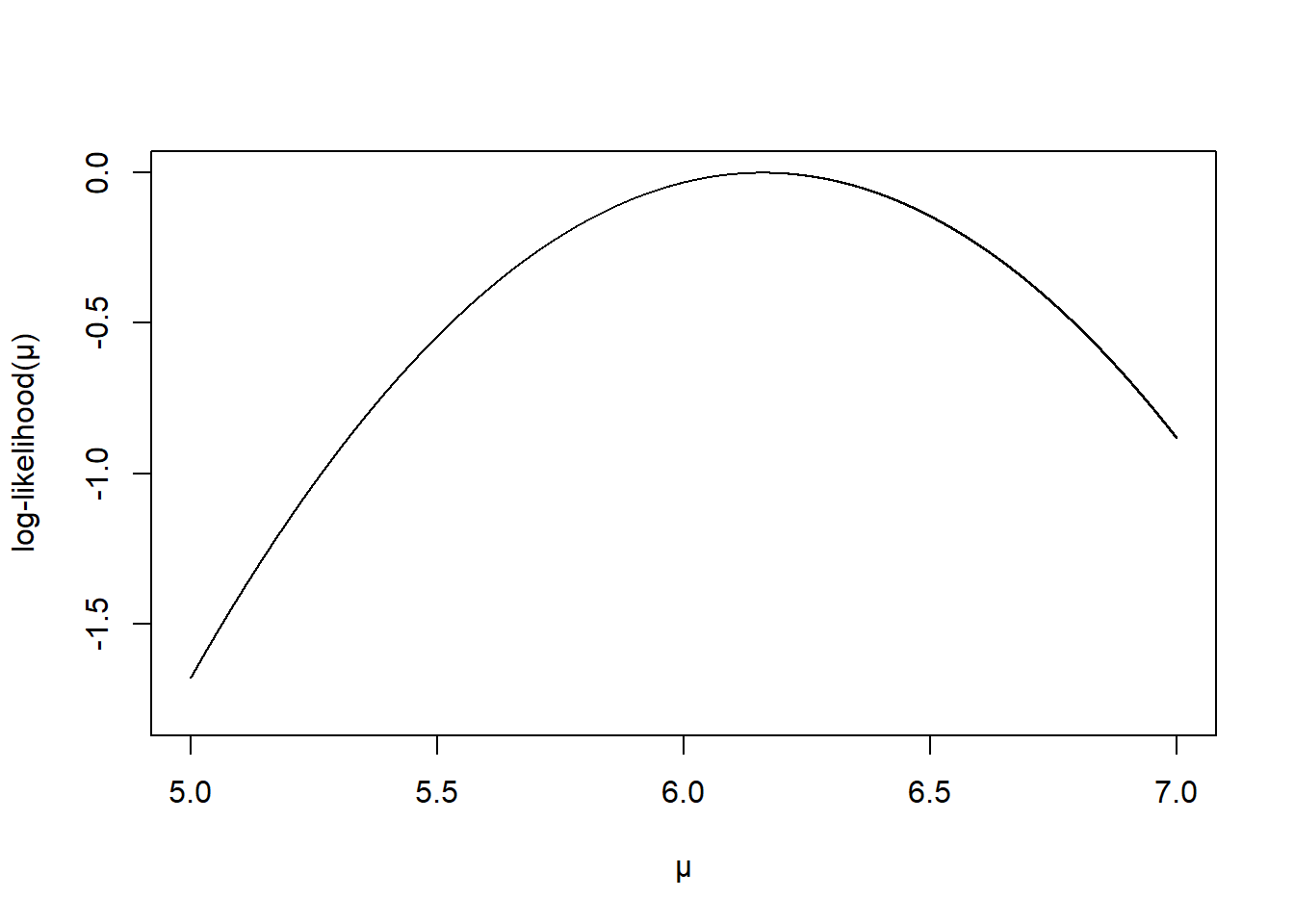

图 33.2: Log-likelihood for normal model

33.6.3 线性回归模型

某项RCT临床实验的目的是比较注射吗啡和安慰剂哪个对患者的精神医学指征的改变更加有效。每个实验组随机分配到24名患者，精神医学指征使用某种心理调查问卷，问卷有七道题，患者七道题的总得分被用于评价其精神医学指征，的分越高，指征越明显。下表是这两组患者在注射相应药物两小时之后答题的的分:

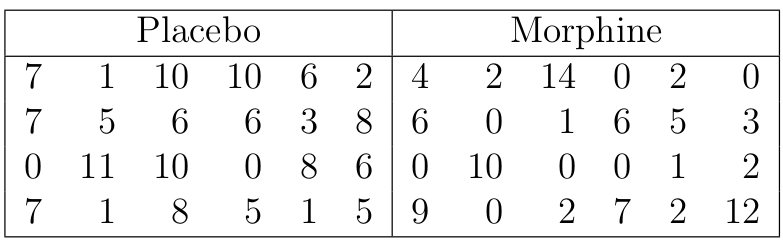
图 33.3: Mental activity scores recorded 2 hours after injection of the drug.

下面是 STATA 的计算结果，

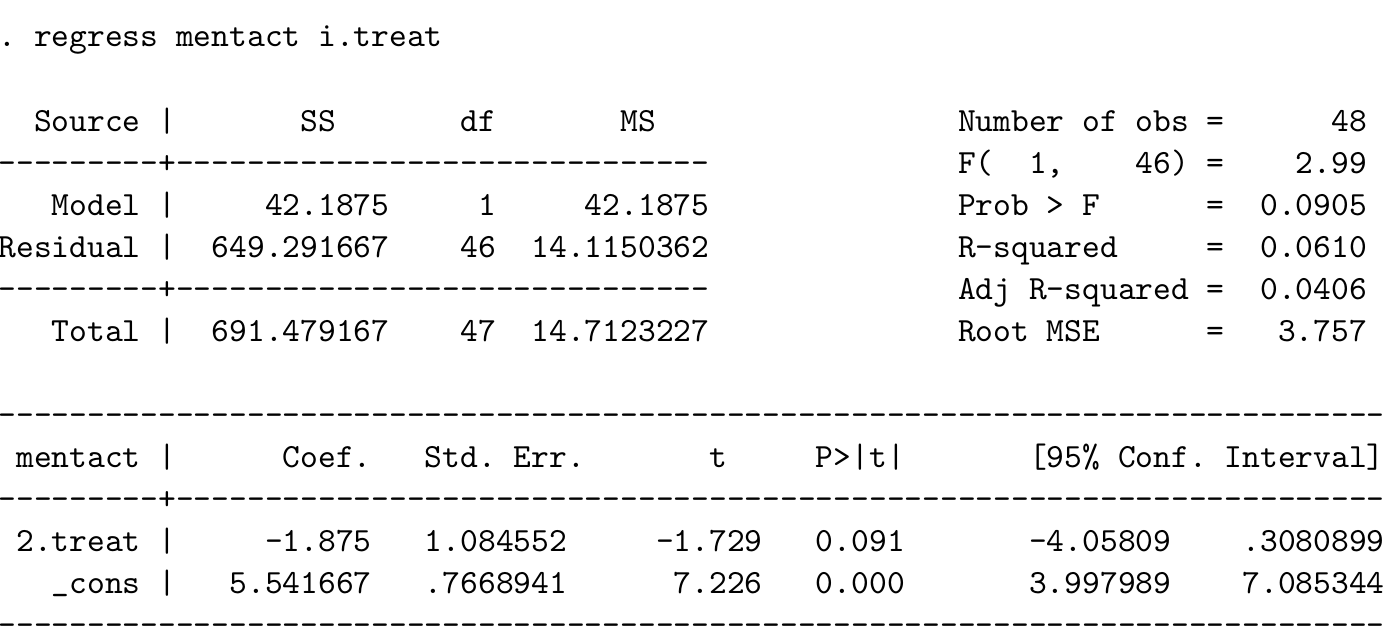
写下该模型的数学表达式，陈述该模型中用到的所有假设和前提条件。手动计算该简单线性回归模型的截距和斜率，确定你的结果和STATA的结果是一样的。

$Y_i$ 用来表示第 $i$ 名对象的精神医学指征问卷的得分。该模型可以写作:

$Y_1, Y_2, \cdots, Y_{48}$ 是 48 个独立同分布的随机变量，且 $Y_i \sim N(\mu, \sigma^2)$ \[ y_i = \alpha + \beta x_i \text{ for } x_i = \left\{ \begin{array}{ll} 0 \text{ placebo}\\ 1 \text{ morphine}\\ \end{array} \right . \]

从表格数据中可得$\bar{x} = 0.5, \sum x_i^2 = 24, \bar{y}=4.604, \sum x_iy_i=88$，利用之前33.5.3 复习的简单线性回归公式:

\[ \hat\alpha = 5.542 \\ \hat\beta = -1.875 \]

解释截距和斜率的实际意义:

$\hat\alpha$ 是安慰剂组的平均精神医学指征得分;
$\hat\beta$ 是注射吗啡组和安慰剂组两组之间得分均值之差。

实验研究同时还测量了两组在注射药物之前的精神医学指征得分，下面是在 STATA 里对该数据进行拟合的另一个模型。其中 prement 是药物注射前得分的变量:

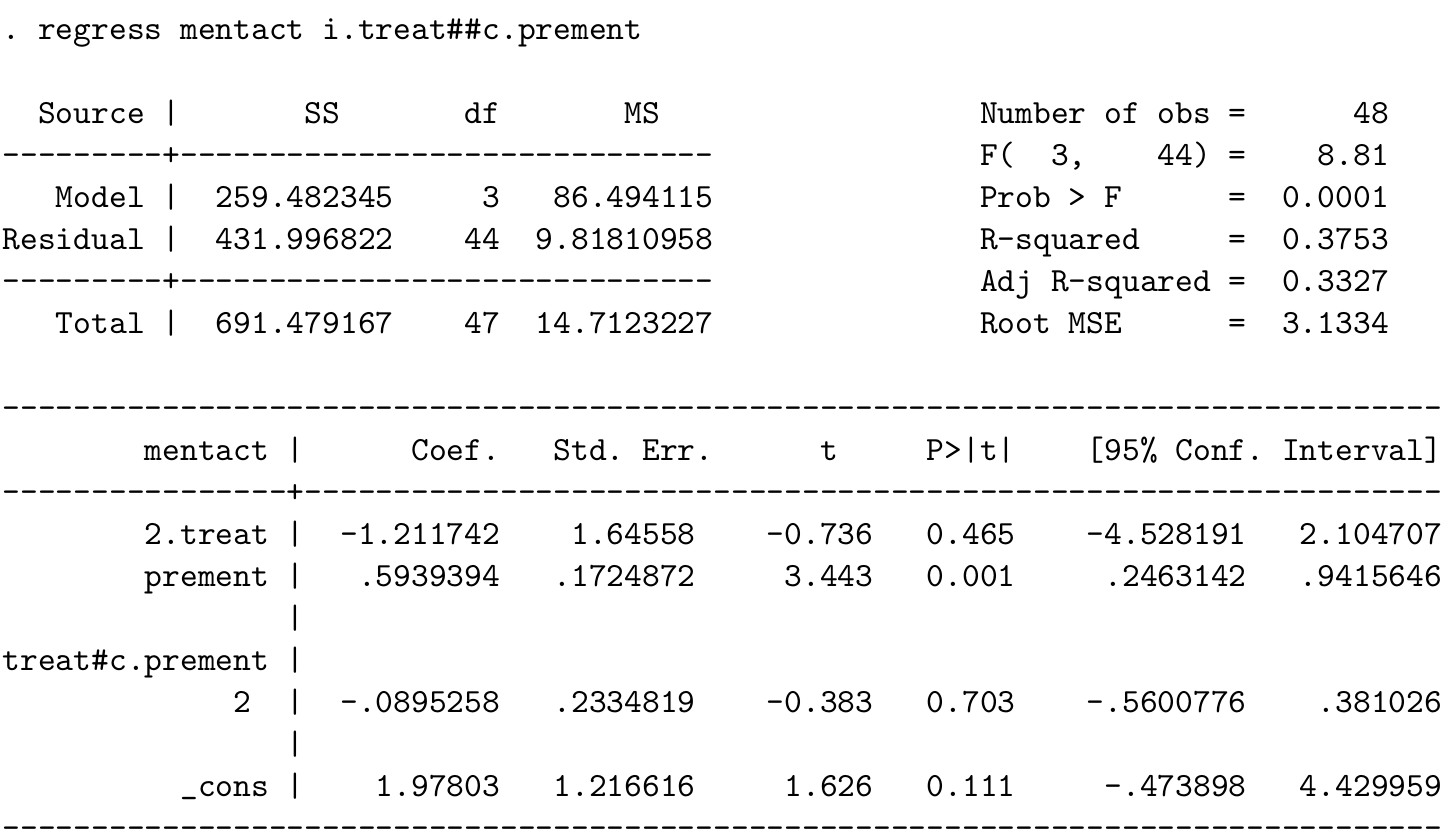
写下这个模型的数学表达式，并且解释你会用怎样的方法求各个参数的 MLE。

\[ y_i = \beta_0 + \beta_1 x_i + \beta_2 z_i + \beta_{12}x_iz_i \\ \text{ for } x_i = \left\{ \begin{array}{ll} 0 \text{ placebo}\\ 1 \text{ morphine}\\ \end{array} \right. \]

该模型的对数似然方程是

\[ \ell(\beta_0, \beta_1, \beta_2, \beta_{12} | \mathbf{y, z, x}) = -\frac{1}{2\sigma^2}\sum_{i=1}^ {48}(y_i - \beta_0 - \beta_1x_i - \beta_2z_i - \beta_{12}x_iz_i)^2 \]

把上面的对数似然方程等于零以后依次对 $\beta_0, \beta_1, \beta_2, \beta_{12}$ 求偏微分即可求得各自的 MLE。

解释各参数估计的实际意义

$\hat\beta_0 =$ _cons $=1.978$

是当且仅当治疗前得分为零时，模型对安慰剂组得分均值的估计; - $\hat\beta_1 =$ 2.treat $=-1.212$ 是当且仅当治疗前得分为零时，吗啡组和安慰剂组之间得分均值之差; - $\hat\beta_2 =$ prement $=0.594$ 是对照组中，治疗前得分每增加一个单位，治疗后得分的变化; - $\hat\beta_{12} =$ 2.treat#c.prement $=-0.0895$ 是吗啡组和安慰剂组两组之间回归斜率之差，也就是说\[\hat\beta_2 + \hat\beta_{12} = 0.505\] 是吗啡组中，治疗钱得分没增加一个单位，治疗后得分的变化。

33.6.4 似然比检验，Wald 检验，Score 检验

从服从正态分布 $N(\mu, 1)$ 的总体中抽样 $n$ 个样本，他们相互独立同分布 (i.i.d)。推导用这个模型时的三种检验方法的检验统计量，证明在此特殊情况下，三种检验方法的检验统计量完全一致。

该数据的对数似然是

\[ \ell(\mu) = -\frac{1}{2}\sum_{i=1}^n(y_i - \mu)^2 \]

似然比检验 likelihood ratio test

\[ \begin{aligned} -2llr & = -2(\ell(\mu_0 - \ell(\hat\mu))) \\ & = -2(-\frac{1}{2}\sum_{i=1}^n(y_i - \mu_0)^2 + \frac{1}{2}\sum_{i=1}^n( y_i - \bar{y})^2) \\ & = \sum_{i=1}^n[(y_i - \mu_0)^2 - (y_i - \bar{y})^2] \\ & = \sum_{i=1}^n(y_i^2 + \mu_0^2 - 2\mu_0y_i - y_i^2 - \bar{y}^2 + 2\bar{y}y_i) \\ & = n(\mu_0^2 - 2\mu_0\bar{y} + \bar{y}^2) \\ & = n(\bar{y} - \mu_0)^2 \end{aligned} \]

Wald 检验:

对数似然的一阶导数和二阶导数分别是:

\[ \ell^\prime = -\frac{1}{2}\sum_{i=1}^n-2(y_i-\mu) = \sum_{i=1}^n(y_i - \mu) \\ \ell^{\prime\prime} = -n \]

所以，Fisher information $S^2 = n^{-1}$，$M = \hat\mu = \bar{y}$，

\[ \begin{aligned} W^2 & = (\frac{M - \theta_0}{S})^2 \\ & = (\frac{(\bar{y} - \mu_0)^2}{n^{-1}}) \\ & = n(\bar{y} - \mu_0)^2 \end{aligned} \]

Score 检验

\[ \begin{aligned} \frac{\ell^\prime(\mu_0)^2}{-\ell^{\prime\prime}(\mu_0)} & = \frac{(n\bar{y} - n\mu_0)^2 }{n} \\ & = n(\bar{y} - \mu_0)^2 \end{aligned} \]

所以，在方差已知，均值未知，总体服从正态分布的数据条件下，三种检验方法获得的实际检验统计量是完全一致的。

R语言与医学统计

第 33 章重要概念回顾

33.1 概率论统计推断要点

33.2 似然

33.3 极大似然估计