第 28 章 线性回归的模型诊断

和其他的统计学模型一样，线性回归也有自己的前提条件，而且从模型结果作出的各种推断都依赖这些前提条件的成立。所以，我们需要有一些统计学的手段来检查线性回归模型中这些前提是否得到满足。然而理想总是很丰满，现实通常又太骨感。你不大可能找到一组真实的数据能够 100% 完美的满足所需要的前提条件。当然不是说不能满足模型的前提条件，我们就无法进行统计推断了。而且我们也有不少结果稳健 (robust) 的统计学手段，让我们可以不必考虑太多前提条件。检查数据，了解数据内容，理解数据本身的结构永远都是有助于数据分析的。

还要记得一点就是，根据中心极限定理，(即使有一些前提假设不能成立) 大型数据分析结果的稳健性/可靠性，要高于小型数据的分析。

28.1 线性回归模型的前提条件

  1. 因变量和各个预测变量之间的关系都是线性 linear relationship 的；
  2. 因变量之间相互独立；
  3. 真实 true 残差的方差是恒定不变的(constant)。这里的含义是在真实回归直线上下散布的因变量的点，在任意一个预测变量值的位置的方差 (分散) 要保持恒定不变。这个特性被描述成方差齐性 homoscedasticity (残差方差的一致性 homogeneity of the residual variance)，与之相对的定义是异方差性 heteroscedasticity (残差方差的不同质性，heterogeneity of the residual variance)。
  4. 真实残差服从正态分布。 (尽管R统计包里丢入随便什么数据都能给你个线性回归的报告来，但是，如果你真想用其结果做统计推断，p CI 的话，这条前提必须满足。)

本章着重讨论第 1，3，4 前提条件的诊断法。因为观测数据之间是否独立性 (第 2 条)并不是你光盯着数据看就能知道的。

28.2 用图形来视觉诊断

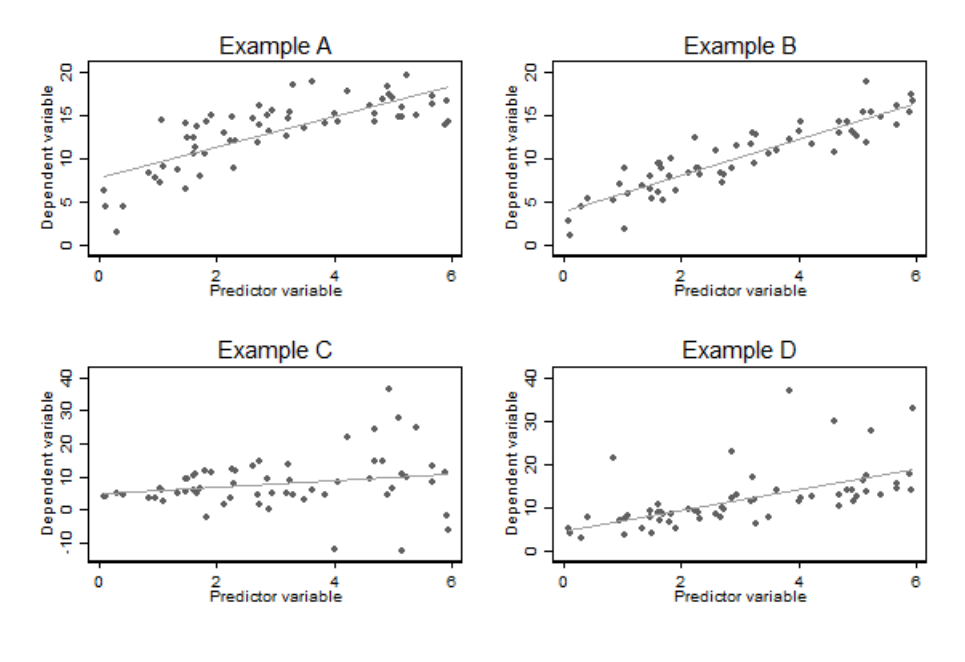
Illustration the usefullness of scatter plots of the dependent variable against the predictor variable in simple linear regression

图 28.1: Illustration the usefullness of scatter plots of the dependent variable against the predictor variable in simple linear regression

图 28.1 中展示了四种实例。把预测变量和因变量做散点图，这常常是甄别出异方差性 (Example C)，非线性 (Example A)，异常值 (Example D) 的最好方法。其中右上角的 Example B 是良好的回归模型的散点图应该有的样子。

建议进行视觉判断的时候把拟合曲线去掉再作一次，看看有回归直线和没有回归直线前后的散点图差别，更容易看出数据的分布特征。但是光看散点图作判断的方法，在多元线性回归模型中只能看看能否找到一些异常值，对辅助判断方差齐性和线性关系就没有太大的用处。残差点图就更加实用。

28.3 残差图

如果线性回归模型的前提条件能够得到满足，那么拟合模型后的残差，一定会服从正态分布且方差均匀一致。所以另一个诊断异方差性的办法可以通过作观察残差和拟合值之间的散点图来辅助判断。下图 28.2 是各个简单线性回归拟合后的残差和拟合值之间的散点图。可以看出左下角的 Example C 的异方差性展现得更加明显了。同样此图也能帮助判断线性关系，如左上角的 Example A 所示，如果预测变量和因变量之间不是线性关系，那么残差就不可能均匀的分布在 \(0\) 的两侧。

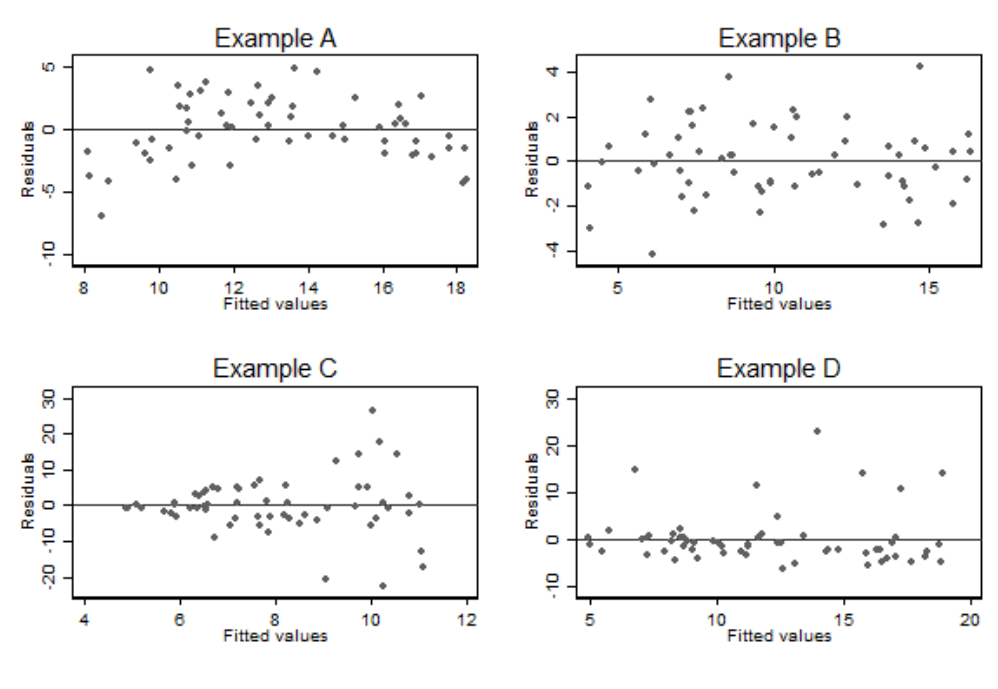
Plots of residuals agianst fitted values for the examples in the previous figure

图 28.2: Plots of residuals agianst fitted values for the examples in the previous figure

对于一个简单线性回归模型来说，拟合值仅仅只是预测变量的一个线性数学转换，所以上面图中的残差和拟合值的散点图，其实等价于残差和预测变量的散点图。所以图 28.1 和图 28.2 两图展现的信息量此时是一样的。

但是，多元线性回归时，残差和拟合值的散点图会比残差和预测变量散点图更适合判断异方差性，和线性关系的假设。

28.4 残差正态图

正态图在分析技巧的章节也有介绍 (Section 22.2.1)。这是最佳的判断数据是否服从正态分布的视觉图。所以用它来绘制线性回归拟合后的残差，是个很好的办法。可惜的是残差正态图无法用于判断异方差性，和线性关系两个假设。

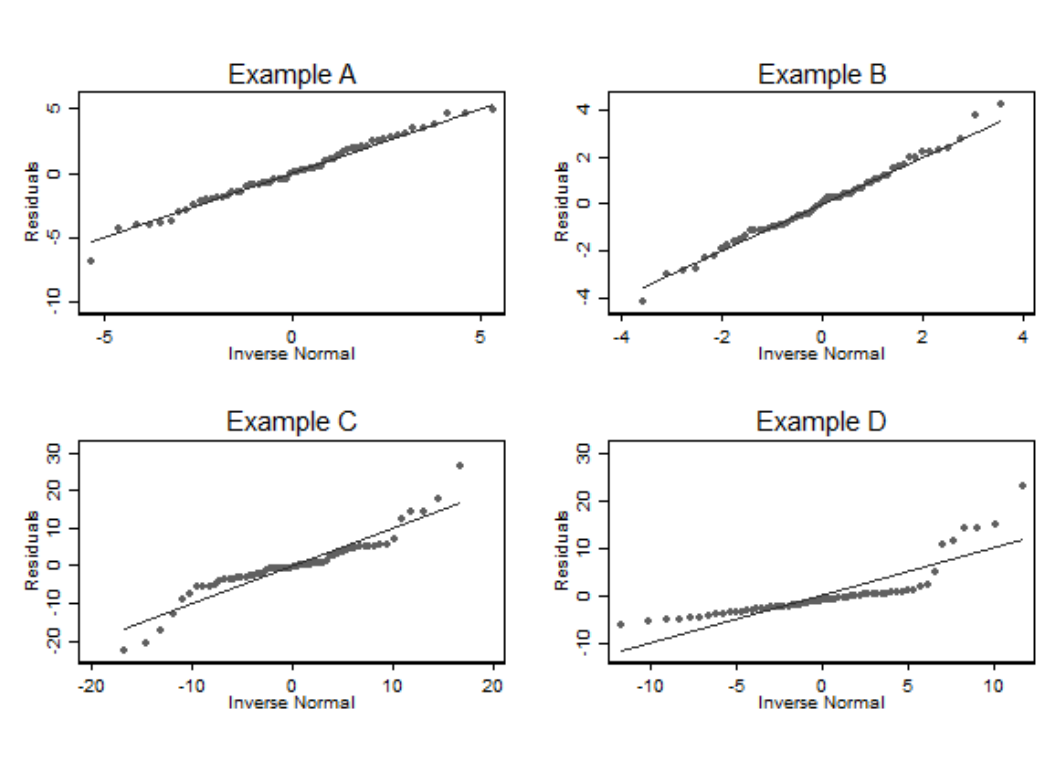
Normal plots of residuals for the examples in the previous figure

图 28.3: Normal plots of residuals for the examples in the previous figure

有时后观察残差 (observed residuals) 可能不能满足齐方差性质而真实残差 (true residuals) 反而满足。所以一些统计学家建议把计算的残差标准化 (standardised residuals) 以后再作正态图。

28.4.1 模型诊断实例

前面建立过的儿童体重和年龄，身长之间的多元回归模型的诊断 (Section 27.3.3) 见下图。所有四个图都没有证据证明非线性关系和异方差性。看不见显著的异常值。正态图看出残差有那么一点点不太正态分布，但是不严重到让人怀疑模型给出的推断是否受到重大影响。

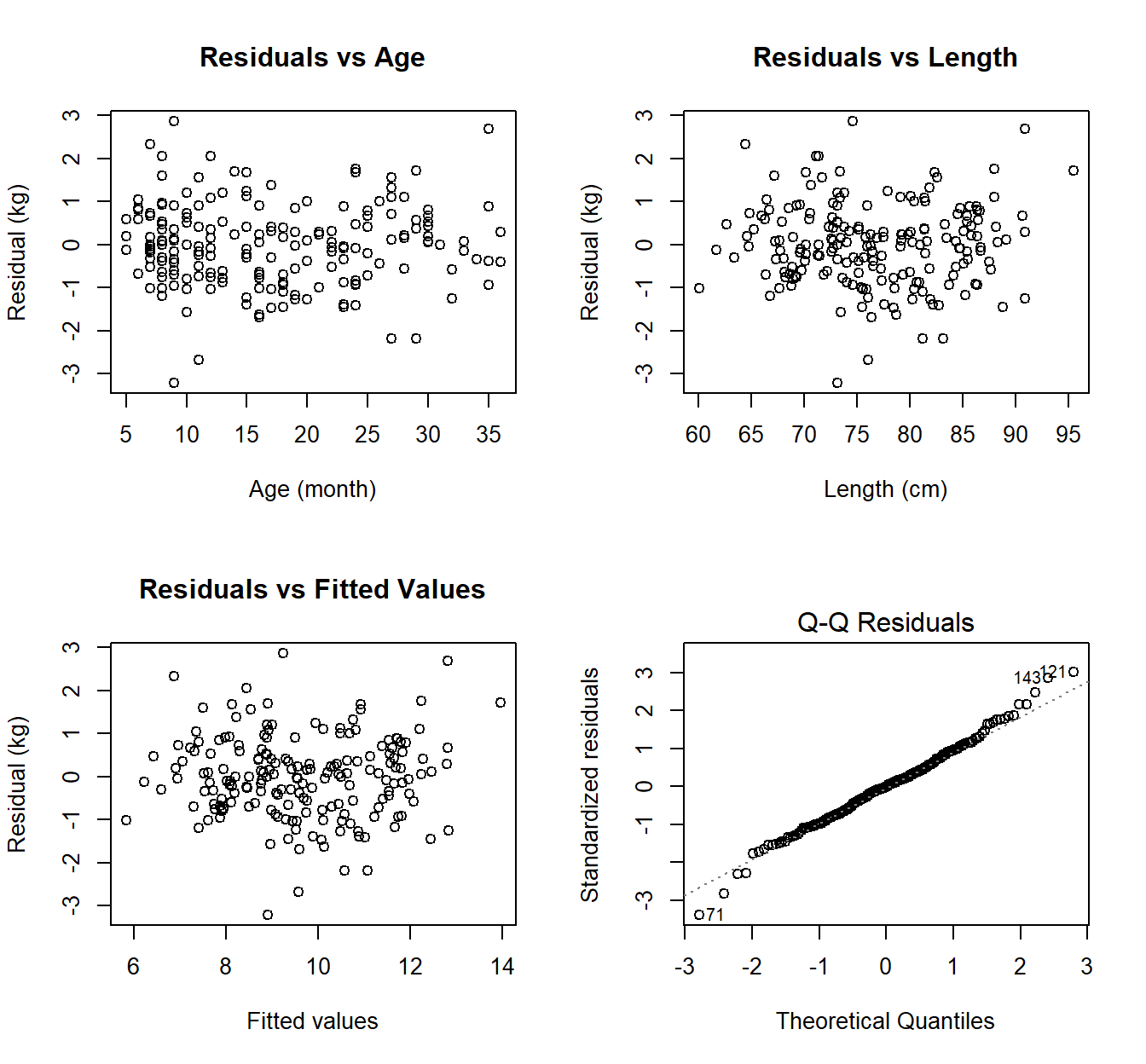
Residual plots for the linear regression relating a child's weight to their age and length

图 28.4: Residual plots for the linear regression relating a child’s weight to their age and length

28.5 前提条件的统计学检验

28.5.1 二次方程回归法检验非线性

二次方程回归法是一种多元回归模型，它包含了两个预测变量，一个是另一个的平方。数学模型可以标记成为：

\[ \begin{aligned} y_i & = \alpha + \beta_1 x_i + \beta_2 x_i^2 + \varepsilon_i \\ \text{Where } & \varepsilon_i \sim \text{NID}(0, \sigma^2) \end{aligned} \tag{28.1} \]

尽管你看到了二次方程在这里，但是这仍然是一个线性回归模型。但是二次方程的回归模型描述的是 \(Y, X\) 两个变量之间的非线性关系。如果你把方程\(\hat{y}_i = \hat\alpha + \hat\beta_1x_i + \hat\beta_2x^2_i\) 对\(x_i\) 求微分，你会得到\(\hat\beta_1+2\hat\beta_2 x_i\)。这是二次方程的曲率方程。所以如果结果中报告 \(\hat\beta_2\) 是有统计学意义的，就等于是有证据证明这两个变量之间的关系不是线性的。

growgam1$age2 <- (growgam1$age)^2
Model2 <- lm(wt ~ len + age + age2, data=growgam1)
print(summary(Model1), digits = 5)
## 
## Call:
## lm(formula = wt ~ age + len, data = growgam1)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -3.20525 -0.64402 -0.00303  0.55967  2.86277 
## 
## Coefficients:
##              Estimate Std. Error t value  Pr(>|t|)    
## (Intercept) -8.351244   1.259968 -6.6281 3.531e-10 ***
## age         -0.011260   0.016751 -0.6722    0.5023    
## len          0.237129   0.019516 12.1502 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.95456 on 187 degrees of freedom
## Multiple R-squared:  0.74337,    Adjusted R-squared:  0.74063 
## F-statistic: 270.84 on 2 and 187 DF,  p-value: < 2.22e-16
print(summary(Model2), digits = 5)
## 
## Call:
## lm(formula = wt ~ len + age + age2, data = growgam1)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -3.30561 -0.64811 -0.01615  0.54829  2.74233 
## 
## Coefficients:
##               Estimate Std. Error t value  Pr(>|t|)    
## (Intercept) -8.5918429  1.2537775 -6.8528 1.031e-10 ***
## len          0.2514685  0.0205039 12.2644 < 2.2e-16 ***
## age         -0.1110198  0.0502050 -2.2113   0.02823 *  
## age2         0.0023351  0.0011091  2.1055   0.03659 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.94592 on 186 degrees of freedom
## Multiple R-squared:  0.74935,    Adjusted R-squared:  0.74531 
## F-statistic: 185.36 on 3 and 186 DF,  p-value: < 2.22e-16

正如上面的二次方程模型输出结果所示，年龄和体重之间，当调整了身高以后，有证据 (但是较弱) 证明不呈现线性关系 \((p=0.037)\)。

28.5.2 非线性关系模型

二次方程的回归模型的应用在非线性模型中的应用其实有许许多多的缺陷。例如二次方程回归只能默认有一个极致点。也就是在二次方程模型中，预测变量和因变量的关系要么是先下降后升高，要么是先升高再下降。不光如此，二次方程回归还默认二者之间的关系在极致点是左右对称的。这无论如何在现实中都很难有成这样关系的两个变量。所以，假如你使用二次方程模型回归之后发现非线性的证据是有意义的，那么更好的办法是接下来拟合一个更加符合实际情况的非线性模型-多项式曲线回归模型。

二次方程回顾模型是多项式曲线回归模型的最简单形式，其次是三次方程模型 (其实就是在公式 (28.1) 里面加一个 \(+\beta_3 x_i^3\))。另一种更加灵活的模型是拟合一个精确的分段式多项式模型，即允许在不同范围 (被描述为 “结点 knots”) 的预测变量 \(X\) 内拟合不同的模型。其中一种叫做 限制性立方曲线模型 restricted cubic spline model (点这里看我用了这种方法的论文)：

  1. 默认第一个节点之前和最后一个节点以后为直线模型；
  2. 其余节点之间默认用三次方回归模型拟合数据；
  3. 在节点处的两个方程之间用平滑的曲线连接 (强制两个方程的一阶二阶导数相等即可 constraining the first and second derivatives of adjacent functions to agree when they meet at the knot point)

28.6 异常值，杠杆值，和库克距离

观测值中的异常值很显然对模型的拟合会有较大的影响。如果某个观测值对应的拟合值是异常值的话，那么这样的值被认为杠杆值很大。库克距离 (Cook’s Distance) 是另一种用来衡量异常值的手段。

28.6.1 异常值和标准化残差

异常值指的是那些通过模型拟合过后，观测值和拟合值差异很大的那些观察对象。这些值需要被甄别出来因为它们

  1. 可能是数据录入阶段造成的人为失误，或者是有什么别的原因导致的系统性异常需要让输入数据的人员进行进一步的调查；
  2. 异常值可能较大的影响回归系数的方差估计，造成不精确甚至错误的结果；
  3. 异常值也会影响回归系数本身的估计。

观测值和拟合值之间的差，被命名为观测残差 (observed residuals)。线性回归模型的前提之一是 真实残差 独立且方差维持恒定不变。但是观测残差却无可能做到独立且方差恒定不变。

之所以说观测残差不是独立的，可以这样来理解：假如拟合某个线性回归模型，预测变量是二分类的，且其中一个分类只有两个观测值，那么拟合的直线会通过这两个观测值的中心点(均值)，那么这两个观测值的观测残差就恰好分布在回归直线的两侧(相加之和为零，呈完美负相关)，它们是**相关的* *！ ！ ！

观测残差的方差不可能恒定的理由，可以这样来理解：同样假如拟合某个预测变量是二分类的线性回归模型，其中一个分类只有一个观测值，那么回归直线在这个观测值处的残差方差是零。

标准化残差 (standardized residuals) \((r_i)\)，被定义为每个观测值的残差和模型估计的残差标准误相除获得的数据。所以符合前提条件的线性模型拟合后，计算的标准化残差会服从标准正态分布。从标准正态分布的知识你也应该知道，\(95\%\) 的观测值的标准化残差必须分布在数值 \(-2, 2\) 范围内。另外一种标准化残差的方法叫做内学生化残差 (studentised residual)。内学生化残差是把观测值的残差除以每一个观测值各自的估计标准误。在 R 里面可以通过 rstandard() 命令计算回归模型每个观测值的内学生化残差。 内学生化残差也是服从标准正态分布的。

28.6.2 杠杆值

如果一个观测值的拟合值十分极端，那么该观测值本身可能对回归模型的参数估计影响很大。这个影响程度大小用杠杆值 (Leverage)衡量。简单线性回归时，每个观测值的杠杆值计算公式为：

\[ \begin{aligned} l_i = \frac{1}{n} + \frac{x_i-\bar{x}}{SS_{xx}} \end{aligned} \tag{28.2} \]

杠杆值的范围是 \(\frac{1}{n}, 1\) 之间。杠杆值方程提示这是一个单调函数，它是评价预测变量本身到该变量均值之间距离的指标。杠杆值越大，该观测值就有越大的可能性对模型拟合造成影响。如果杠杆值大到等于 \(1\)，那么杠杆效应造成的影响极大，观测值和拟合值就完全一致。意味着在这个观测值附近，只有它自己，没有其他观测值。

多元线性回归时的杠杆值计算公式和 (27.7) 中的帽子矩阵 \(\mathbf{P}\) 有关：

\[ \begin{aligned} & l_i = \mathbf{P}_{ii} \text{ The } i\text{ th diagonal element of } \\ & \mathbf{X(X^\prime X)^{-1}X^\prime} \end{aligned} \tag{28.3} \]

In multiple regression, leverage measures “distance” from the centre of the joint distribution of the predecitor variables, but with distance scaled by the directional degree of dispersion. Notice that the point with largest leverage would not have particularly high leverage in either simple linear regression models including only one of the two (or more) predictor variables. Further this point would not be readily identified in plots of each of the predictor variables against the dependent variable. The value of measures such as the leverage is greatest in complex multiple regression models where it can be difficult to identify points with an atypical combination of predictor variables using more simple graphical techniques.

28.6.3 库克距离

当通过计算观测值的杠杆值之后，发现具有较大杠杆值的那些观测点，应该被视为对模型的稳定性有“潜在威胁”。此时就轮到库克距离 (Cook’s Distance)的登场。库克距离可以用来衡量一个观测值对模型的影响大小 (比较把观测值移除出模型前后的模型变化)。

对于一个有\(p\) 个预测变量的回归模型来说，如果残差方差的估计值为\(\hat\sigma^2\)，那么第\(i\) 个观测值的库克距离的计算过程就是把该观测值移除，重新拟合相同的模型，计算获得该点做的新的拟合值\(\hat y_{j(i)}\)：

\[ \begin{aligned} D_i = \frac{\sum^n_{j=1}(\hat y_{j(i)} - \hat y_j)^2}{(p+1)\hat\sigma^2} \end{aligned} \tag{28.4} \]

可以被证明的是，库克距离其实是结合标准化残差值 \((r_i)\)，和杠杆值 \((l_i)\) 的一个综合量：

\[ \begin{aligned} D_i & = \frac{\sum^n_{j=1}(\hat y_{j(i)} - \hat y_j)^2}{(p+1)\hat\sigma^2} \\ & = \frac{r^2_il_i}{(p+1)(1-l_i)} \end{aligned} \tag{28.5} \]

所以从库克距离和标准化残差，以及杠杆值之间的关系公式(28.5) 也可以看出，当杠杆值大同时标准化残差值的绝对值也大的观测值，库克距离就会很大。用线性回归时，把每个观测值得库克距离和拟合值作散点图，或者把杠杆值和标准化残差作散点图是常用的判断异常值的手段。

28.7 利用R对模型诊断作图

拟合好了一个线性回归模型以后，plot(Modelname) 即可看到四个诊断图 (Section 23.8.4)。