第 19 章 假设检验

19.1 抛硬币的例子

对数据进行假设检验是统计分析最重要的部分。一般进行实验或者调查时我们会先设定一个零假设。假如实验或者调查中获得的一系列数据可以认为是相互独立且随机地从人群中抽取的样本，那么根据零假设为真的条件，样本数据提供的参数估计和零假设条件下的参数应该是差距不大(一致) 的。因为概率论环境下，我们用样本数据来作假设检验，如果样本提供的数值比起零假设条件下的参数大很多或者小很多，我们就有理由，有证据拒绝零假设。

下面用投硬币作为例子说明。硬币如果是公平的，那么抛硬币后正反面出现的概率应该一样，都是 \(50\%\) (零假设：\(p=0.5\))。假如有一枚硬币，抛了\(10\) 次只有一次是反面朝上的，我们可能就会怀疑，这枚资本主义硬币一定是被做了手脚(变得不再公平了)，这就是通过实验质疑和挑战零假设的思想。如此粗糙的想法却是统计学假设检验的理论起源。只是在统计学里面，需要制定一些规则来规定，实验数据跟零假设 (设想) 差异达到多大时 (检验)，认为证据足够达到相信零假设“非真” (挑战权威)。

检验的过程，就是计算我们朝思暮想的 \(p\) 值。 \(p\) 值的定义是，当零假设为真时，我们观察到的实验结果以及比这个结果更加极端 (双侧) 的情况在所有可能的情况中出现的概率。继续使用抛硬币的例子来说的话，跟 “\(10\) 次抛硬币出现一次反面朝上” 一样极端或者更加极端的事件有：

  • “一次反面朝上”，
  • “零次反面朝上”，
  • “九次反面朝上 (或者说一次正面朝上)”，
  • “十次反面朝上 (或者说零次正面朝上)”。

相反地，没有观察事件 “\(10\) 次抛硬币出现一次反面朝上” 那么极端的事件就包括了：

  • “两次反面朝上”，
  • “三次反面朝上”，
  • “四次反面朝上”，
  • “五次反面朝上”，
  • “六次反面朝上”，
  • “七次反面朝上”，
  • “八次反面朝上”。

检验的过程我们会定义一个被检验的统计量，一般就是我们感兴趣的参数的估计 (estimator of a parameter of interest)。在上面抛硬币的例子中，这个检验统计量就是 “硬币反面朝上的次数”。观察到的反面朝上次数除以抛硬币次数 (\(10\) 次) 就是获得硬币反面朝上的概率 (参数) 的估计。用\(R\) 表示十次抛硬币中观察到反面朝上的次数，那么此时\(R\) 就是一个服从二项分布的随机变量，其服从的二项分布成功(反面朝上事件发生) 的概率(参数) 是\(\pi\)。所以某一次实验中 (抛十次硬币算一次实验)，\(R=r\)，那么这次试验的参数估计的 \(p\) 值被定义为：

\[ \begin{equation} \text{Prob}\{ R \text{ as or more extreme than } r | \pi=0.5 \} \end{equation} \tag{19.1} \]

零假设：反面朝上出现的概率是 \(\pi=0.5\)；替代假设： \(\pi\neq 0.5\)。当零假设为真时，\(R\sim \text{Bin}(10, 0.5)\)，它的零假设分布如下图 19.1：

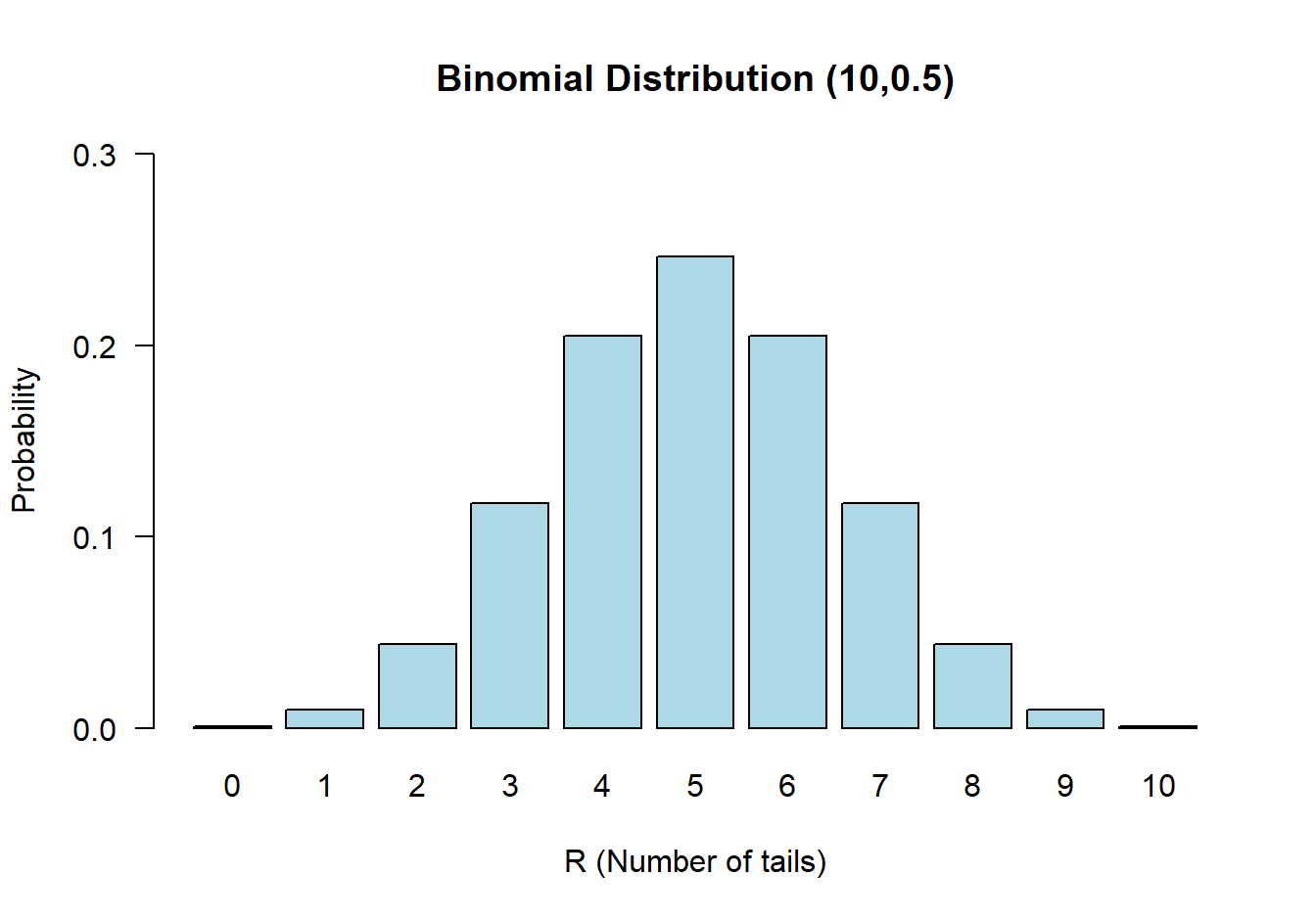
Binomial distribution n=10, π = 0.5

图 19.1: Binomial distribution n=10, π = 0.5

本节抛硬币的例子我们观察到十次抛硬币只有一次反面朝上，\(r=1\)。其发生的概率等于上面列举的四种与之同等极端或者更加极端的情况发生概率之和：

\[ \begin{aligned} &\text{Prob} \{R=0|\pi=0.5\} + \text{Prob} \{R=1|\pi=0.5\} + \text{Prob} \{R=9|\pi =0.5\} + \text{Prob} \{R=10|\pi=0.5\} \\ & = (\binom{10}{0} + \binom{10}{1} + \binom{10}{9} + \binom{10}{10})\times(0.5)^{10} = 0.021 \end{aligned} \]

19.1.1 单侧和双侧检验

在上面的例子中其实我们已经用到了双侧检验的概念。例如，我们把“九次反面朝上” 事件发生的概率当作和“一次反面朝上” 事件发生的概率具有同等“极端”概率事件，但是其实在图19.1中也能看出两种事件发生的方向是在概率分布的左右两侧，这就是典型的双侧检验思想。一个“单侧”检验则不考虑另一个方向发生的极端事件。

还是用本节的例子，如果要计算单侧检验 \(p\) 值：

\[ \begin{aligned} &\text{Prob}\{R\leqslant r| \pi=0.5\}\\ &\text{In the example } r=1 \\ &\Rightarrow \text{Prob}\{R=0 | \pi = 0.5\} + \text{Prob}\{ R=1 | \pi = 0.5 \} = 0.011 \end{aligned} \]

此时零假设为 \(\pi=0.5\)，替代假设为 \(\pi < 0.5\)。

大多数时候，单侧检验的 \(p\) 值十分接近双侧检验 \(p\) 值的一半。但是实施单侧假设检验的前提是，我们有绝对的把握事件不会发生另一个方向上，但是这种情况少之又少，所以基本上你能看到的绝大多数假设检验计算的\(p\) 值都是双侧检验\(p\) 值。

19.1.2 \(p\) 值的意义

假设检验被认为是作决策的一种手段。你会看到一些人使用 \(0.05\) 作阈值来作为拒绝 (\(<0.05\)) 或接受 (\(>0.05\)) 零假设的依据。许多医学实验，医学研究的结果确实是用来作决策的依据。例如某个临床试验用随机双盲对照实验法比较新药物和已有药物对某种疾病的治疗效果差异，通过实验结果来决定是否向市场和患者推广新的治疗药物，此时\(p\) 值的大小就是作决断的重大依据。然而还有另外的很多实验/研究并非为了作什么直接的决策，可能只是为了更多的了解疾病发生的原因和机制。例如可能乳腺癌多发在女性少发在男性人群，这显然是十分显著的差异，但是这种结果不能让我们决策说要不要改变一个人的性别，而只是提供了疾病发生发展过程的机理上的证据。因此，许多研究者主张把 \(p\) 值大小当作是反对零假设证据的强弱指标。但是此处要指出的是，并非所有统计学家都认同 \(p\) 值大小真的可以度量证据的强弱水平。

所以，建议在写论文，作报告时，尽量避免说：“本次实验研究结果具有显著的统计学意义，there was evidence that the result was statistically significant”。建议使用的语言类似这样：“在显著性水平为5% 时，本研究结果达到了统计学意义，statistically significant at the 5% level”；或者“在显著性水平为5% 时，我们的研究提供了足够的证据证明零假设是不正确的，there was evidence that at the 5% level, that the hypothesis being tested was incorrect”。

如果一个实验结果 \(p\) 值大于 0.05，可以被解读为：实验结果不能提供足够的证据证明零假设是错误的，there was no (or insufficient) evidence against the null hypothesis。另外还有一些人会使用一些词语来描述\(p\) 值大小：如果\(p=0.0001\)，可能会被解读为实验提供了“强有力的证据”，反对零假设；如果\(p=0.06; p =0.04\)，会被人解读为是具有“临界统计学意义，borderline statistically significant”，或者试验结果提供了“一些证据，some evidence” 反对零假设。

19.1.3 \(p\) 值和置信区间的关系

总体参数 \(\mu\) 如果真的被我们计算的估计值的 \(95\%\) 置信区间所包含，那么 \(p > 0.05\)。如果参数 \(\mu\) 不被计算的 \(95\%\) 置信区间所包含，那么 \(p < 0.05\)。

19.2 二项分布的精确假设检验

若\(n\) 次实验中成功次数为\(R\)，那么样本百分比(估计，estimator) \(P=\frac{R}{n}\) 是它的人群比例\(\pi\) (参数，parameter) 的无偏估计。欲检验的零假设\(\pi=\pi_0\)，替代假设\(\pi\neq\pi_0\)，且某一次观察结果为\(R=r\)，我们要计算的\(p\) 值就是在零假设条件下，所有情况中\(R=r\) 或者与之同等极端甚至更加极端的事件所占的比例。

  • 如果 \(r<n\pi_0\)，单侧 \(p\) 值等于

\[ \begin{aligned} p & = \text{Prob}\{ \text{r or fewer successes out of n | }\pi=\pi_0\} \\ & = P_0 + P_1 + P_2 + \cdots + P_r \\ \text{Where } & P_x = \binom{n}{x} \pi_0^x (1-\pi_0)^{n-x} \end{aligned} \]

  • 如果 \(r>n\pi_0\)，单侧 \(p\) 值等于

\[ \begin{aligned} p & = \text{Prob}\{ \text{r or more successes out of n |} \pi=\pi_0 \} \\ & = P_r + P_{r+1} + P_{r+2} + \cdots + P_{n} \\ \text{Where } & P_x = \binom{n}{x} \pi_0^x (1-\pi_0)^{n-x} \end{aligned} \]

一般情况下两个单侧 \(p\) 值很接近，所以双侧 \(p\) 值就可以计算其中一个然后乘以 \(2\)。你也可以计算两侧的单侧 \(p\) 值然后相加。

当样本量较大：

如果样本量 \(n\) 比较大，那么计算上面的精确法是十分繁琐的 (计算器也会累。。。)。可以考虑利用中心极限定理用正态近似法进行假设检验。此时需要做的就是把近似后的正态分布标准化，然后和标准正态分布做比较获得 \(p\) 值即可：

\[ \begin{equation} Z=\frac{R-E(R)}{\sqrt{\text{Var}(R)}} = \frac{R-E(R)}{\text{SE}(R)} \end{equation} \tag{19.2} \]

在目前为止人类所知道的范围内，上面公式的 \(Z\) 值随着实验样本量 \(n\) 的增加而无限接近标准正态分布 \(N(0,1)\)。

19.3 二项分布的正态近似法假设检验

二项分布的特征值：

\[ E(R) = n\pi_0; \text{ and Var}(R) = n\pi_0(1-\pi_0) \]

套用公式 (19.2)，计算 \(Z\) 值如下：

\[ \begin{aligned} Z & = \frac{R-E(R)}{\sqrt{\text{Var}(R)}} \\ & = \frac{R-n\pi_0}{\sqrt{n\pi_0(1-\pi_0)}} \\ & = \frac{P-\pi_0}{\sqrt{\frac{\pi_0(1-\pi_0)}{n}}} \\ \text{Where } & P=\frac{R}{n} \end{aligned} \]

利用实验数据的\(p=r/n\)，以及零假设时的\(\pi_0\)，就可以计算上面的观察\(Z\) 值，之后查阅标准正态分布的概率表格就可以获得单侧\(p\)值，别忘了乘以\(2\)。

19.3.1 连续性校正

连续性校正 (continuity correction):

在使用正态分布近似法进行二项分布数据的假设检验时，我们其实是在使用一个连续型分布近似一个离散型分布，误差通常会比较大。我们会使用矫正后的正态近似法计算 \(Z\) 值：

\[ Z=\frac{|R-n\pi_0|-\frac{1}{2}}{\sqrt{n\pi_0(1-\pi_0)}} \text{ or } Z=\frac{|P-\pi_0 |-\frac{1}{2n}}{\sqrt{\frac{\pi_0(1-\pi_0)}{n}}} \]

“Statistical Methods in Medical Research”(Armitage, Berry, and Matthews 2008)书中建议，满足\(n\pi \geqslant 10 \text{ or } n(1-\pi) \geqslant 10\) 时近似法计算的\(p\) 值可以给出较为满意的结果。另外，当 \(n>100\) 则建议不再进行连续性校正，即把校正部分的 \(-\frac{1}{2}\) 或者 \(-\frac{1}{2n}\) 去掉。

19.3.2 情况1：对均值进行假设检验 (方差已知)

假设从已知方差\((\sigma^2)\) 的人群中随机抽取样本进行血糖值测量\((Y_n)\)，该样本测量的人群的平均血糖值为$={Y} \(，假设我们要比较该人群的血糖值和某个理想血糖值\)_0$，进行假设检验：

\[\text{H}_0: \mu=\mu_0 \text{ v.s. H}_1: \mu\neq\mu_0\]

根据中心极限定理，当 \(n\) 足够大，样本均值 \(\bar{Y}\) 的分布接近正态分布，且均值 \(\mu\)，方差 \(\frac{\sigma^2}{n}\)。所以可以计算 \(Z\) 值：

\[ Z = \frac{\bar{Y}-E(\bar{Y})}{\sqrt{\text{Var}\bar{Y}}} = \frac{\bar{Y}-\mu_0}{ \sqrt{\sigma^2/n}} \]

进而计算其 \(p\) 值：

\[ \begin{aligned} p &= \text{Prob}(\bar{Y}\leqslant\bar{y}|\mu=\mu_0) \\ &= \text{Prob}(Z<\frac{\bar{y}-\mu_0}{\sqrt{\sigma^2/n}}) \\ &= \Phi(\frac{\bar{y}-\mu_0}{\sqrt{\sigma^2/n}}) \\ \text{Where } & \Phi \text{ is the distribution function for a } N(0,1) \text{distribution} \end{aligned} \]

所以计算了上面的单侧 \(p\) 值以后别忘了乘以 \(2\) 以获得双侧 \(p\) 值：

\[ \text{Two-sided } p \text{ value } = 2\times[1-\Phi(\frac{\bar{y}-\mu_0}{\sqrt{\sigma^2/n}})] \]

19.3.3 情况2：对均值进行假设检验 (方差未知)

如果方差未知，我们仍要比较一个样本均值和一个数值的话，零假设和替代假设依然不变：

\[\text{H}_0: \mu=\mu_0 \text{ v.s. H}_1: \mu\neq\mu_0\]

但是此时计算的统计量的分母，总体方差的地方使用了样本方差\(\frac{\hat\sigma^2}{n}\) 替代时，该统计量不再服从标准正态分布，而服从自由度为\(n-1\) 的\(t\) 分布。 \(t\) 分布看上去和标准正态分布很像，但是其分布的双侧尾部“较厚”，峰度大于 3：

\[ T = \frac{\bar{Y}-\mu_0}{\sqrt{\hat\sigma^2/n}} \sim t_{n-1} \]

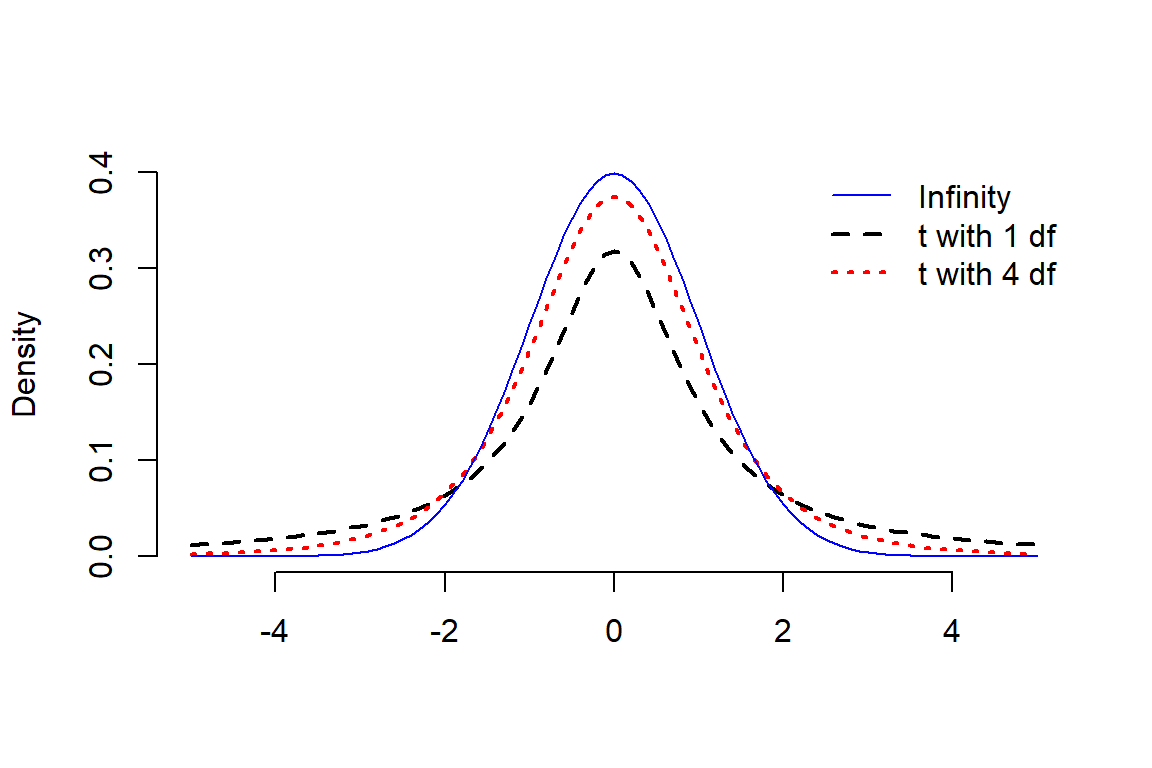
Student t distributions with 1, 4 and infinity degrees of freedom compared with a standard normal distribution

图 19.2: Student t distributions with 1, 4 and infinity degrees of freedom compared with a standard normal distribution

19.4 情况3：对配对实验数据的均值差进行假设检验

配对 t 检验 (the paired t-test)可以用于实验前后数据的比较，或者是某两个对象两两配对时的均值比较。这样的实验数据我们就可以去配对数据的差值，然后利用单样本 t 检验比较这个配对数据的差是否等于零。

计算获得了卡方值之后和自由度为 1 的卡方分布相比较获得双侧 \(p\) 值。

优化版本 用连续性校正法：

\[ \begin{aligned} \chi^2 &= \sum_i\sum_i(\frac{(|O_{ij}-E_{ij}| - 0.5)^2}{E_{ij}}) \\ \text{Where } &E_{ij} = \frac{O_{i\cdot}\times O_{\cdot j}}{O_{\cdot\cdot}} \end{aligned} \tag{19.3} \]

19.4.1 确切检验法

如果 \(2\times2\) 表格中的四个数字的 期待值 均大于 5，那么用上面的卡方检验没有问题，如果期待值都很小，就建议要使用精确检验法 (Fisher’s “exact” test)。 确切检验法的思想理论是超几何分布(Section 5.2)，在四个表格边缘合计固定不变的条件下，利用下面公式(19.4) 直接计算表内四个格子数据的各种组合的概率，然后计算单侧或者双侧累计概率，与显著性水平\(\alpha\) 比较。

\[ \begin{aligned} P_{O_{00}} & = \text{Prob}(O_{00},O_{01},O_{10},O_{11}|O_{0\cdot},O_{1\cdot},O_ {\cdot0},O_{\cdot1}) \\ & = \frac{O_{0\cdot}!O_{1\cdot}!O_{\cdot0}!O_{\cdot1}!}{O_{\cdot\cdot}!O_{00}!O_{01} !O_{10}!O_{11}!} \end{aligned} \tag{19.4} \]

在 R 里可以用 fisher.test 对四格表内容进行确切检验。

x3 <- matrix(c(7,5,3,8), ncol = 2, byrow = TRUE)
addmargins(x3)
##           Sum
##      7  5  12
##      3  8  11
## Sum 10 13  23
fisher.test(x3)
## 
##  Fisher's Exact Test for Count Data
## 
## data:  x3
## p-value = 0.2138
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
##   0.4941552 31.9433479
## sample estimates:
## odds ratio 
##   3.512801

19.5 多分类 (无排序) 的情况 \(M\times N\) 表格

卡方检验可以推广到两个多分类变量之间的相关分析。

\[ \begin{aligned} & \chi^2 = \sum_i\sum_j(\frac{(O_{ij}-E_{ij})^2}{E_{ij}}) \\ & \text{Where } E_{ij} = \frac{O_{i\cdot}O_{\cdot j}}{O_{\cdot\cdot}} \\ & \text{Under H}_0: \chi^2 \sim \chi^2_{(m-1)\times(n-1)} \end{aligned} \]

Observed data in a \(M\times N\) contingency table
\(Y = 1\) \(Y = 2\) \(\cdots\) \(Y = n\) Total
\(X = 1\) \(O_{11}\) \(O_{12}\) \(\cdots\) \(O_{1n}\) \(O_{1\cdot}\)
\(X = 2\) \(O_{21}\) \(O_{22}\) \(\cdots\) \(O_{2n}\) \(O_{2\cdot}\)
\(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\)
\(X = m\) \(O_{m1}\) \(O_{m2}\) \(\cdots\) \(O_{mn}\) \(O_{m\cdot}\)
Total \(O_{\cdot 1}\) \(O_{\cdot 2}\) \(\cdots\) \(O_{\cdot n}\) \(O_{\cdot\cdot}\)

Reference

Armitage, Peter, Geoffrey Berry, and John Nigel Scott Matthews. 2008. Statistical Methods in Medical Research. John Wiley & Sons.