第 17 章 探索数据和简单描述
17.1 数据分析的流程
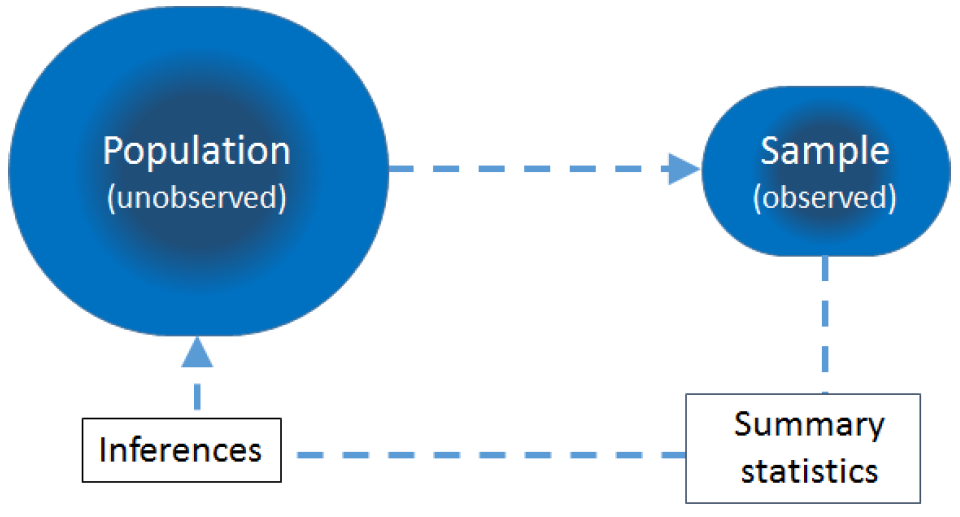
图 17.1: Population, sample and statistical inference
统计推断的目的,是通过从人群中取样本,经过对样本特征的 (描述) 统计分析 (summary statistic),去推断人群的相应特征。
所以,无论什么数据,到手以后我们一定要做的第一件事情,就是对其进行总结和描述,其过程又要尽可能地简单明了。
在绝大多数的科学研究中数据分析都很重要,然而现实是,它多数情况下只出现在研究的第三部分:
- 研究设计
- 实施研究,收集数据
- 数据分析
- 结果报告
17.1.1 研究设计和实施
正确的统计推断需要获得具有代表性可以值得分析的数据,这必须建立在实验研究设计良好,实施过程缜密的基础上。设计糟糕,执行效率低下或者漏洞百出的实验,给出的实验数据必然是不可靠的,分析它也没有意义。但是,不是说设计和实施阶段就不需要统计学家的参与了。相反地,统计学家必须在研究实施过程中尽可能早的阶段 (实验设计) 参与进来。因为理解了实验的目的,统计学家才能真正决定这个实验要收集怎样的数据,多大的样本量,实施怎样的分析方法。这些决定,注定了一项实验研究的成败。
17.1.2 数据分析
然而现实很残酷,多数情况下实验设计阶段好像没有统计学家什么事,等到了数据分析阶段,某些人才拍脑袋想让统计学家来拯救他们收集的垃圾数据。通常都太晚了 (too late!)。
假设理想状态下,我们收集到了想要分析的数据,可是接下来的工作流程的第一步,又常常被太多人忽略。许多 “科学家” 兴奋地把数据输入软件,立刻就开始着手建立数学模型,进行假设检验,却对数据的特征一无所知!要知道,建立怎样的模型,做怎样的推断,选用什么样的分析手段,都必须建立在你对数据内容完全熟悉的前提下,才能正确地实施。
数据分析第一步:数据清理, data cleaning。
这一步的目的很简单,把收集来的粗糙的,充满了缺失值和数据类型注解等等无法直接分析的数据,整理打扮成可以建模的数据库。这个过程中,你可能需要对某些变量进行分类,可能两三个实验的结果需要被合并协调,可能在这个过程中你会发现数据录入出现了一些错误导致数据库里有一些异常值,甚至是重复录入。所以,各位小伙伴当你拿到一个数据准备分析的第一步,你必须要先了解你的数据。常用的手段包括简单作图,对感兴趣的变量做概括分析 (summary your data!)。除此之外,由于没有人能保证实验中能收集到所有对象的完整数据,我们还需要分析缺失数据的特征,思考他们为什么会变成缺失数据。
17.2 数据类型
不同类型的数据,使用的初步描述手段各不相同。因此区分定性数据和定量数据,连续型数据,离散型数据,分类型数据显得十分必要。
- 连续型变量,continuous data
连续型数据多来自实验中对某些特征的测量,例如身高,体重等,它们本质上是一组连续型的数据。现实生活中接触到的许多数据也都是连续型的,例如:时间,距离,骨骼密度,药物浓度等等。所谓连续型变量是由于它理论上可以取某段数值区间内的任何值。当然我们还会被测量尺度的精确度所局限。 - 离散型变量,discrete data
许多数据,是通过计数来收集的。离散型变量的本质上也是属于数值型数据 (numeric),特征是这种数值型数据总是取正整数或者零。例如,医院中发生感染的次数,一个家庭中兄弟姐妹的人数,术后患者存活天数等等。 - 分类型变量,categorical data
分类型变量的数据,其每一个观察值都归类于一种类别 (或者属性)。分类型数据和离散型数据最大的不同是,它从本质上说就不属于数值型数据。例如,头发的颜色 (红色,黄色,黑色),职业类型 (装修工人,教师,总统)。尽管分类型数据本质上不是数值,分析过程中我们常常会给它们赋予一定的数值以便于计算。- 二分类型数据,binary:十分常见,例如,生存/死亡,有效/无效,成功/失败;
- 名义型数据,nominal:数据本身没有高低顺序之分,例如,种族,血型等;
- 排序型数据,ordinal:每个分类是包函了顺序含义的数据,例如,回答某些问卷问题时用的“十分同意,同意,不同意,十分不同意”,某些癌症使用的分级诊断“一级,二级,三级,终级”,对一些结果的评价时使用的“优,良,中,差”。
其实,对于连续型变量我们还常常会将它们转化成分类型变量,使用一些特定的或者事先定义好的阈值 (cutoff values) 把连续型数据分组,分级,分层等等。最常见的例子就是体重指数(BMI),它本身是一个连续型的变量,但是又可以根据定义好的阈值把它分类成低体重(\(< 18.5 \; kg/m^2\)),正常体重(\(18.5 - 24.9 \; kg/m^2\)),超重(\(25-29.9 \; kg/m^2\)),肥胖(\(\geqslant 30 \; kg/m^2\))。另一个例子是血红蛋白(haemoglobin, \(g/l\)),它本身是一个连续型变量,但是我们利用它的阈值(女性,\(<120 \; g/l\);男性,\(< 130 \; g /l\)),作为诊断是否患有贫血症的依据。
把连续型变量进行分类处理的代价是信息的丢失。如果一个人的体重指数是 \(25\),他/她的数据被和体重指数为 \(29.9\) 的人当作相同数值来对待是否合理是我们需要考虑的问题。而且许多情况下阈值的定义并不能达成共识,即使达成共识的阈值又是十分人为且恣意的,它可能导致一些相关关系被“强化”,或者反过来被“弱化”。所以,如果要对连续型数值进行分组,现在的要求是,在实验设计阶段就必须明确分组的阈值之定义,而不能在看到数据以后进行人为地划分。 更加不推荐的是直接使用四分位或者五分位来对数据分组。
17.3 如何总结并展示数据
光观察原始数据很难真正明白数据的分布特征和形式,所以使用表格,或者用散点图,柱状图等形式来描述数据就成为了常用的手段。前一节所描述的数据类型,决定了一组数据该如何被描述。
17.3.1 离散型分类型数据的描述 - 频数分布表 frequency table
下面的表格就是使用频数分布表来描述 cars 这个数据包中不同车速 (mph) 的分布。汽车车速本身应该是一个连续型变量,但是这是1920年的数据当时的记录只精确到整数,因此人为地造成了一组离散型变量的情况。下面的第二个表格使用的是 ggplot2 里自带的钻石数据。其中 cut 是对于钻石切割水平的评价,所以是一个带有排序性质的分组型变量。
## cars$speed :
## Frequency Percent Cum. percent
## 4 2 4 4
## 7 2 4 8
## 8 1 2 10
## 9 1 2 12
## 10 3 6 18
## 11 2 4 22
## 12 4 8 30
## 13 4 8 38
## 14 4 8 46
## 15 3 6 52
## 16 2 4 56
## 17 3 6 62
## 18 4 8 70
## 19 3 6 76
## 20 5 10 86
## 22 1 2 88
## 23 1 2 90
## 24 4 8 98
## 25 1 2 100
## Total 50 100 100## diamonds$cut :
## Frequency Percent Cum. percent
## Fair 1610 3.0 3.0
## Good 4906 9.1 12.1
## Very Good 12082 22.4 34.5
## Premium 13791 25.6 60.0
## Ideal 21551 40.0 100.0
## Total 53940 100.0 100.0离散型变量和分类型变量的描述还可以使用柱状图的形式来展示如下:
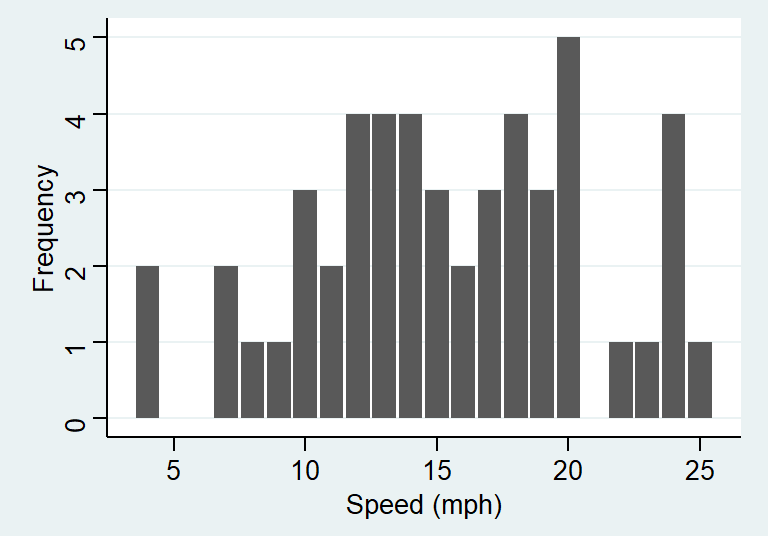
图 17.2: Bar chart displaying the speed of cars
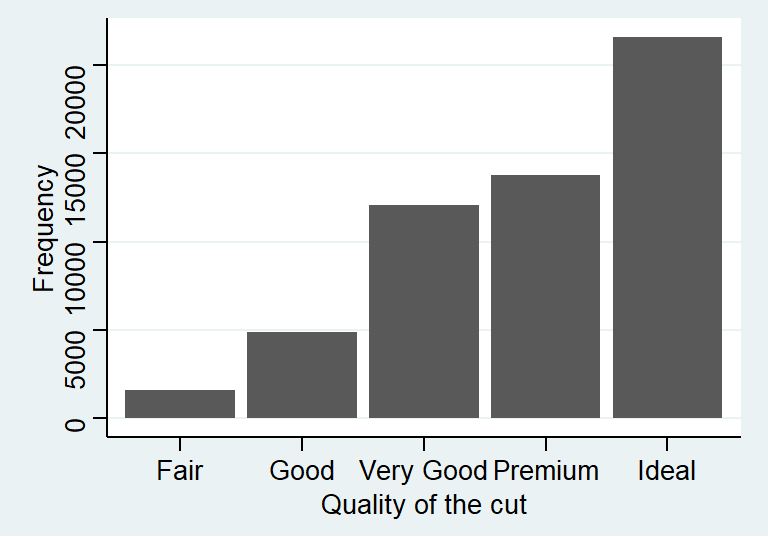
图 17.3: Bar chart displaying distribution of evaluation of diamonds cut
上面这两图的 y 轴都用的是频率,当然还可以使用百分比。不同组间分类型变量的分布比较的话更常使用百分比作为 y 轴。如下面的表格及百分比条形图所示。
diamonds$clarity2g <- "Good"
diamonds$clarity2g[(diamonds$clarity=="I1")|
(diamonds$clarity=="SI2")|
(diamonds$clarity=="SI1")|
(diamonds$clarity=="VS2")] <- "Poor"
tab <- stat.table(index=list(Cut=cut,Clarity=clarity2g),
contents=list(count(),percent(cut)), data=diamonds, margins=T)
print(tab, digits = 2)## ---------------------------------------
## ----------Clarity-----------
## Cut Good Poor Total
## ---------------------------------------
## Fair 265.00 1345.00 1610.00
## 1.42 3.81 2.98
##
## Good 1191.00 3715.00 4906.00
## 6.38 10.54 9.10
##
## Very Good 4067.00 8015.00 12082.00
## 21.77 22.73 22.40
##
## Premium 3705.00 10086.00 13791.00
## 19.83 28.61 25.57
##
## Ideal 9454.00 12097.00 21551.00
## 50.60 34.31 39.95
##
##
## Total 18682.00 35258.00 53940.00
## 100.00 100.00 100.00
## ---------------------------------------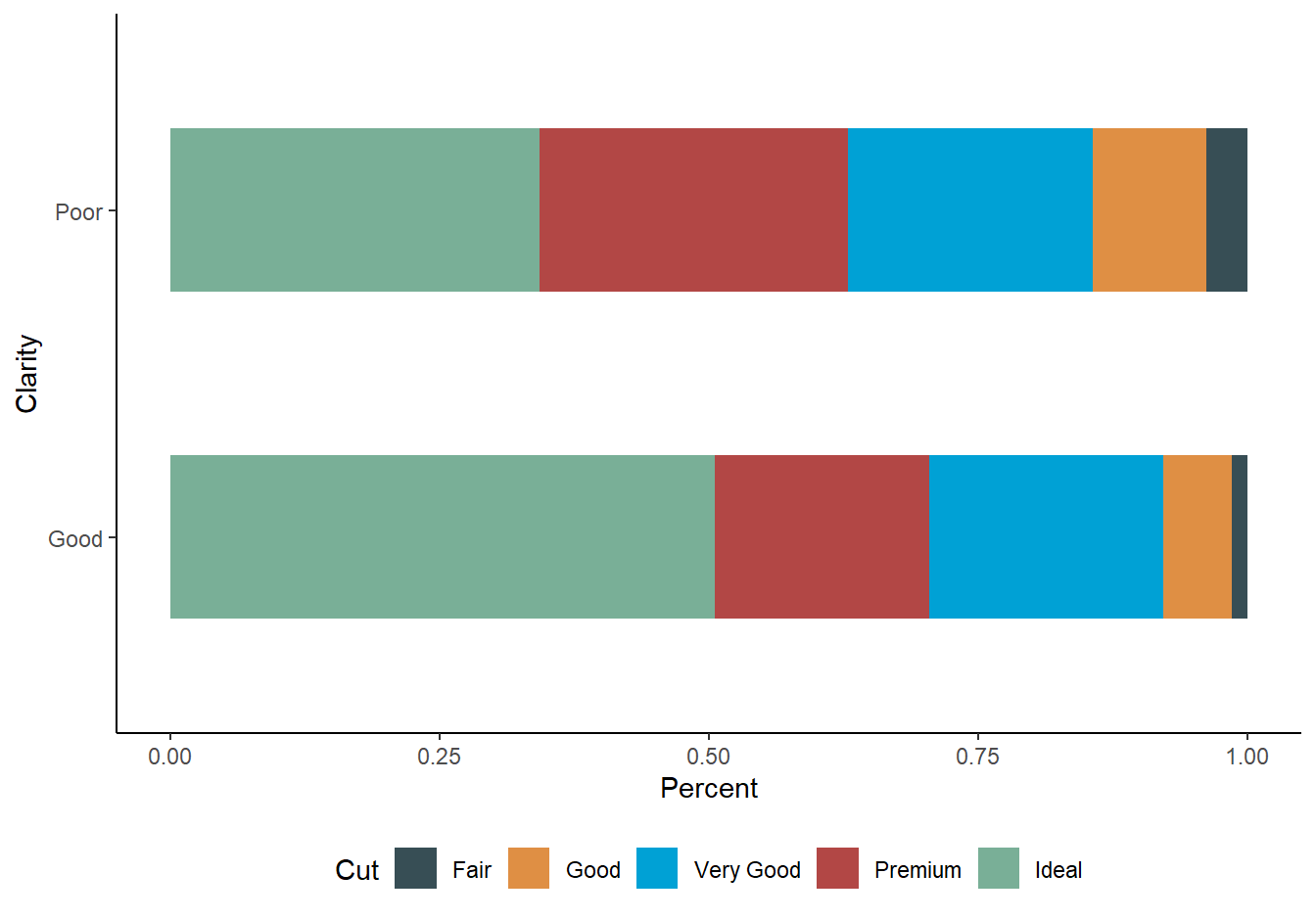
图 17.4: Bar chart displaying distribution of evaluation of diamonds cut by clarity
17.3.2 连续型变量
连续型变量如果做频数分布表一般提供的信息量就较小。常用来描述连续型变量的手段是柱状图,histogram,和箱形图,boxplot。柱状图应该不必过多解释。箱形图,展示的是连续型变量的中位数,四分位,范围值,以及异常值。一个典型的箱形图,中间的方形区域包括了该数据的四分位距,interquartile range (即中间 50% 的数据, IQR)。
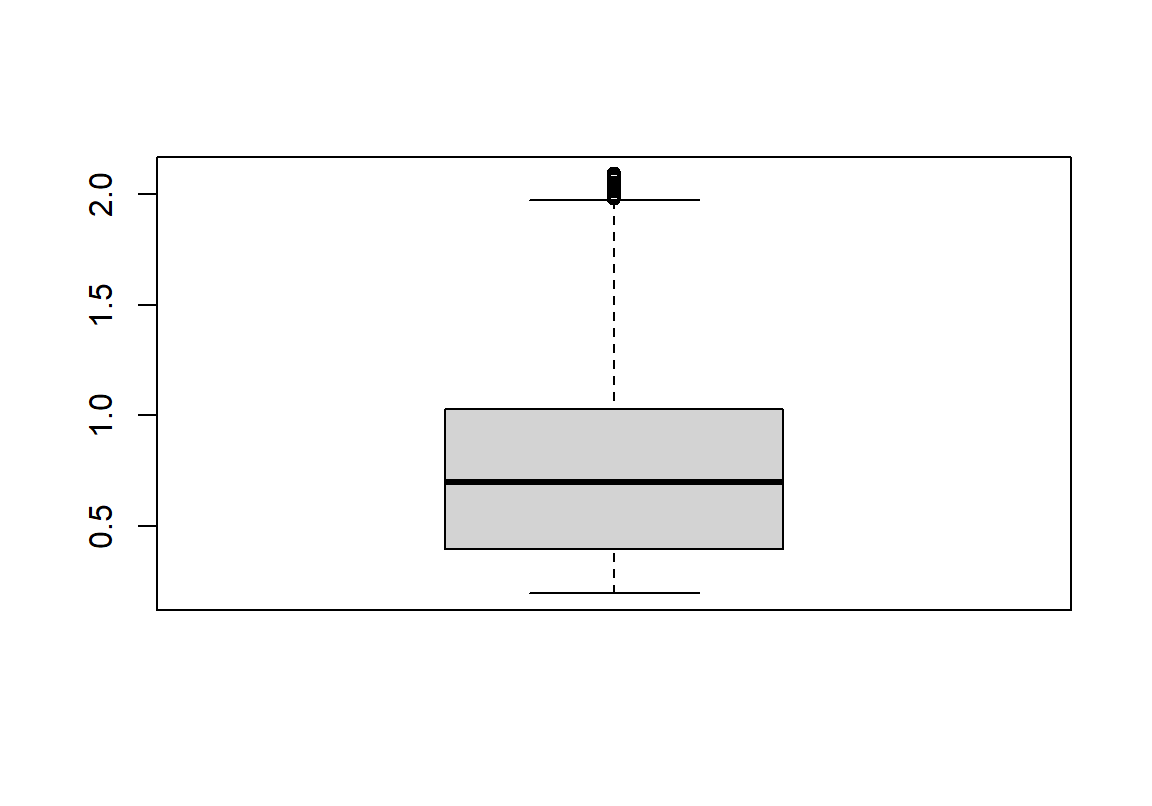
图 17.5: Boxplot of the diamond carat data
R作出的箱形图如17.5 所示,箱子以上的横线,意为最高值为75%分位值加上1.5倍的IQR;箱子以下横线,意为最低值为25%分位值减去1.5倍的IQR。其他的观察值如果不在这个上下限范围之内的,会用黑点标记出来。这些值被认为是异常值 (outliers)。
17.4 数据总结方案:位置,分散,偏度,和峰度
17.4.1 位置
描述一组连续型变量的位置,location,此处的位置指的是数据分布的中心位置,常用的数值是众数 (mode),中位数 (median),均值 (mean)。
- 众数 mode,的定义是,一组数据中出现最多次的数值大小;
- 中位数median,的定义是,一组数据中从小到大/或者从大到小排序后50%位置的数值大小,如果观察值有偶数个,中位数的定义是中间两个数值的平均值大小;
- 算术平均值arithmetic mean 的大小受异常值影响较大,通常简略为均值,其定义可以用下面的表达式:\[\bar{X}=\frac{1}{n}\ sum_{i=1}^n X_i\]
- 几何平均值geometrix mean,常用在正偏态分布数据(positively skewed data),其定义为: \[\sqrt[n]{\prod_{i=1}^n X_i}=exp[\frac{1 }{n}\sum_{i=1}^n log_e(X_i)]\]
- 调和平均值harmonic mean,是所有观察值的倒数和的倒数,定义为:\[\frac{1}{\frac{1}{n}\sum_{i=1}^n\frac{1} {X_i}}\]
17.4.2 分散
数据的分散程度,dispersion,也就是数据的波动大小 variation。同样均值的数据,他们的分散可能差别很大:
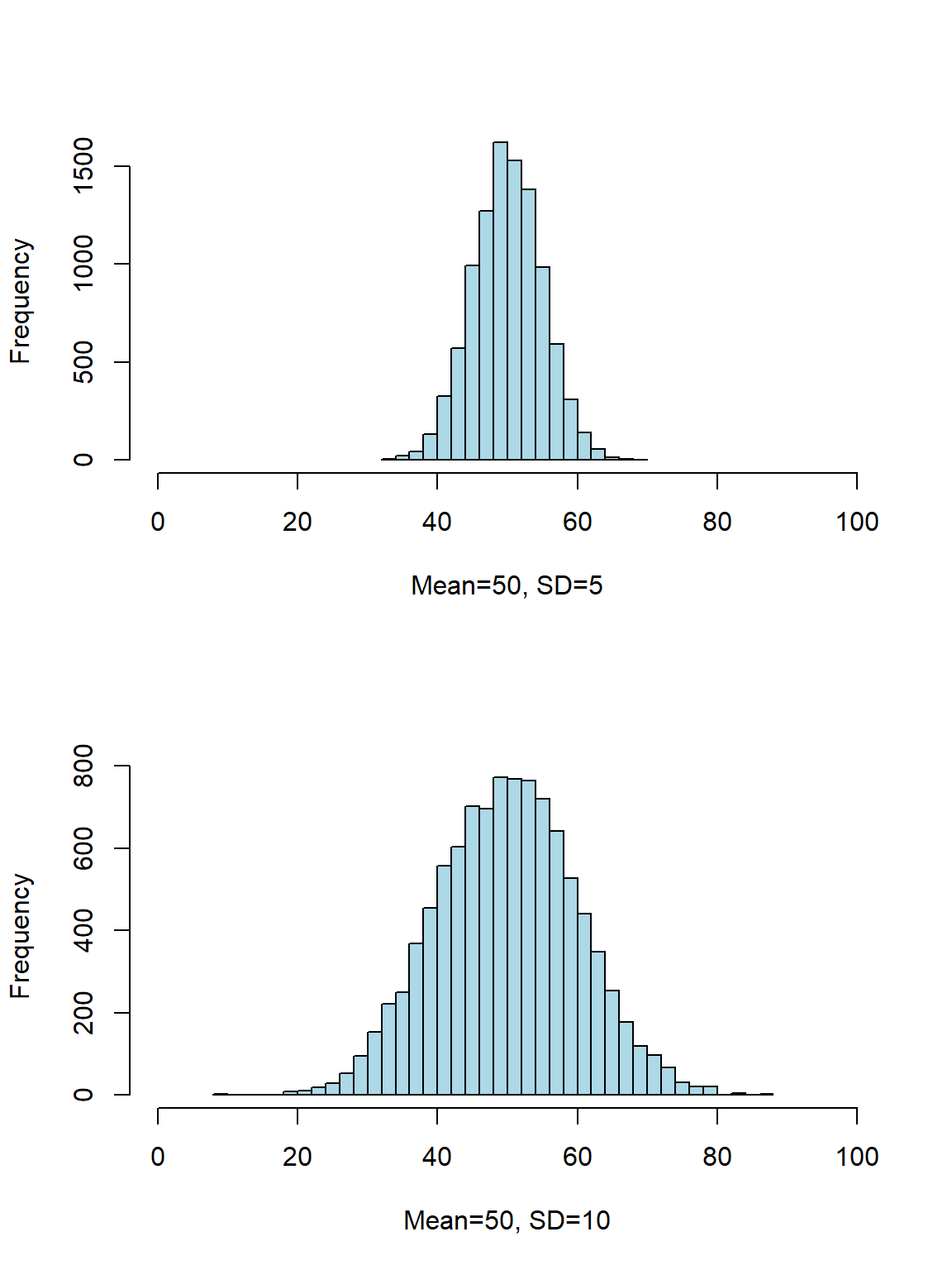
图 17.6: Distributions with similar central location but different dispersion
分散程度的描述方法花样不少,我们这里先考虑范围 (range),四分位差 (interquartile range),方差 (variance),标准差 (standard deviation)。
17.4.2.2 四分位差
定义:四分位差 (interquartile range, IQR)是包含了数据中间 50% 数值的范围。即,75%分位数-25%分位数的差值。
当观察值数量为奇数个时,计算方法为:去掉中位数,计算大于中位数和小于两个部分数值的中位数,求其差,例如:\(5,10,12,14,16 ,19,22\) 这组数字,25%分位数为10,75%分位数为19,所以IQR等于9。
当观察值数量为偶数个时,计算方法为:计算较小的50%数值的中位数,和较大50%数值的中位数,求其差,例如:\(5,10,12,14 ,16,19,22,38\) 这组数字,上下两半部分的中位数分别是\(Q_L=\frac{10+12}{2}=11;\;Q_U=\frac{19+22} {2}=20.5\),所以,其IQR等于9.5.
在表格,论文中需要同时报告25%,75%分位数两个数值,例:[11,20.5]。
17.4.2.3 方差和标准差
先定义每一个观察值和均值之间的差为 \(D_i = X_i - \bar{X}\)。
根据定义,\(\frac{1}{n}\sum_{i=1}^n D_i=0\)。
样本方差 Variance 被定义为 \(\frac{1}{n-1}\sum_{i=1}^n D_i^2\)。
样本方差的平方根,被定义为标准差 standard deviation,\(\text{SD}=\sqrt{\frac{1}{n-1}\sum_{i=1}^n D_i^2}\)
更常见的表达式为:
\[ \begin{aligned} \text{Var} &= \frac{1}{n-1}\sum_{i=1}^n (X_i-\bar{X})^2 \\ &= \frac{1}{n-1}[(\sum_{i=1}^nX_i^2)-n\bar{X}^2] \end{aligned} \]
此处分母为 \(n-1\) 而不是 \(n\) 的原因,需要参考推断部分的解释 (Section 10.3)。
- 方差标准差受异常值影响较大。例如,下面的数据:
\[ 5, 9, 12, 14, 14, 15, 16, 19, 22\;\;\; \text{Var}=25.5\\ 5, 9, 12, 14, 14, 15, 16, 19, 58\;\; \text{Var}=241.5 \]
17.4.3 偏度 skewness
使用柱状图来描述数据时,如果柱状图左右基本对称 (中位数和均值基本一致),偏度为零,正态分布数据都是左右对称的。如果柱状图右侧的尾巴较长,偏度为正;如果左侧的尾巴较长,偏度为负。偏度计算公式为:
\[ \frac{\frac{1}{n}\sum_{i=1}^n D_i^3}{(\frac{1}{n}\sum_{i=1}^n D_i^2)^{\ frac{3}{2}}} \]
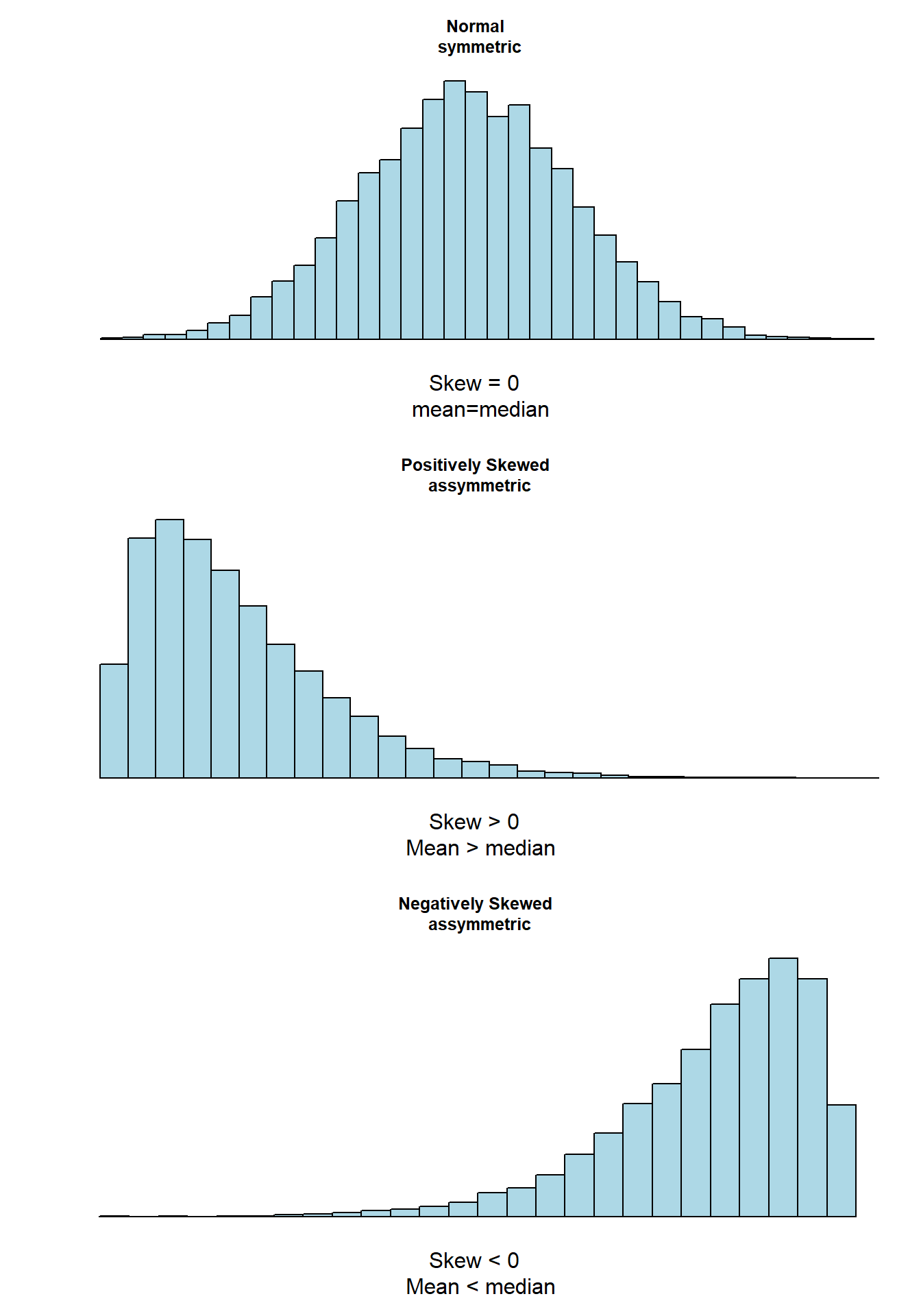
图 17.7: Relationship between skew and measures of location
17.4.4 峰度 kurtosis
峰度是描述数据分布的最后一个指标。峰度衡量的是一组数据分布的尾部的厚度。一个正态分布数据,大约 5% 的数据分布在左右两边的尾部 (2.5% 低于 \(\mu-2\sigma\),2.5% 高于 \(\mu +2\sigma\))。峰度测量的是一组数据尾部数据的分布和正态分布两侧尾部数据之间的差距。
峰度的计算公式为: \[ \frac{\frac{1}{n}\sum_{i=1}^nD_i^4}{(\frac{1}{n}\sum_{i=1}^nD_i^2)^2} \] 一个正态分布数据,峰度值为 3。当左右两段的数值占比低于正态分布预期时,峰度值小于 3。反之,峰度大于 3。尾部较厚 (峰度较大) 的典型分布之一是 \(t\) 分布 (图 17.8)
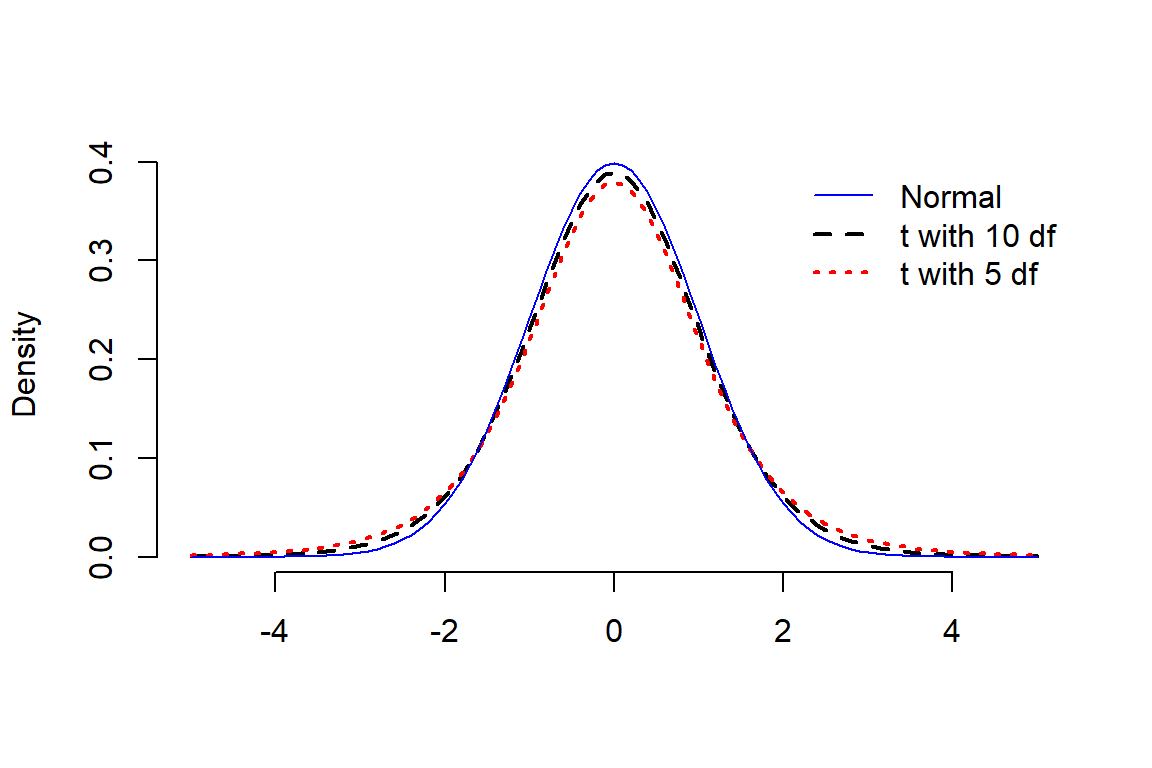
图 17.8: t distributions with 5 and 10 degrees of freedom compared with a standard normal distribution