第 13 章 对数似然比

对数似然比的想法来自于将对数似然方程图形的 \(y\) 轴重新调节 (rescale) 使之最大值为零。这可以通过计算该分布方程的对数似然比 (log-likelihood ratio) 来获得：

\[llr(\theta)=\ell(\theta|data)-\ell(\hat{\theta}|data)\]

由于\(\ell(\theta)\) 的最大值在\(\hat{\theta}\) 时， 所以，\(llr(\theta)\) 就是个当\(\theta=\hat{\theta}\) 时取最大值，且最大值为零的方程。很容易理解我们叫这个方程为对数似然比，因为这个方程就是将似然比\(LR(\theta)=\frac{L(\theta)}{L(\hat{\theta})}\) 取对数而已。

之前(Section 12)我们也确证了，不包含我们感兴趣的参数的方程部分可以忽略掉。还是用上一节 10人中4人患病的例子：

\[L(\pi|X=4)=\binom{10}{4}\pi^4(1-\pi)^{10-4}\\ \Rightarrow \ell(\pi)=\text{log}[\pi^4(1-\pi)^{10-4}]\\ \Rightarrow llr(\pi)=\ell(\pi)-\ell(\hat{\pi})=\text{log}\frac{\pi^4(1-\pi)^{10-4}}{0.4^4(1-0.4)^{10-4}}\]

其实由上也可以看出 \(llr(\theta)\) 只是将对应的似然方程的 \(y\) 轴重新调节了一下而已。形状是没有改变的：

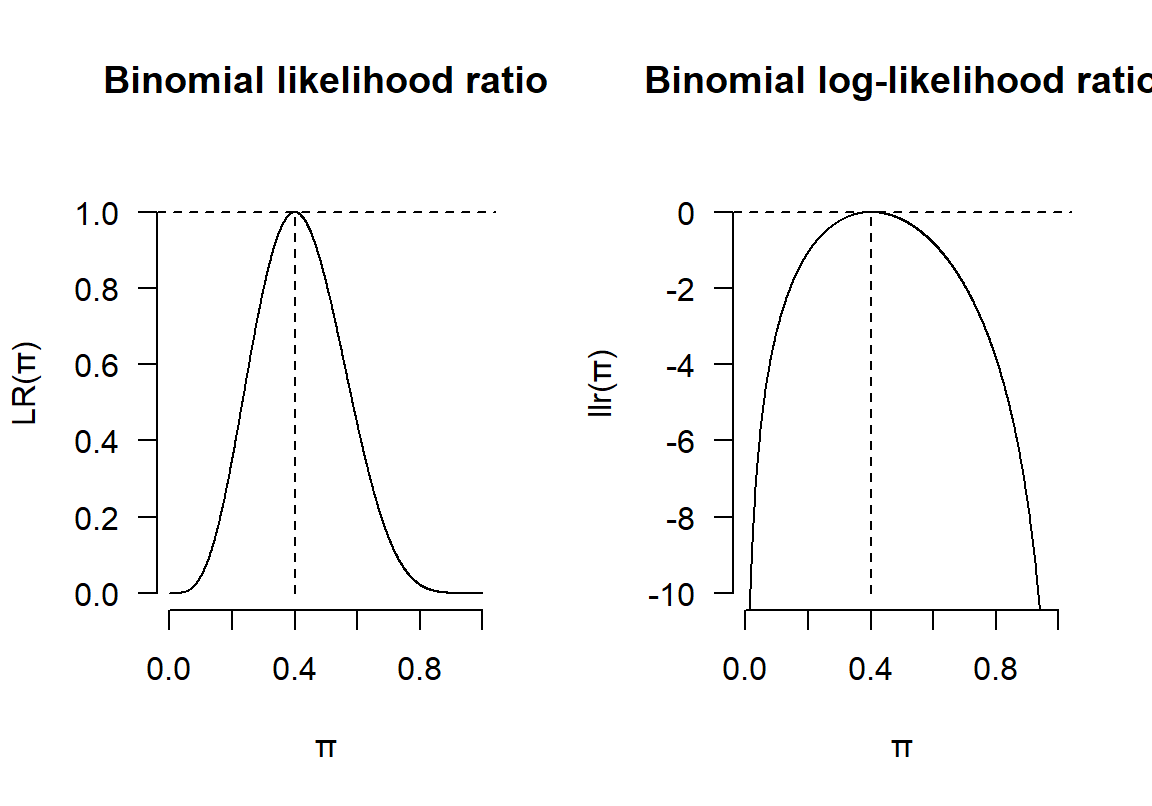
Binomial likelihood ratio and log-likelihood ratio

图 13.1: Binomial likelihood ratio and log-likelihood ratio

13.1 正态分布数据的极大似然和对数似然比

假设单个样本 \(y\) 是来自一组服从正态分布数据的观察值：\(Y\sim N(\mu, \tau^2)\)

那么有：

\[ \begin{aligned} f(y|\mu) &= \frac{1}{\sqrt{2\pi\tau^2}}e^{(-\frac{1}{2}(\frac{y-\mu}{\tau})^2)} \\ \Rightarrow L(\mu|y) &=\frac{1}{\sqrt{2\pi\tau^2}}e^{(-\frac{1}{2}(\frac{y-\mu}{\tau})^2)} \\ \Rightarrow \ell(\mu)&=\text{log}(\frac{1}{\sqrt{2\pi\tau^2}})-\frac{1}{2}(\frac{y-\mu}{\tau})^2\\ omitting&\;terms\;not\;in\;\mu \\ &= -\frac{1}{2}(\frac{y-\mu}{\tau})^2 \\ \Rightarrow \ell^\prime(\mu) &= 2\cdot[-\frac{1}{2}(\frac{y-\mu}{\tau})\cdot\frac{-1}{\tau}] \\ &=\frac{y-\mu}{\tau^2} \\ let \; \ell^\prime(\mu) &= 0 \\ \Rightarrow \frac{y-\mu}{\tau^2} &= 0 \Rightarrow \hat{\mu} = y\\ \because \ell^{\prime\prime}(\mu) &= \frac{-1}{\tau^2} < 0 \\ \therefore \hat{\mu} &= y \Rightarrow \ell(\hat{\mu}=y)_{max}=0 \\ llr(\mu)&=\ell(\mu)-\ell(\hat{\mu})=\ell(\mu)\\ &=-\frac{1}{2}(\frac{y-\mu}{\tau})^2 \end{aligned} \]

13.2 \(n\) 个独立正态分布样本的对数似然比

假设一组观察值来自正态分布 \(X_1,\cdots,X_n\stackrel{i.i.d}{\sim}N(\mu,\sigma^2)\)，先假设 \(\sigma^2\) 已知。将观察数据 \(x_1,\cdots, x_n\) 标记为 \(\underline{x}\)。那么：

\[ \begin{aligned} L(\mu|\underline{x}) &=\prod_{i=1}^nf(x_i|\mu)\\ \Rightarrow \ell(\mu|\underline{x}) &=\sum_{i=1}^n\text{log}f(x_i|\mu)\\ &=\sum_{i=1}^n[-\frac{1}{2}(\frac{x_i-\mu}{\sigma})^2]\\ &=-\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2\\ &=-\frac{1}{2\sigma^2}[\sum_{i=1}^n(x_i-\bar{x})^2+\sum_{i=1}^n(\bar{x}-\mu)^2]\\ omitting&\;terms\;not\;in\;\mu \\ &=-\frac{1}{2\sigma^2}\sum_{i=1}^n(\bar{x}-\mu)^2\\ &=-\frac{n}{2\sigma^2}(\bar{x}-\mu)^2 \\ &=-\frac{1}{2}(\frac{\bar{x}-\mu}{\sigma/\sqrt{n}})^2\\ \because \ell(\hat{\mu}) &= 0 \\ \therefore llr(\mu) &= \ell(\mu)-\ell(\hat{\mu}) = \ell(\mu) \end{aligned} \]

13.3 \(n\) 个独立正态分布样本的对数似然比的分布

假设我们用 \(\mu_0\) 表示总体均数这一参数的值。要注意的是，每当样本被重新取样，似然，对数似然方程，对数似然比都随着观察值而变 (即有自己的分布)。

考虑一个服从正态分布的单样本 \(Y\): \(Y\sim N(\mu_0,\tau^2)\)。那么它的对数似然比：

\[llr(\mu_0|Y)=\ell(\mu_0)-\ell(\hat{\mu})=-\frac{1}{2}(\frac{Y-\mu_0}{\tau})^2\] 根据卡方分布 ( Section 11 ) 的定义：

\[\because \frac{Y-\mu_0}{\tau}\sim N(0,1)\\ \Rightarrow (\frac{Y-\mu_0}{\tau})^2 \sim \mathcal{X}_1^2\\ \therefore -2llr(\mu_0|Y) \sim \mathcal{X}_1^2\]

所以，如果有一组服从正态分布的观察值：\(X_1,\cdots,X_n\stackrel{i.i.d}{\sim}N(\mu_0,\sigma^2)\)，且\(\sigma^2\) 已知的话：

\[-2llr(\mu_0|\bar{X})\sim \mathcal{X}_1^2\]

根据中心极限定理 ( Section 8 )，可以将上面的结论一般化：

如果 \(X_1,\cdots,X_n\stackrel{i.i.d}{\sim}f(x|\theta)\)。那么当重复多次从参数为\(\theta_0\) 的总体中取样时，那么统计量\(-2llr(\theta_0)\) 会渐进于自由度为\(1\) 的卡方分布： \[-2llr(\theta_0) =-2\{\ell(\theta_0)-\ell(\hat{\theta})\}\xrightarrow[n\rightarrow\infty]{}\;\sim \mathcal{X}_1^2\]

13.4 似然比置信区间

如果样本量 \(n\) 足够大 (通常应该大于 \(30\))，根据上面的定理：

\[-2llr(\theta_0)=-2\{\ell(\theta_0)-\ell(\hat{\theta})\}\sim \mathcal{X}_1^2\]

所以：

\[Prob(-2llr(\theta_0)\leqslant \mathcal{X}_{1,0.95}^2=3.84) = 0.95\\ \Rightarrow Prob(llr(\theta_0)\geqslant-3.84/2=-1.92) = 0.95\]

故似然比的 \(95\%\) 置信区间就是能够满足 \(llr(\theta)=-1.92\) 的两个 \(\theta\) 值。

13.4.1 以二项分布数据为例

继续用本文开头的例子：

\[llr(\pi)=\ell(\pi)-\ell(\hat{\pi})=\text{log}\frac{\pi^4(1-\pi)^{10-4}}{0.4^4(1-0.4)^{10-4}}\]

如果令 \(llr(\pi)=-1.92\) 在代数上可能较难获得答案。然而从图形上，如果我们在 \(y=-1.92\) 画一条横线，和该似然比方程曲线相交的两个点就是我们想要求的置信区间的上限和下限：

Log-likelihood ratio for binomial example, with 95% confidence intervals shown

图 13.2: Log-likelihood ratio for binomial example, with 95% confidence intervals shown

从上图中可以读出，\(95\%\) 对数似然比置信区间就是 \((0.15, 0.7)\)

13.4.2 以正态分布数据为例

本文前半部分证明过， \(X_1,\cdots,X_n\stackrel{i.i.d}{\sim}N(\mu,\sigma^2)\)，先假设 \(\sigma^2\) 已知。将观察数据 \(x_1,\cdots, x_n\) 标记为 \(\underline{x}\)。那么：

\[llr(\mu|\underline{x}) = \ell(\mu|\underline{x})-\ell(\hat{\mu}) = \ell(\mu|\underline{x}) \\ =-\frac{1}{2}(\frac{\bar{x}-\mu}{\sigma/\sqrt{n}})^2\]

很显然，这是一个关于 \(\mu\) 的二次方程，且最大值在 MLE \(\hat{\mu}=\bar{x}\) 时取值 \(0\)。所以可以通过对数似然比法求出均值的 \(95\%\) 置信区间公式：

\[-2\times[-\frac{1}{2}(\frac{\bar{x}-\mu}{\sigma/\sqrt{n}})^2]=3.84\\ \Rightarrow L=\bar{x}-\sqrt{3.84}\frac{\sigma}{\sqrt{n}} \\ U=\bar{x}+\sqrt{3.84}\frac{\sigma}{\sqrt{n}} \\ note: \;\sqrt{3.84}=1.96\]

注意到这和我们之前求的正态分布均值的置信区间公式 ( Section 10.1 ) 完全一致。