第 23 章 简单线性回归
23.1 一些背景和术语
思考下面这些问题:
- 脂肪摄入量增加,会导致体重增加吗?
- 儿童成年时的身高,可以用父母亲的身高来预测吗?
- 如果其他条件都没有变化,饮食习惯的改变,是否能影响血清胆固醇的水平?
上面的问题中,自变量 (预测变量),和因变量 (反应量) 分别是什么?
你可能还会碰到像下面这些称呼,他们都是一个意思:
- 因变量 Dependent variable = 反应量 response variable = 结果变量 outcome variable;
- 自变量 independent variable = 预测变量 predictor variable = 解释变量 explanatory variable = 共变量 covariate.
所有的非简单统计模型 (non-trivial statistical models) 都包括以下三个部分:
- 随机变量 random variables:
- 因变量永远都是随机变量;
- 预测变量不一定是随机变量;
- 在相对简单的模型中,我们讨论的因变量和预测变量几乎都来自于从人群中抽取观察样本收集来的数据。
- 人群参数 population parameters:
- 人群参数,是我们希望通过收集样本获得的数据来估计 (estimate) 的参数。
- 对不确定性的描述 representation of uncertainty:
- 不确定性,意为因变量的变动中,没有被预测变量解释的部分。
其他的术语问题:
- 单一因变量的统计模型:univariate model;
- 多个因变量的统计模型: multivariate model;
- 单一因变量,含有多个预测变量的统计模型:multivariable model;
- 在线性回归中,单一因变量,单一预测变量的统计模型:simple linear regression (简单线性回归);
- 在线性回归中,单一因变量,多个预测变量的统计模型:multiple linear regression (多重线性回归);
尽量避免将预测变量 (predictor variable) 写作自变量 (independent variable),因为 “independent” 有自己的统计学含义 (独立)。然而我们在线性回归中使用的预测变量,不一定都互相独立,所以容易让人混淆其意义。
23.2 简单线性回归模型
即:单一因变量,单一预测变量的统计模型。
23.2.1 数据 A
下面的散点图 23.1 展示的是一项横断面调查的结果,调查的是一些儿童的年龄 (月),和他们的体重 (千克) 之间的关系。
library(haven)
library(ggplot2)
library(ggthemes)
growgam1 <- read_dta("../Datas/growgam1.dta")
ggplot(growgam1, aes(x=age, y=wt)) + geom_point(shape=20) +
scale_x_continuous(breaks=seq(0, 38, 4),limits = c(0,36.5))+
scale_y_continuous(breaks = seq(0, 20, 5),limits = c(0,20.5)) +
theme_stata() +labs(x = "Age (Months)", y = "Weight (kg)")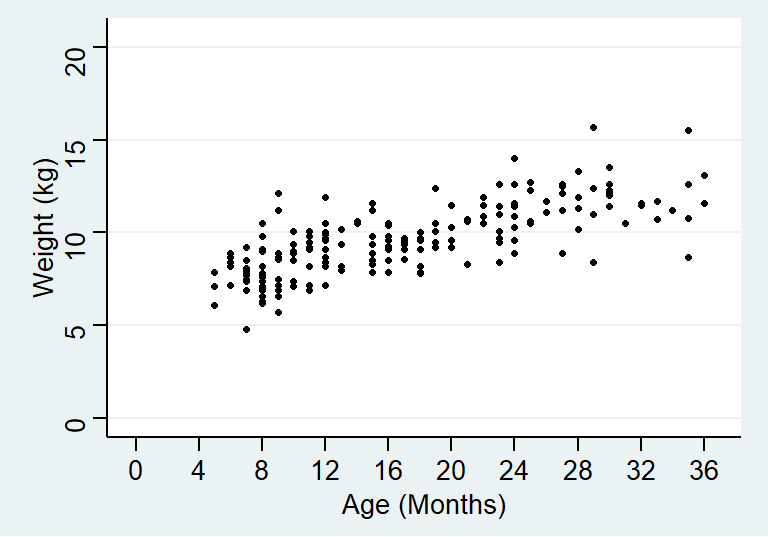
图 23.1: Age and weight of children in a cross-sectional survey
23.2.2 数据 B
表 23.1 罗列的是11名儿童能够自己独立行走时的年龄。这些儿童在刚出生时被随机分配到两个组中 (积极锻炼走路,和对照组)。如果你熟悉均数比较,这样的数据可以通过简单 \(t\) 检验来分析其均值的不同。但是实际上后面你会看到简单 \(t\) 检验和简单线性回归是同一回事。
| Active Exercise (n=6) | Eight Week Control (n=5) |
|---|---|
| 9.00 | 13.25 |
| 9.50 | 11.5 |
| 9.75 | 12 |
| 10.00 | 13.5 |
| 13.00 | 11.5 |
| 9.50 | – |
23.3 区分因变量和预测变量
在简单两样本 \(t\) 检验中,我们不区分那两个要比较的数据 \((X, Y)\)。所以 \(X\) 和 \(Y\) 的关系,同分析 \(Y\) 和 \(X\) 的关系是一样的。表 23.1 的例子中,视“直立行走的年龄”这一变量为因变量十分直观且自然。图 23.1 的例子中我们显然可以关心是否可以用儿童的年龄来推测他/她的体重。所以年龄被视为预测变量 \((X)\),体重被视为因变量或者叫结果变量 \((Y)\)。
23.3.1 均值 (期待值) 公式
图23.1 的例子中,当我们决定考察体重变化\((Y)\) 和年龄的关系\((X)\) 后,我们需要提出一个模型,来描述二者之间的关系。这个模型中,最重要的信息,是均值,或者叫期待值:
\[ E(Y|X=x), \text{ the expected value of } Y \text{ when } X \text{ takes the value } x \]
在简单线性回归模型中,我们认为这个均值方程是线性关系:
\[ E(Y|X=x) = \alpha +\beta x \]
所以这个线性关系中,有两个参数 (parameters) 是我们关心的 \(\alpha, \beta\)。
- \(\alpha\) 是截距 intecept。意为当 \(X\) 取 \(0\)时, \(Y\) 的期待值大小;
- \(\beta\) 是方程的斜率 slope。意为当 \(X\) 上升一个单位时,\(Y\) 上升的期待值大小。
需要强调的是,这样的线性模型,是我们提出,用来模拟真实数据时使用的。 你如果作死当然还可以提出更加复杂的模型。如下面图 23.2 显示的是线性回归直线, 而图 23.3 显示的是较为复杂的回归曲线。曲线方程可能更加拟合我们收集到的数据,然而这样的连续的斜率变化很可能仅仅只解释了这个样本量数据,而不能解释在人群中年龄和体重的关系。
library(haven)
library(ggplot2)
library(ggthemes)
growgam1 <- read_dta("../Datas/growgam1.dta")
ggplot(growgam1, aes(x=age, y=wt)) + geom_point(shape=20, colour="grey40") +
stat_smooth(method = lm, linewidth = 0.3) +
scale_x_continuous(breaks=seq(0, 38, 4),limits = c(0,36.5))+
scale_y_continuous(breaks = seq(0, 20, 5),limits = c(0,20.5)) +
theme_stata() +labs(x = "Age (Months)", y = "Weight (kg)")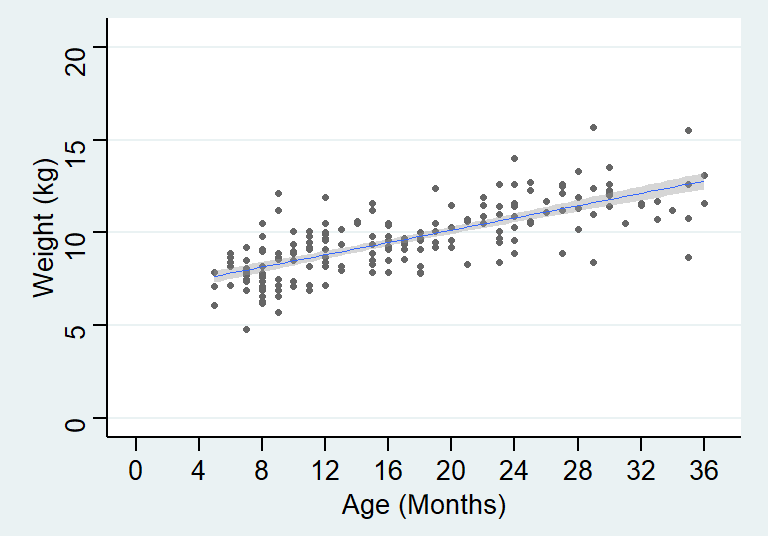
图 23.2: Linear mean function for age and weight of children in a cross-sectional survey
library(haven)
library(ggplot2)
library(ggthemes)
growgam1 <- read_dta("../Datas/growgam1.dta")
ggplot(growgam1, aes(x=age, y=wt)) + geom_point(shape=20, colour="grey40") +
stat_smooth(method = loess, se=T, linewidth = 0.3) +
scale_x_continuous(breaks=seq(0, 38, 4),limits = c(0,36.5))+
scale_y_continuous(breaks = seq(0, 20, 5),limits = c(0,20.5)) +
theme_stata() +labs(x = "Age (Months)", y = "Weight (kg)")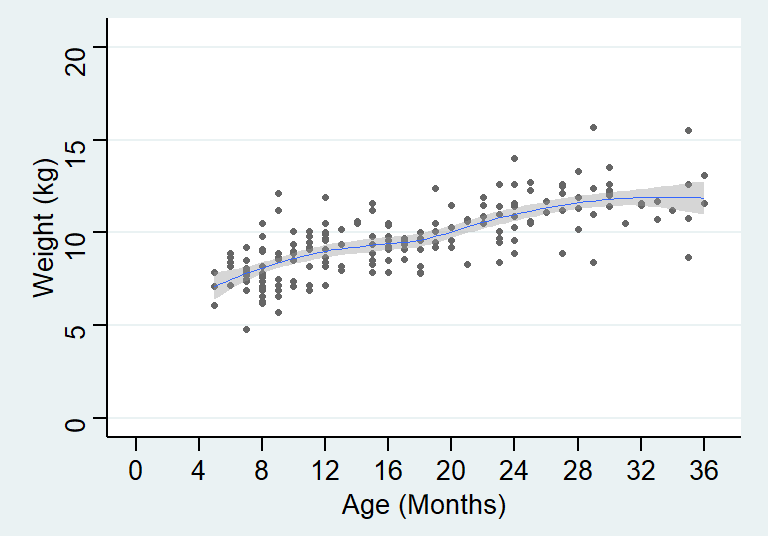
图 23.3: Non-linear mean function for age and weight of children in a cross-sectional survey
23.3.2 条件分布和方差
如果要完全明确一个统计模型,另一个重要的点在于,提出的模型能否准确描述因变量在预测变量的条件下的分布(conditional distribution) it is necessary to describe the distribution of the dependent variable conditional on the predictor variable。使用简单线性回归模型有几个前提假设:
- 因变量对预测变量的条件分布的方差是保持不变的 the variance of the dependent variable (conditional on the predictor variable) is constant。
- 该条件分布是一个正态分布。
有时候,这些假设条件并不能得到满足。上面的散点图23.1看上去还算符合这两个假设前提:在每一个年龄阶段,体重的分布没有发生歪斜(skew),分散分布(方差) 也相对稳定。但是图 23.4 中的价格-克拉数据很明显无法满足上面的前提假设。在线性回归模型中,我们使用 \(\sigma^2\) 表示残差的方差 (residual variance)。
library(ggplot2)
library(ggthemes)
ggplot(data=diamonds, aes(x=carat, y=price)) + geom_point(shape=20)+
theme_stata()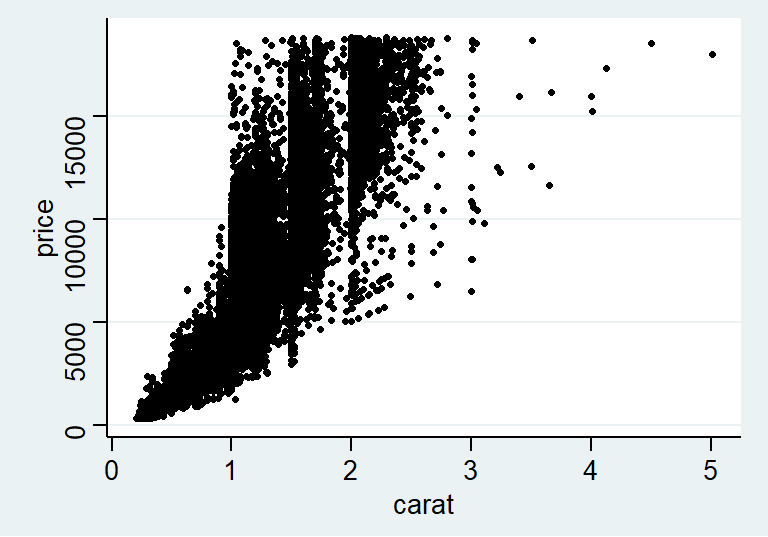
图 23.4: Relationship between diamond carat and price
23.3.3 定义简单线性回归模型
用来描述一个随机变量 \((Y)\) 和另一个变量 \((X)\) 之间关系的简单线性回归模型,被定义为:
\[ (Y|X=x) \sim N(\alpha+\beta x, \sigma^2) \]
上面这个模型,同时还描述了我们对数据的分布的假设。同样的模型,你可能更多得看到被写成如下的方式:
\[ y=\alpha+\beta x+ \varepsilon \text{, where } \varepsilon\sim N(0,\sigma^2) \]
假如,我们有一组样本量为 \(n\) 的数据 \(\underline{x}\)。我们就可以把通过上面的回归模型实现的 \(Y_i\) 和它对应的 \(X_i (i=1,\cdots, n)\)。描述为如下的形式:
\[ \begin{equation} (Y_i|X_i=x_i) \sim \text{NID}(\alpha+\beta x, \sigma^2) \text{ where } i=1,\cdots,n \end{equation} \tag{23.1} \]
此处的 \(\text{NID}\) 意为独立且服从正态分布 (normally and independently distributed)。这里默认的一个重要前提是所有的观察值 \(X_i\) 是相互独立互不影响的。例如上面图 23.1 所示儿童的年龄和体重数据,就必须假设这些儿童都来自没有血缘关系的独立家庭。如果这以数据中的儿童,有些是兄弟姐妹的话,观察数据互相独立的前提就无法得到满足。不满足相互独立前提的数据,其分析方法会在 “Analysis of hierarchical and other dependent data (Term 2)” 中详尽介绍。
公式 (23.1) 常被记为:
\[ \begin{equation} (Y_i|X_i=x_i) = \alpha + \beta x_i + \varepsilon_i, \text{ where } \varepsilon_i\sim \text{NID}(0,\sigma^2) \end{equation} \tag{23.2} \]
或者为了简洁表述写成:
\[ \begin{equation} y_i = \alpha + \beta x_i + \varepsilon_i, \text{ where } \varepsilon_i\sim \text{NID}(0,\sigma^2) \end{equation} \tag{23.3} \]
23.3.4 残差 residuals
公式 (23.2) 和 (23.3) 其实已经包含了残差的表达式:
\[ \varepsilon_i = y_i - (\alpha + \beta x_i) \]
所以 \(\varepsilon_i\) 的意义是第 \(i\) 个观察对象的随机(偶然)误差 (random error),或者叫真实残差 (true residual)。其实就是从线性回归模型计算获得的映射值 \(\alpha+\beta x_i\),和实际观察值 \(y_i\) 之间的差距。而且从其公式可见,残差本身也是由人群的参数 \((\alpha, \beta)\) 决定的。残差也被定义为回归模型的偏差值。当我们用样本数据获得的参数估计\((\hat\alpha, \hat\beta)\) 来取代掉参数\((\alpha, \beta)\) 时,这时的模型变成了估计模型,残差也成了估计残差或者叫观察模型和观察残差。须和真实残差加以区分。
23.4 参数的估计
简单线性回归模型中有三个人群参数 \((\alpha, \beta, \sigma^2)\)。统计分析的目标,就是使用样本数据 \(Y_i, X_i, (i=1, \cdots, n)\) 来对总体参数做出推断 (inference)。在线性回归中主要使用普通最小二乘法 (ordinary least squares, OLS) 作为推断的工具。在统计学中,我们习惯给希腊字母戴上“帽子”,作为该参数的估计值,例如 \(\hat\alpha, \hat\beta\) 是参数 \(\alpha, \beta\) 的估计值。通过线性回归模型,给第 \(i\) 个观察值拟合的预测值,被叫做因变量的估计期望值 (estimated expectation)。用下面的式子来表示:
\[ \hat{y}_i=\hat\alpha+\hat\beta x_i \]
此时,第 \(i\) 名对象的观察残差 (observed or fitted or estimated residuals) 用下面的式子来表示:
\[ \hat{\varepsilon}_i = y_i-\hat{y}_i=y_i-(\hat\alpha+\hat\beta x_i) \]
23.4.1 普通最小二乘法估计 \(\alpha, \beta\)
普通最小二乘法估计的 \(\alpha, \beta\) 会最小化拟合回归直线的偏差 minimize the sum of squared deviations from the fitted regression line。其正式的定义为:OLS估计值,指的是能够使残差平方和(residual sum of squares, \(SS_{RES}\))取最小值的$, $。
\[ \begin{equation} SS_{RES} = \sum_{i=1}^n \hat{\varepsilon}^2_i = \sum_{i=1}^n (y_i-\hat\alpha-\hat\beta x_i)^2 \end{equation} \tag{23.4} \]
可以证明的是,OLS的 \(\alpha, \beta\) 估计值的计算公式为:
\[ \begin{equation} \hat\alpha=\bar{y}-\hat\beta\bar{x} \tag{23.5} \end{equation} \]
\[ \begin{equation} \hat\beta=\frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n(x_i-\ bar{x})^2} \tag{23.6} \end{equation} \]
其中 \(\bar{y}=\frac{\sum_{i=1}^ny_i}{n}, \bar{x}=\frac{\sum_{i=1}^nx_i}{n}\)
证明
求能最小化\(SS_{RES}\) 的\(\alpha\), 我们需要把公式(23.4) 对\(\hat\alpha\) 求导,然后将求导之后的式子等于\(0\) 之后求根即可:
\[ \begin{aligned} & \frac{\text{d}SS_{RES}}{\text{d}\hat\alpha} =\sum_{i=1}^n -2(y_i-\hat\alpha-\hat\beta x_i ) = 0\\ & \text{Since } \sum_{i=1}^n(y_i) = n\bar{y}; \sum_{i=1}^n (x_i) =n\bar{x} \\ & \Rightarrow -n\bar{y}+n\hat\alpha+n\hat\beta\bar{x} = 0 \\ & \Rightarrow \hat\alpha = \bar{y}-\hat\beta\bar{x} \end{aligned} \]
求能最小化 \(SS_{RES}\) 的 \(\beta\),求导之前我们先把公式 (23.4) 中含有 \(\hat\alpha\) 的部分替换掉:
\[ \begin{equation} \begin{split} SS_{RES} &= \sum_{i=1}^n\hat\varepsilon_i^2=\sum_{i=1}^n(y_i-(\bar{y}-\hat\beta\bar{x} )-\hat\beta x_i)^2\\ &= \sum_{i=1}^n((y_i-\bar{y})-\hat\beta(x_i-\bar{x}))^2 \\ \end{split} \tag{23.7} \end{equation} \]
接下来对上式 (23.7) 求导之后,用相同办法求根:
\[ \begin{aligned} &\frac{\mathrm{d} SS_{RES}}{\mathrm{d} \hat\beta} = \sum_{i=1}^n -2(x_i-\bar{x})(y_i-\ bar{y}) + 2\hat\beta(x_i-\bar{x})^2 = 0\\ & \Rightarrow \hat\beta\sum_{i=1}^n(x_i-\bar{x})^2 = \sum_{i=1}^n (x_i-\bar{x})(y_i-\ bar{y}) \\ & \hat\beta=\frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n(x_i- \bar{x})^2} \end{aligned} \]
23.5 残差方差的估计 \((\sigma^2)\)
残差方差等于残差平方和除以样本量。所以我们会把残差方差的估计用下面的式子表示:
\[ \begin{equation} \hat\sigma^2=\sum_{i=1}^n \frac{\hat\varepsilon^2}{n} = \sum_{i=1}^n \frac{(y_i-\hat\alpha- \hat\beta x_i)^2}{n} \end{equation} \tag{23.8} \]
这的确是 \(\sigma^2\) 的极大似然估计 (MLE)。然而我们知道,公式 (23.8) 并不是残差方差的无偏估计。类似与样本方差低估了总体方差 (Section 10.3),那样,这里残差方差的观察值也是低估了总体残差方差的。所以,残差方差的无偏估计需要用下面的式子来校正:
\[ \begin{equation} \hat\sigma^2=\sum_{i=1}^n \frac{\hat\varepsilon^2}{n-2} = \sum_{i=1}^n \frac{(y_i-\hat\ alpha-\hat\beta x_i)^2}{n-2} \end{equation} \tag{23.9} \]
公式 (23.9) 被叫做残差均方 (Residual Mean Squares, RMS),常常被标记为 \(\text{MS}_{RES}\)。分母的 \(n-2\),表示进行残差方差估计时用掉了两个信息量 \(\alpha, \beta\) (自由度减少了 2)。
23.6 R 演示 例 1: 图 23.1 数据
library(haven)
growgam1 <- read_dta("../Datas/growgam1.dta")
slm <- lm(wt~age, data=growgam1)
summary(slm) # basic default output of the summary##
## Call:
## lm(formula = wt ~ age, data = growgam1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.9242 -0.7849 0.0071 0.7975 4.0678
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.83758 0.21007 32.55 <2e-16 ***
## age 0.16533 0.01111 14.88 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.274 on 188 degrees of freedom
## Multiple R-squared: 0.5408, Adjusted R-squared: 0.5383
## F-statistic: 221.4 on 1 and 188 DF, p-value: < 2.2e-16## Analysis of Variance Table
##
## Response: wt
## Df Sum Sq Mean Sq F value Pr(>F)
## age 1 359.06320 359.06320 221.39203 < 2.22e-16 ***
## Residuals 188 304.90655 1.62184
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1也可以用 stargazer 包输出很酷的表格报告:
| Dependent variable: | |
| wt | |
| age | 0.165*** |
| (0.011) | |
| Constant | 6.838*** |
| (0.210) | |
| Observations | 190 |
| R2 | 0.541 |
| Adjusted R2 | 0.538 |
| Residual Std. Error | 1.274 (df = 188) |
| F Statistic | 221.392*** (df = 1; 188) |
| Note: | p<0.1; p<0.05; p<0.01 |
其实结果都一样。我们这里详细来看 \(\alpha, \beta, \sigma^2\):
\(\hat\alpha = 6.84\):当年龄为 \(0\) 时,体重为 \(6.84 kg\)。本数据 23.1 中并没有 \(0\) 岁的儿童,所以这里的截距的解释需要非常小心是否合理。
\(\hat\beta = 0.165\):这数据中儿童的体重估计随着年龄升高 \(1\) 个月增长 \(0.165 kg\)。所以使用这两个估计值我们就可以来估计任意年龄时儿童的体重。图 23.2 就是拟合数据以后的简单线性回归曲线。
\(\hat\sigma^2 = 1.62, \hat\sigma=1.27\) 就是默认输出中最下面的 Residual standard error: 1.274 和 ANOVA 表格中 Residuals 的 Mean Sq=1.62184 部分。含义是,沿着拟合的直线,在每一个给定的年龄上儿童体重的分布的标准差是 \(1.27 kg\)。
23.7 R 演示 例 2: 表23.1 数据
在R里面不需要自己生成哑变量 (dummy variables)。R中,分类变量被设置成因子 “factor” 时,你就完全可以忽略生成哑变量的过程。下图 23.5 显示了两组儿童直立行走时的年龄。
library(ggplot2)
library(ggthemes)
dt <- read.csv("../Datas/walking.csv", header = T)
age1 <- dt$Active.Exercise.Group..n.6.
age2 <- dt$Eight.Week.Control.Group..n.5.
Group <- c(rep("exercise", 6), rep("control", 6))
Walk <- data.frame(c(age1,age2), Group)
names(Walk)[1] <- "Age"
## Reordering Group
Walk$Group <- factor(Walk$Group,levels=c("exercise", "control"))
ggplot(Walk, aes(x=Group, y=Age)) + geom_point() +
scale_y_continuous(breaks = seq(9, 14, 1),limits = c(9,14)) +
theme_stata() +labs(x = "Randomised groups", y = "Age (Months)")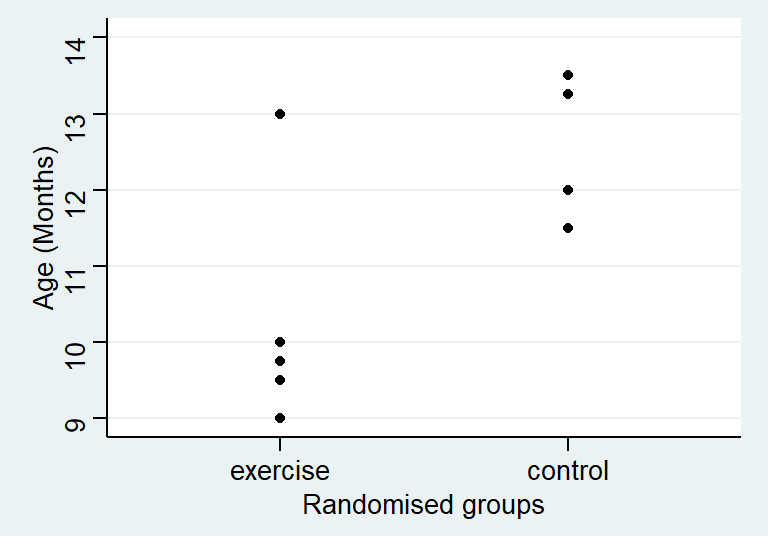
图 23.5: Age at walking by group
拟合简单线性回归也是小菜一碟:
##
## Call:
## lm(formula = Age ~ Group, data = Walk)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.1250 -0.7375 -0.3750 0.3875 2.8750
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.1250 0.5122 19.766 1.01e-08 ***
## Groupcontrol 2.2250 0.7598 2.929 0.0168 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.255 on 9 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.4879, Adjusted R-squared: 0.4311
## F-statistic: 8.576 on 1 and 9 DF, p-value: 0.0168## Analysis of Variance Table
##
## Response: Age
## Df Sum Sq Mean Sq F value Pr(>F)
## Group 1 13.502 13.5017 8.5763 0.0168 *
## Residuals 9 14.169 1.5743
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1这里的\(\hat\alpha=10.125\),意为参照组(此处,“exercise” 被默认设定为参照组,而”control” 被默认拿来和参照组相比较) 的儿童也就是,积极练习走路的小朋友这组能够独立行走的平均年龄是\(10.125\) 个月。
\(\hat\beta=2.225\),意为和参照组 (积极练习组) 相比,对照组儿童能够自己行走的年龄平均要晚 \(2.225\) 个月。所以对照组儿童能够直立行走的平均年龄就是 \(10.125+2.225=12.35\) 个月。
上述结果,你如果拿来和下面的两样本 \(t\) 检验的结果相比就知道,是完全一致的。其中统计量 \(t^2=2.9285^2=F_{1,9}=8.58\)。
##
## Two Sample t-test
##
## data: Age by Group
## t = -2.9285, df = 9, p-value = 0.0168
## alternative hypothesis: true difference in means between group exercise and group control is not equal to 0
## 95 percent confidence interval:
## -3.9437116 -0.5062884
## sample estimates:
## mean in group exercise mean in group control
## 10.125 12.35023.8 实例
使用的数据内容为:两次调查同一样本,99 名健康男性的血清胆固醇水平,间隔一年。
## id chol1 chol2
## Min. : 1.0 Min. :152.0 Min. :170.0
## 1st Qu.:25.5 1st Qu.:235.0 1st Qu.:240.0
## Median :50.0 Median :265.0 Median :260.0
## Mean :50.0 Mean :264.6 Mean :263.5
## 3rd Qu.:74.5 3rd Qu.:290.0 3rd Qu.:290.0
## Max. :99.0 Max. :360.0 Max. :355.0## vars n mean sd median trimmed mad min max range skew kurtosis
## id 1 99 50.00 28.72 50 50.00 37.06 1 99 98 0.00 -1.24
## chol1 2 99 264.59 40.76 265 264.52 40.03 152 360 208 -0.09 -0.13
## chol2 3 99 263.54 38.17 260 262.84 37.06 170 355 185 0.17 -0.27
## se
## id 2.89
## chol1 4.10
## chol2 3.84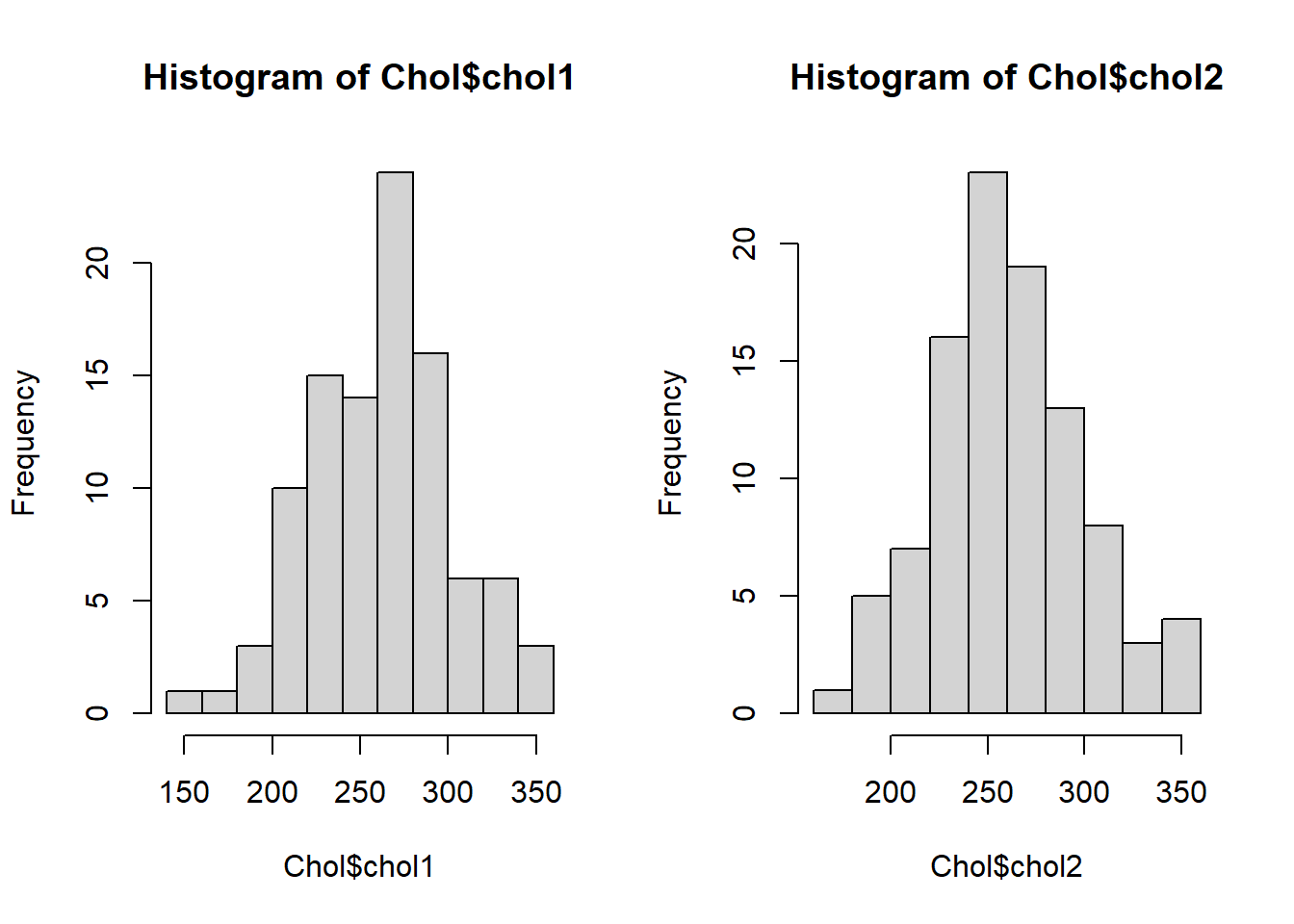
# 对两次胆固醇水平作散点图
ggplot(Chol, aes(x=chol1, y=chol2)) + geom_point(shape=20) +
scale_x_continuous(breaks=seq(150, 400, 50),limits = c(150, 355))+
scale_y_continuous(breaks=seq(150, 400, 50),limits = c(150, 355)) +
theme_stata() +labs(x = "Cholesterol at visit 1 (mg/100ml)", y = "Cholesterol at visit 2 (mg/100ml)")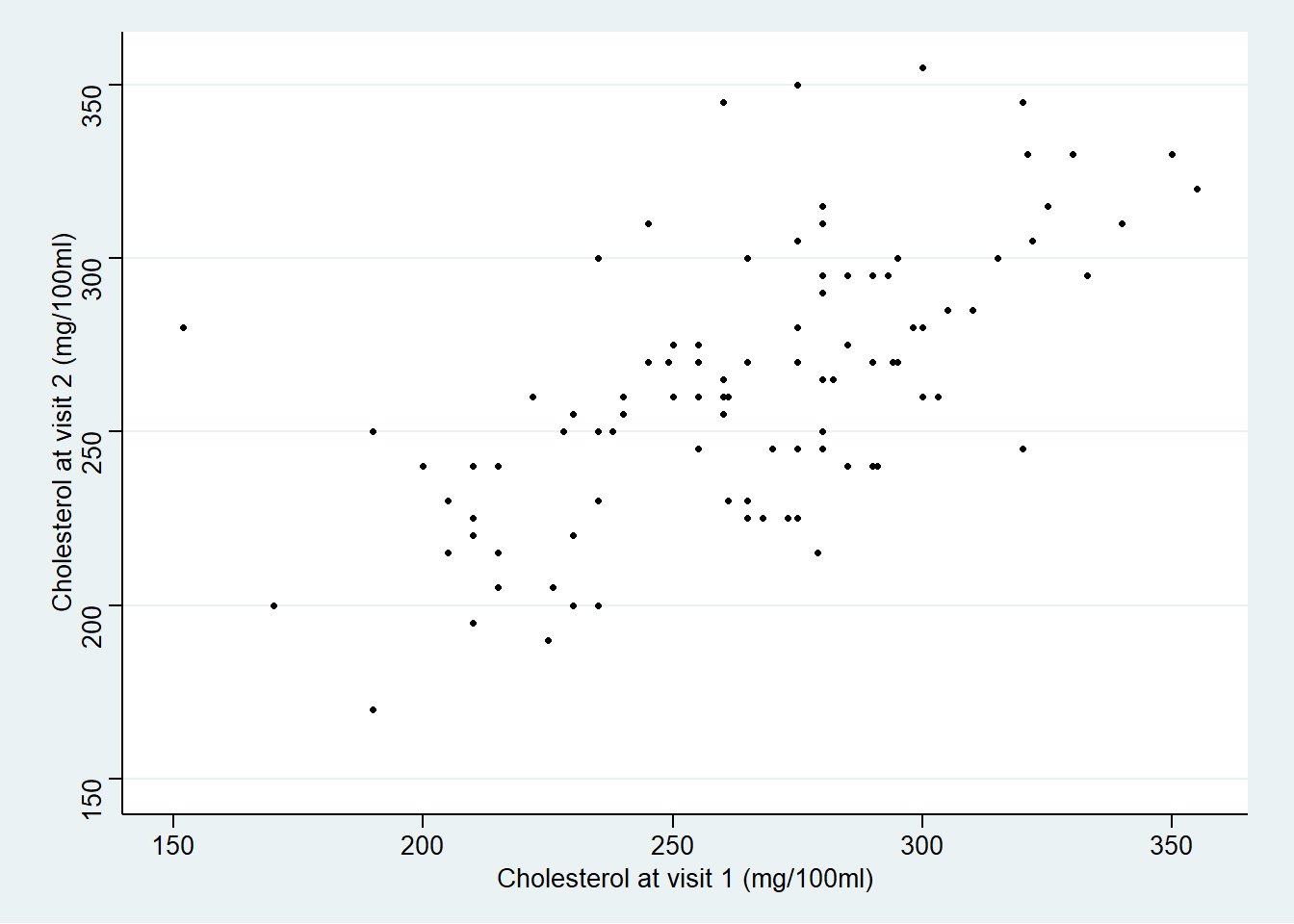
两次测量的胆固醇水平分别用 \(C_1, C_2\) 来标记的话,考虑这样的简单线性回归模型:\(C_2=\alpha+\beta C_2 + \varepsilon\)。我们进行这样回归的前提假设有哪些?
- 每个观察对象互相独立。
- 前后两次测量的胆固醇水平呈线性相关。
- 残差值,在每一个给定的 \(C_1\) 值处呈现正态分布,且方差不变。
从散点图来看这些假设应该都能得到满足。
## [1] 264.5859## [1] 263.5354## [1] 1661.061## [1] 1456.761## [1] 961.22423.8.1 计算普通最小二乘法 (OLS) 下,截距和斜率的估计值 \(\hat\alpha, \hat\beta\)
\[ \begin{aligned} \hat\beta &= \frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n(x_i- \bar{x})^2}\\ &=\frac{\text{Cov}(C_1,C_2)}{\text{Var}(C_1)}\\ &=\frac{1661.061}{961.224}=0.578 \end{aligned} \]
## [1] 0.5786806\[\hat\alpha=\bar{y}-\hat\beta\bar{x}=263.54-0.578\times264.59=110.425\]
## [1] 110.424723.8.2 和回归模型计算的结果作比较,解释这些估计值的含义
##
## Call:
## lm(formula = chol2 ~ chol1, data = Chol)
##
## Residuals:
## Min 1Q Median 3Q Max
## -56.877 -22.062 1.849 16.631 84.118
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 110.42466 20.01133 5.518 2.85e-07 ***
## chol1 0.57868 0.07476 7.741 9.51e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 30.16 on 97 degrees of freedom
## Multiple R-squared: 0.3818, Adjusted R-squared: 0.3755
## F-statistic: 59.92 on 1 and 97 DF, p-value: 9.511e-12- 截距的估计值是 110.4 mg/100ml: 意为这组样本,第一次采集数据时,胆固醇水平的平均值是 110.4。
- 斜率的估计值是 0.58:意为第一次采集的胆固醇水平每高 1 mg/100ml,那么第二次采集的胆固醇相应提高的值的期待量为 0.58.
23.8.3 加上计算的估计值直线 (即回归直线)
ggplot(Chol, aes(x=chol1, y=chol2)) + geom_point(shape=20, colour="grey40") +
stat_smooth(method = lm, se=FALSE, size=0.5) +
scale_x_continuous(breaks=seq(150, 400, 50),limits = c(150, 355))+
scale_y_continuous(breaks=seq(150, 400, 50),limits = c(150, 355)) +
theme_stata() +labs(x = "Cholesterol at visit 1 (mg/100ml)", y = "Cholesterol at visit 2 (mg/100ml)")## `geom_smooth()` using formula = 'y ~ x'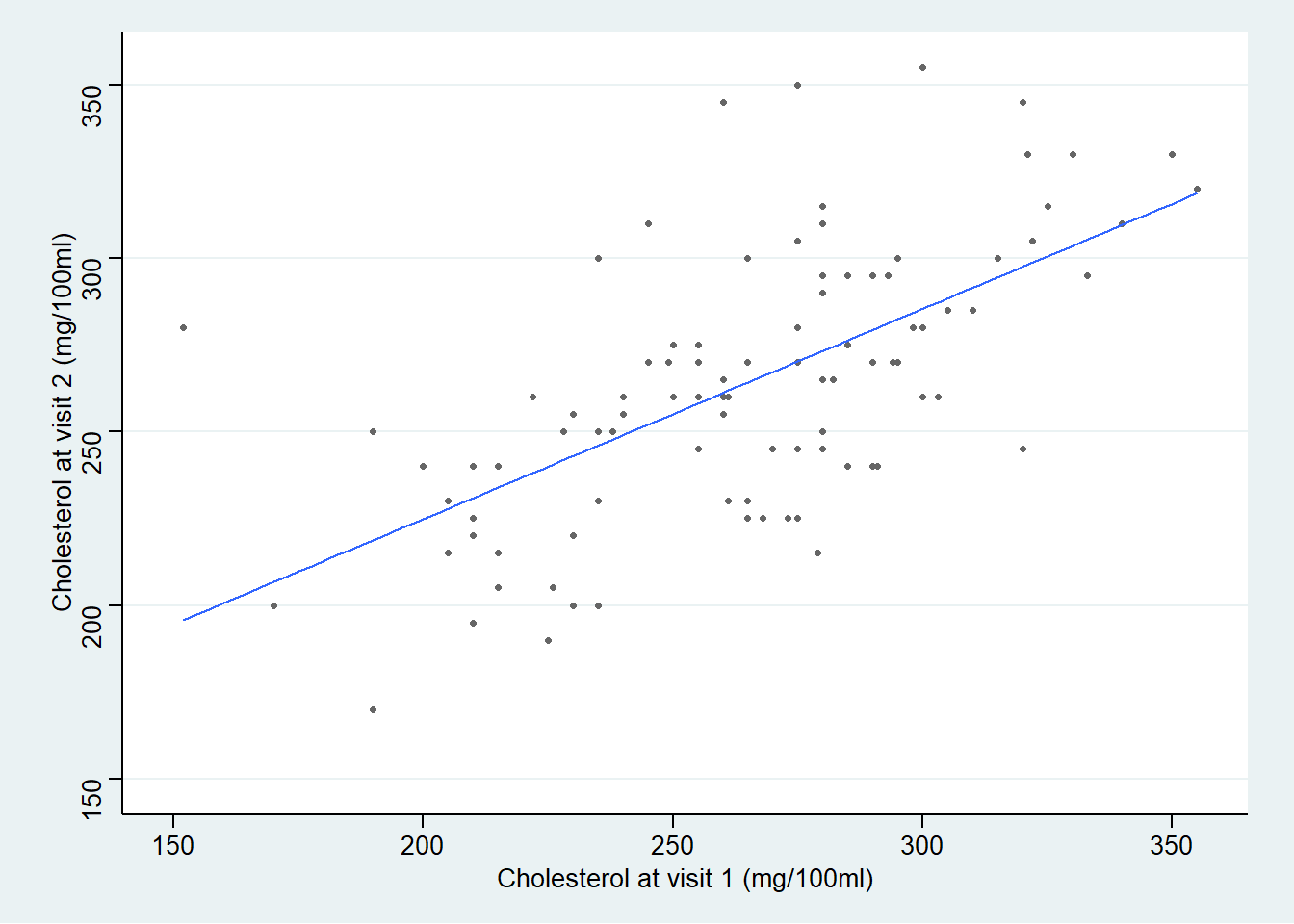
可以注意到,第一次访问时胆固醇水平高的人,第二次被测量时胆固醇值高于平均值,但是却没有第一次高出平均值的部分多。 相似的,第一次胆固醇水平低的人,第二次胆固醇水平低于平均值,但是却没有第一次低于平均值的部分多。这一现象被叫做 “向均数回归-regression to the mean”
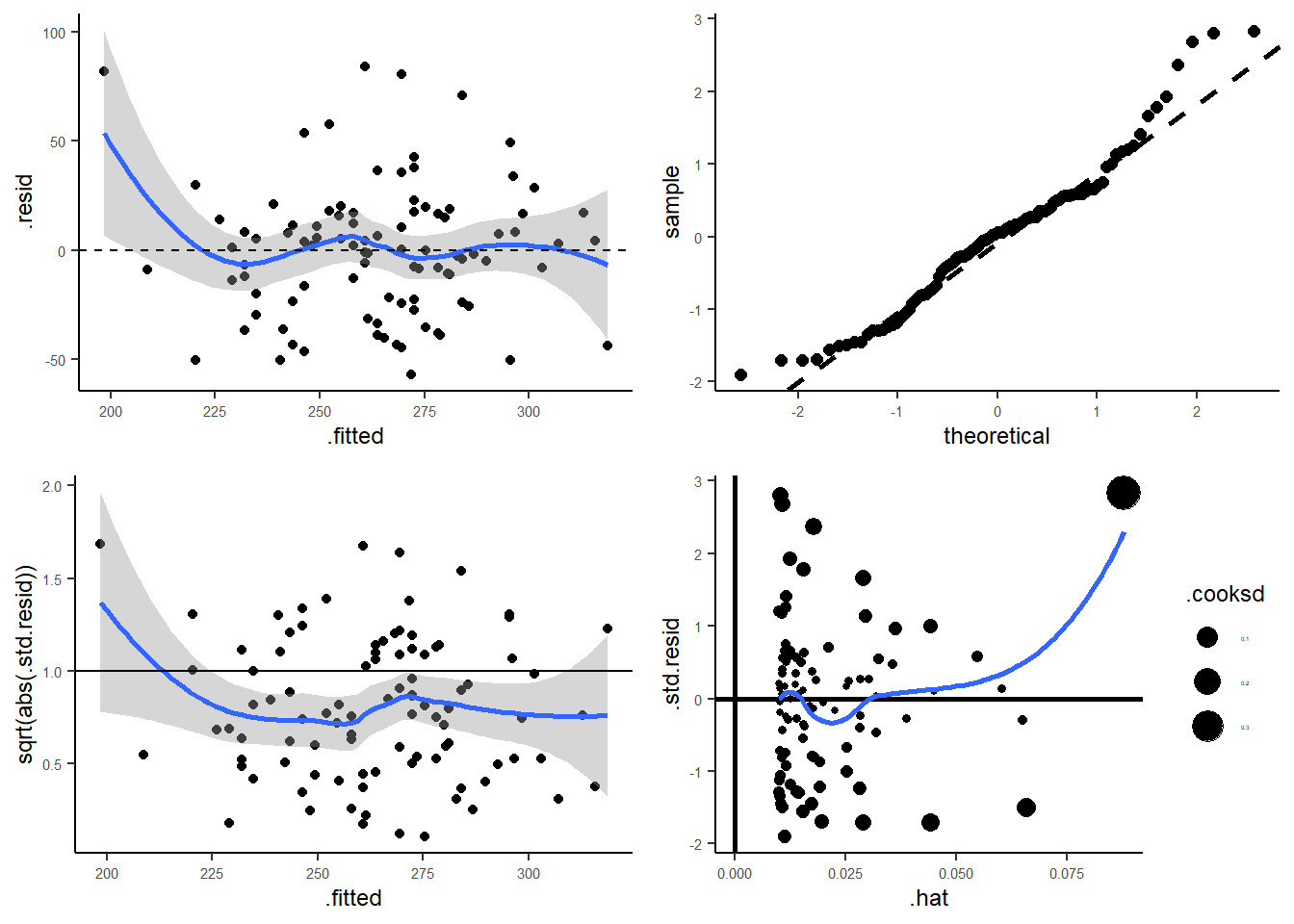
23.8.4 下面的代码用于模型的假设诊断
M <- lm(chol2~chol1, data=Chol)
par(mfrow = c(2, 2)) # Split the plotting panel into a 2 x 2 grid
plot(M)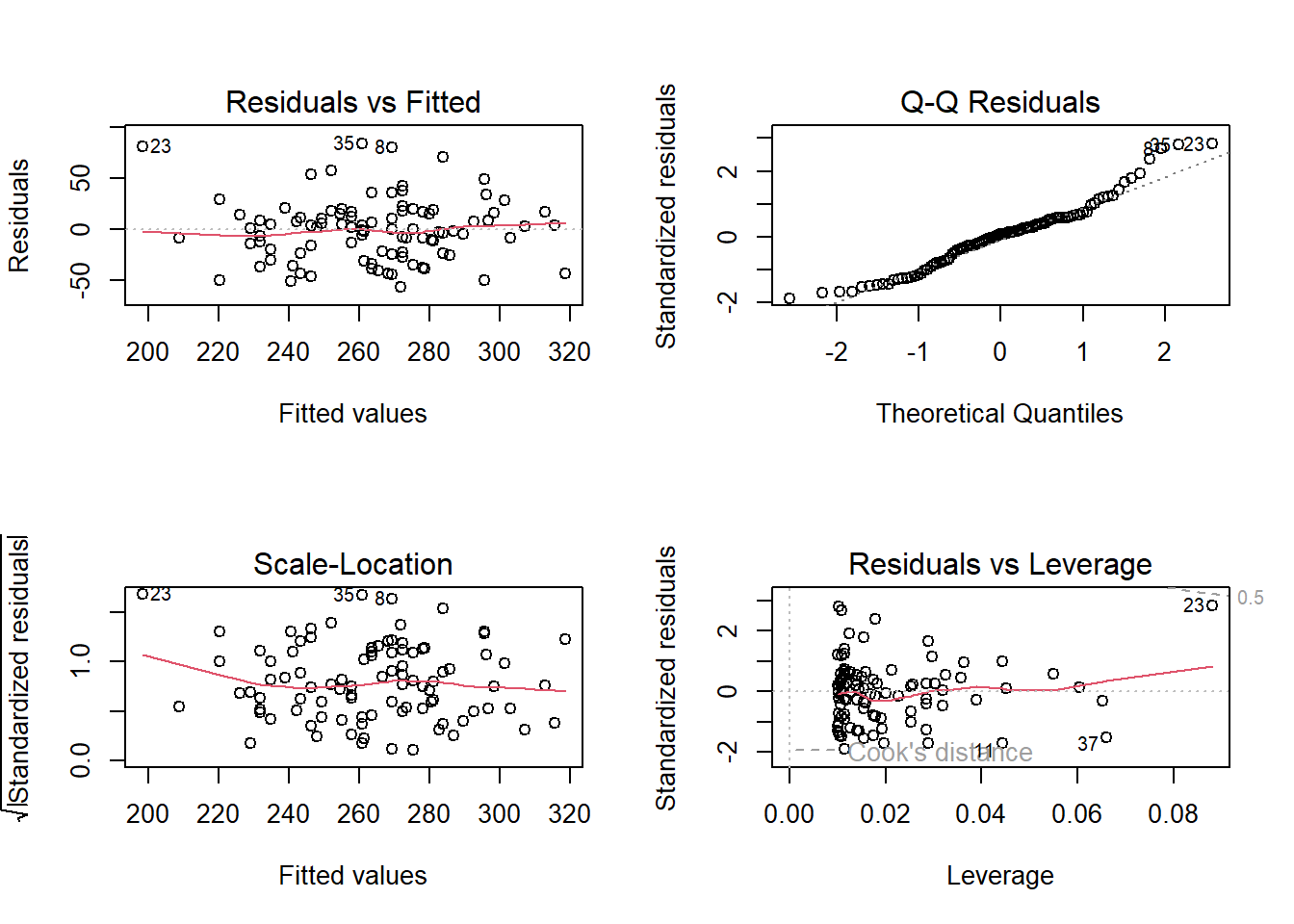
在 github 上共享了 Check_assumption.R 的代码,可以使用 ggplot2 来获取高逼格的模型诊断图: