第 7 章 正态分布

7.1 概率密度曲线

• 一个随机连续型变量 \(X\) 它的性质由一个对应的概率密度方程 (probability density function, PDF) 决定。

• 在给定的范围区间内，如 \(a\sim b, (a < b)\)，它的概率满足:

\[P(a\leqslant X \leqslant b) = \int_a^bf(x)dx\]

• 这个相关的方程，在 \(a\sim b\) 区间内的积分，就是这个连续变量在这个区间内取值的概率。

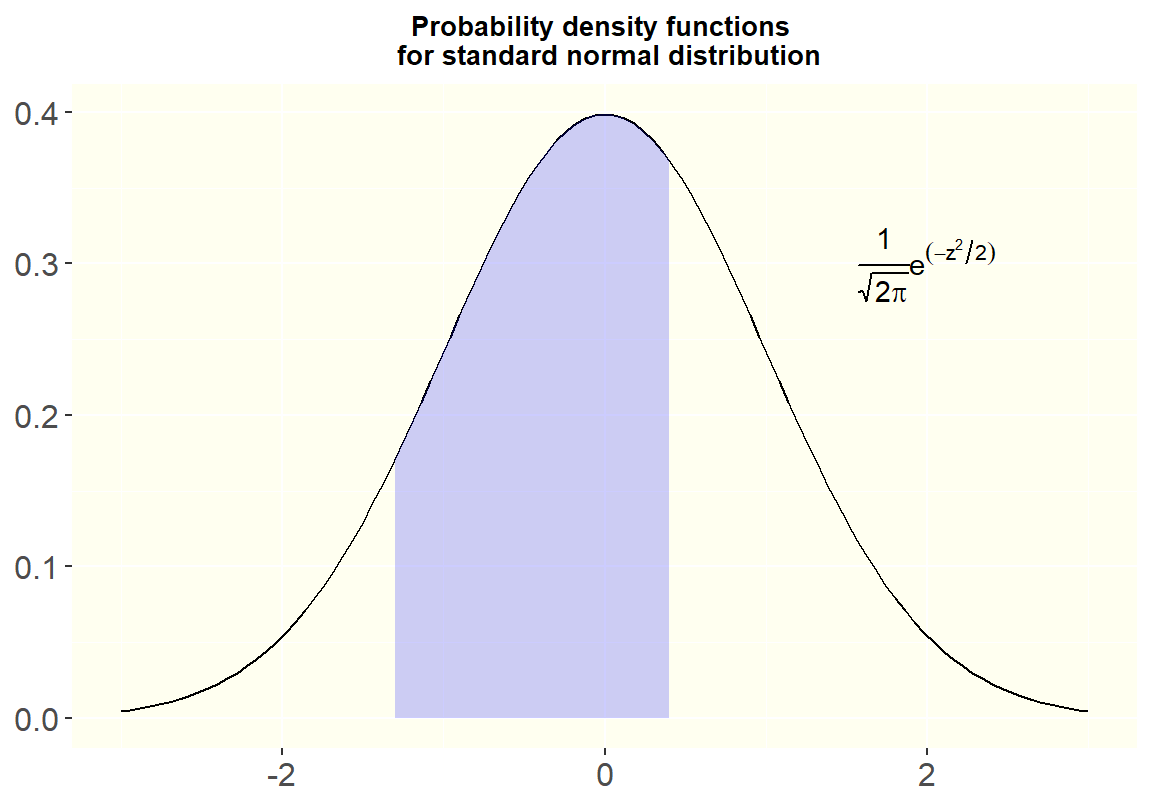
图 7.1: Probability Density Function of a Standard Normal Distribution

注意：整个方程的曲线下面积等于 \(1\)： \[\int_{-\infty}^\infty f(x)dx=1\]

• 期望 \(E(X)=\int_{-\infty}^\infty xf(x)dx\)
• 方差 \(Var(X)=\int_{-\infty}^\infty (x-\mu)^2f(x)dx\)

7.2 正态分布

如果一组数据服从正态分布，我们通常用它的期望（或者叫平均值）\(\mu\)，和它的方差 \(\sigma^2\)，来描述这组数据。记为：

\[X \sim N(\mu, \sigma^2)\]

• 它的概率密度方程可以表述为：

\[f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{(x-\mu)^2}{2\sigma^2})\]

• \(E(x) =\mu\)
• \(Var(x)=\sigma^2\)

7.3 标准正态分布

标准正态分布的期望（或者均值）为 \(0\)，方差为 \(1\)

• 记为：\(Z \sim N(0,1)\)
• 它的概率密度方程表述为：

\[\frac{1}{\sqrt{2\pi}}exp(-\frac{z^2}{2})\]

• 它的累积分布方程 (cumulative distribution function， CDF)，是将概率密度方程 (PDF) 积分以后获得的方程。通常我们记为 \(\Phi(z)\)

再看一下标准正态分布的概率密度方程曲线：

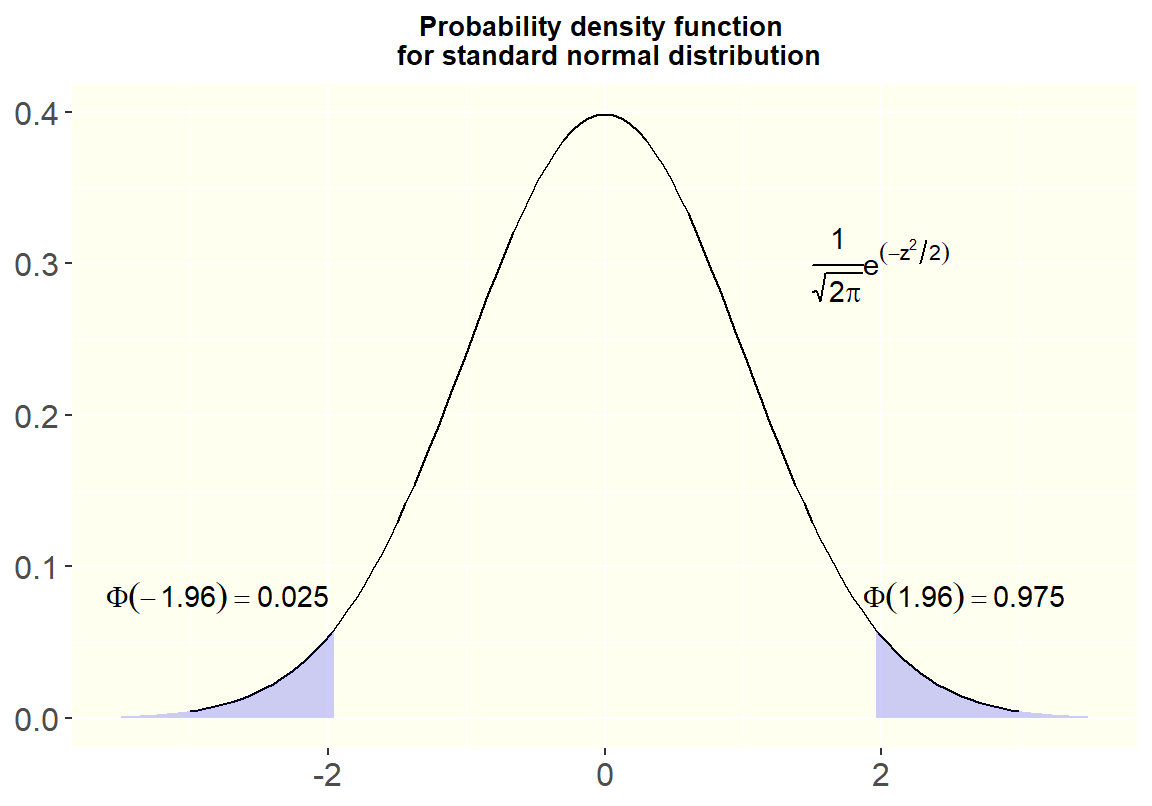
图 7.2: Probability Density function of a Standard Normal Distribution

• 95% 的曲线下面积在标准差 standard deviation \(-1.96\sim1.96\) 之间的区域。
• 而且，\(\phi(-x)=1-\phi(x)\)
• 任何一个正态分布都可以通过下面的公式，标准化成为标准正态分布：

\[Z=\frac{X-\mu}{\sigma}\]