第 21 章 比较
- 本章暂且只讨论两组之间的比较 (均值,方差,百分比);
- 本章也只讨论两种类型的变量,连续型和二分类型变量;
- 本章会介绍点估计 (point estimation),置信区间计算 (confidence intervals),假设检验 (hypothesis testing)。
21.1 比较两个均值
21.1.1 当方差已知,且数据服从正态分布 Z-test
令\(Y_{1i} (i=1,2,\cdots, n_1); Y_{2i} (i=1,2,\cdots, n_2)\) 表示两个独立且随机的变量,他们来自两个人群(1 和2),且各自的人群均值为\(\mu_k\),方差为\(\sigma_k^2\):
\[ E(Y_{ki})=\mu_k \text{ and Var}(Y_{ki}) = \sigma_k^2 \text{ for } k=1,2 \text{ and } i= 1,2,\cdots ,n_k \]
用样本均值 \(\bar{Y}_k\) 作为总体均值 \(\mu_k\) 的估计:
\[ \bar{Y}_k \sim N(\mu_k, \frac{\sigma_k^2}{n_k}) \text{ for } k=1,2 \]
如果两个样本的观察值互相独立,我们知道均值差 \(\bar{Y}_2 - \bar{Y}_1\),也服从下面描述的正态分布:
\[ \begin{equation} \bar{Y}_2-\bar{Y}_1 \sim N(\mu_2-\mu_1, \frac{\sigma^2_2}{n_2}+\frac{\sigma^2_1}{n_1}) \end{equation} \tag{21.1} \]
根据这个性质,可以计算均值差的统计量 \(Z\):
\[ \begin{equation} Z=\frac{\bar{Y}_2-\bar{Y}_1}{\sqrt{(\sigma_2^2/n_2)+(\sigma_1^2)/n_1}} \sim N(\frac{\ mu_2-\mu_1}{\sqrt{(\sigma_2^2/n_2)+(\sigma_1^2)/n_1}},1) \end{equation} \tag{21.2} \]
所以\(\bar{Y}_2-\bar{Y}_1\) 的样本分布(21.2),就可以应用于为\(\mu_2-\mu_1\) 计算显著性水平为$$ 的\(100(1-\alpha)\%\) 置信区间,或者进行假设检验。
用置信区间章节 (Section 18.4) 学到的方法,均值差的置信区间的下限 \(L\),和上限 \(U\),分别是:
\[ \begin{aligned} L & = (\bar{Y}_2 - \bar{Y}_1) + z_{\alpha/2}\sqrt{\frac{\sigma_2^2}{n_2}+\frac{\sigma_1^2}{ n_1}}\\ U & = (\bar{Y}_2 - \bar{Y}_1) + z_{1-\alpha/2}\sqrt{\frac{\sigma_2^2}{n_2}+\frac{\sigma_1^2 }{n_1}} \end{aligned} \]
由于标准正态分布左右对称 \(z_{\alpha/2}=-z_{1-\alpha/2}\),所以\(100(1-\alpha)\%\) 置信区间为:
\[ \begin{equation} (\bar{Y}_2 - \bar{Y}_1) \pm z_{1-\alpha/2}\sqrt{\frac{\sigma_2^2}{n_2}+\frac{\sigma_1^2}{ n_1}} \end{equation} \tag{21.3} \]
进行均值差的假设检验时,零假设是均值差等于零\(\text{H}_0: \mu_2-\mu_1 = 0\);替代假设是均值差不等于零\(\text{H}_1: \mu_2-\ mu_1\neq0\)。
在零假设条件下\(\mu_2-\mu_1 = 0\),公式(21.2) 计算的均值差的检验统计量\(Z\) 服从标准正态分布\(Z\sim N(0, 1)\)。根据章节 19.3.2 同理知双侧 \(p\) 值的计算式为:
\[ \begin{equation} 2[1-\Phi(\frac{|\bar{y}_2-\bar{y}_1|}{\sqrt{(\sigma_2^2/n_2)+(\sigma_1^2/n_1)}}) ] \end{equation} \tag{21.4} \]
此时,我们进行的假设检验,计算的置信区间用到的前提有:
- 两组的观察数据 \(Y_{ki}\) 均服从正态分布;
- 所有的观察对象互相独立;
- 两组数据来自的人群的方差已知。
违反这些前提的话: 1. 如果不满足前提 1,对统计结果影响不会很大,只要观察样本较大,均值或者均值差本身的样本分布也就服从了正态分布 (中心极限定理); 2. 如果不满足前提 2,则不应该采用此方法,观察对象本身如果有一定的结构构成或者不满足相互独立,本方法不适用; 3. 前提3,大多数现实例子中都不太可能满足,因为总体/人群的方差多数情况下都是未知的,所以,下一小节讨论方差未知的情况,逐渐放宽我们的统计分析前提条件。
21.1.2 当方差未知,但是方差可以被认为相等,且数据服从正态分布 two sample \(t\) test
如果两组数据来自的人群可以被认为方差是齐的 \(\sigma_1^2=\sigma_2^2=\sigma^2\),公式 (21.1) 可以变为:
\[ \bar{Y}_2-\bar{Y}_1 \sim N(\mu_2-\mu_1, \sigma^2(\frac{1}{n_2}+\frac{1}{n_1})) \]
但是这个分布中的方差是未知的,所以除了均值和均值差,这个共同的方差也变成了需要用样本方差 \(\hat{\sigma}^2\) 来作估计。此时,两个样本的方差的无偏估计为,加权方差:
\[ \begin{equation} \hat\sigma^2 = \frac{(n_1-1)\hat\sigma^2_1+(n_2-1)\hat\sigma^2_2}{n_1+n_2-2} \end{equation} \tag{21.5} \]
因为\(\frac{(n_1-1)\hat\sigma^2_1}{\sigma^2} \sim \chi^2_{n_1-1}; \frac{(n_2-1)\hat\sigma^2_2} {\sigma^2} \sim \chi^2_{n_2-1}\),所以两样本的加权方差\(\hat\sigma^2\) 服从自由度为\(n_1+n_2-2\) 的卡方分布:
\[ \frac{(n_1+n_2-2)\hat\sigma^2_1}{\sigma^2} \sim \chi^2_{n_1+n_2-2} \]
所以,此时的检验统计量 \(T\),服从自由度为 \(n_1+n_2-2\) 的 \(t\) 分布:
\[ T=\frac{(\bar{Y}_2-\bar{Y}_1) - (\mu_2-\mu_1)}{\hat\sigma\sqrt{(1/n_2)+(1/n_1)}} \sim t_{n_1+n_2-2} \]
接下来就可以利用这个统计量进行假设检验,求均值差的 \(100(1-\alpha)\%\) 置信区间,类比章节 18.5:
\[ (\bar{Y}_2-\bar{Y}_1) \pm t_{n_1+n_2-2, 1-\alpha/2}\hat\sigma\sqrt{(1/n_2)+(1/n_1) } \]
练习
下表展示的是,随机将11名婴儿分配到实验组和对照组,记录婴儿能够独立行走的月龄。试用表格总结的数据进行能独立行走的月龄的均值是否在实验组和对照组之间有差异的假设检验,并求月龄均差的 \(95\%\) 置信区间。
| Active exercise group (i=1) | Eight week control group (i=2) | |
|---|---|---|
| 9.00, 9.50, 9.75, 10.00, 13.00, 9.50 | 13.25, 11.50, 12.00, 13.50, 11.50 | |
| \(n_i\) | 6 | 5 |
| \(\bar{Y}_i\) | 10.125 | 12.350 |
| \(\hat\sigma_i\) | 1.447 | 0.962 |
解
假设 \(\text{H}_0: \mu_2-\mu_1 = 0 \text{ v.s } \text{H}_1: \mu_2-\mu_1 \neq 0\)
假如,实验组对照组的月龄方差可以认为是方差相同的,那么他们的加权方差则可以计算为:
\[ \hat\sigma^2 = \frac{(6-1)\times(1.447)^2+(5-1)\times(0.962)^2}{6+5-2} = \frac{14.172}{ 9} = 1.575 \]
零假设条件下,则检验统计量 \(T\) 服从自由度为 \(9\) 的 \(t\) 分布,本例的数据给出的检验统计量大小为:
\[ T=\frac{12.350-10.125}{\sqrt{1.575\times(1/5+1/6)}} = \frac{2.225}{0.76} = 2.928 \]
通过查阅统计数据表格:
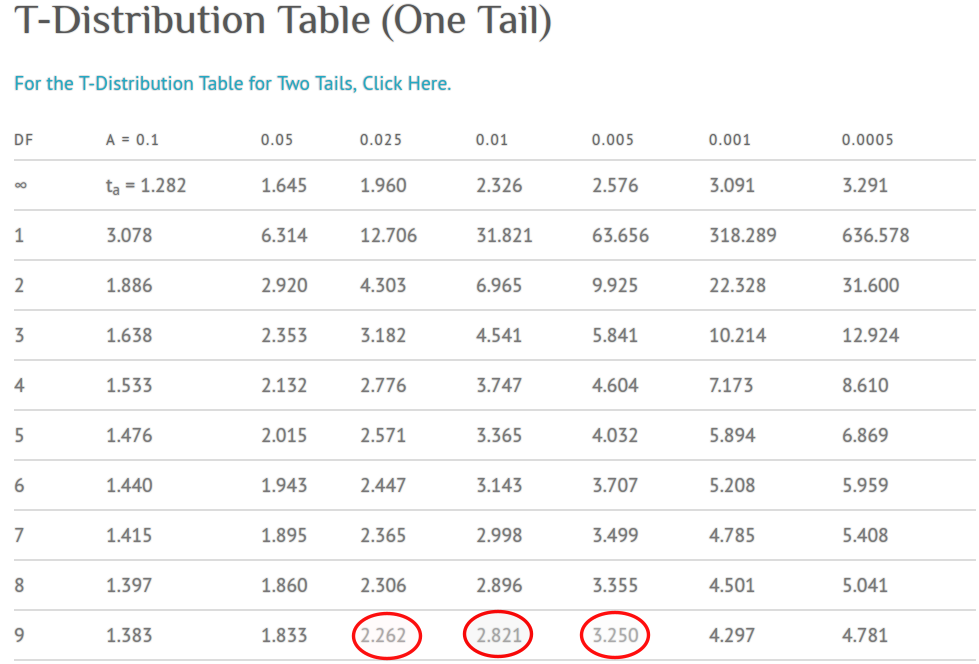
图 21.1: T-Distribution table (0ne-Tail)
图21.1 中显示统计量\(t=2.928\) 的单侧\(p\) 值介于\(0.01\sim0.005\) 之间,所以此例的双侧\(0.01 < p < 0.02\) 。
均值差 \(\mu_2-\mu_1\) 的 \(95\%\) 置信区间为:
\[ \begin{aligned} (\bar{Y}_2-\bar{Y}_1) &\pm t_{9, 0.975}\hat\sigma\sqrt{(1/n_2)+(1/n_1)} \\ = 2.225 &\pm 2.262 \times 0.76 = (0.51, 3.94) \end{aligned} \]
上面的手计算过程,如果你像我一样运气好可能在考场上碰到,实际生活中我们肯定是使用 R 进行计算拉。下面用了两种不同的代码,但是结果和目的都是一样的: t.test() 时指定 var.equal = TRUE或者用简单线性回归的代码 lm()。
##
## Two Sample t-test
##
## data: Walk$Age by Walk$Group
## t = -2.9285, df = 9, p-value = 0.0168
## alternative hypothesis: true difference in means between group exercise and group control is not equal to 0
## 95 percent confidence interval:
## -3.9437116 -0.5062884
## sample estimates:
## mean in group exercise mean in group control
## 10.125 12.350##
## Call:
## lm(formula = Age ~ Group, data = Walk)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.1250 -0.7375 -0.3750 0.3875 2.8750
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.1250 0.5122 19.766 1.01e-08 ***
## Groupcontrol 2.2250 0.7598 2.929 0.0168 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.255 on 9 degrees of freedom
## Multiple R-squared: 0.4879, Adjusted R-squared: 0.4311
## F-statistic: 8.576 on 1 and 9 DF, p-value: 0.016821.1.3 当方差未知,但是方差不可以被认为相等,且数据服从正态分布
下一节会讨论如何比较方差是否齐的手段,用于本节分析方法在实际应用时的参考。
当两组连续型正态分布的数据不能被认为方差相同时,有几种方法可以采用。一是将数据通过数学转换 (log-transformed, etc.),人为的把方差的差异缩小以后,使用前一节的齐方差时的均值比较法 (two-sample \(t\) test)。另一种方法是,既然方差不齐,那就用各自的观察数据来估计其方差 \((\hat\sigma_1^2, \hat\sigma_2^2)\)。只要各自的样本量较大\(n_1, n_2\),两组数据均值差\(|\bar{y}_2-\bar{y}_1|\) 除以其合并后的标准误\(\sqrt{\frac{ \hat\sigma_1^2}{n_1}+\frac{\hat\sigma_2^2}{n_2}}\)。利用公式(21.3) 和(21.4),把已知的两组数据各自的方差用样本方差取代之后即可用于计算置信区间,实施假设检验求\(p\) 值。
但是,当两组观察数据的样本量不大时\((< 30)\),根据Welch–Satterthwaite 建议的,估计均值差除以估计标准误服从一个自由度为\(n^*\) 的\(t\) 分布。值得注意的是,这个自由度并非正整数:
\[ n^*=\frac{(\frac{\hat\sigma_1^2}{n_1}+\frac{\hat\sigma_2^2}{n_2})^2}{[\frac{(\hat\sigma_1^ 2/n_1)^2}{n_1-1}] + [\frac{(\hat\sigma_2^2/n_2)^2}{n_2-1}]} \]
在 R 里可以指定 var.equal = TRUE 进行 \(t\) 检验:
##
## Welch Two Sample t-test
##
## data: Walk$Age by Walk$Group
## t = -3.0449, df = 8.6632, p-value = 0.01453
## alternative hypothesis: true difference in means between group exercise and group control is not equal to 0
## 95 percent confidence interval:
## -3.8878619 -0.5621381
## sample estimates:
## mean in group exercise mean in group control
## 10.125 12.350值得注意的是在 R 里面,\(t\) 检验是默认组间方差不齐的,如果你没有指定 var.equal = TRUE,R 就会默认进行上面的方差不齐的 \(t\) 检验。
21.2 两个人群的方差比较
21.2.1 方差比值检验
前一节介绍的样本均值比较中一个重要的前提是方差齐不齐的问题,所以本节我们就来讨论如何比较两个人群的方差是否相同,进而为均值比较时是选用方差齐的检验方法( two sample \(t\) test) 还是方差不齐的方法(Welch Two Sample \(t\) test) 提供有价值的参考信息。
比较方差是否相同,最简单的是利用 \(F\) 检验,也就是标题的方差比值检验 variance ratio test。和大多数检验方法一样,多数情况下进行的也是双侧检验,零假设是方差齐,替代假设是方差不齐。
同前例,我们用\(Y_{1i} (i=1,2,\cdots, n_1), Y_{2i} (i=1,2,\cdots,n_2)\) 标记两组从两个不同人群中随机观察的独立样本数据。两个数据服从正态分布。检验统计量是两个方差之比 \(F=\frac{\hat\sigma_1^2}{\hat\sigma_2^2}\)。这个比值距离零假设条件下的 1 越远,证明两个方差不相同的证据越强。
此时需要有 \(F\) 分布的知识,具体的推导和证明需要参考统计推断部分 (Section ??),此处直接使用其结论。如果两个独立变量,各自服从相应自由度的卡方分布,那么他们各自除以自由度后的商,服从 \(F\) 分布。正式的数学定义描述如下:
\[ \begin{aligned} & \text{If } A\sim \chi_a^2 \text{ and } B \sim \chi_b^2 \text{ independently} \\ & \text{then } F = \frac{A/a}{B/b} \sim F_{a,b} \end{aligned} \]
在应用方差比值检验时,零假设条件下(方差相等),两方差自由度分别是\(n_1-1, n_2-1\),故\(F=\frac{\hat\sigma_1^2}{\hat\ sigma_2^2} \sim F_{n_1-1, n_2-1}\),即服从自由度为\(n_1-1, n_2-1\) 的\(F\) 分布。所以需要比较计算所得的统计量 \(F\) 值的大小和相应自由度的 \(F\) 分布。
比较方差大小时,习惯上先计算两样本的方差,然后把较大的那个当作分子除以较小的那个,由此计算的检验统计量就会总是大于 \(1\)。此时我们查阅统计表格获得的 \(p\) 值是单侧的,你可以将之乘以 \(2\),或者计算另一半 \(p\) 值相加即可。 \(F\) 检验高度依赖数据服从正态分布这一前提。在R 里面var.test() 是进行\(F\) 检验的代码,另外包car 里还有leveneTest() 是一种更加稳健的比较方差的方法,适用于数据不服从正态分布时:
##
## F test to compare two variances
##
## data: Walk$Age by Walk$Group
## F = 2.2635, num df = 5, denom df = 4, p-value = 0.4488
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.2417129 16.7225792
## sample estimates:
## ratio of variances
## 2.263514## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 0.0044 0.9486
## 921.2.2 置信区间
类比章节 18.6,可以容易地推导出方差比值 \(\frac{\sigma_1^2}{\sigma_2^2}\) 的 \(95\%\) 置信区间公式为:
\[ \begin{equation} (\frac{F}{F_{n_1-1,n_2-1, 0.975}} , \frac{F}{F_{n_1-1,n_2-1,0.025}}) \end{equation} \tag{21.6} \]
上面的式子会需要计算检验统计量 \(F\) 值左侧的 \(p\) 值,一般的检验统计表个不提供。但是利用\(F\) 分布的性质如果\(F\sim F_{a,b}\) 那么\(\frac{1}{F} \sim F_{b,a}\) ,所以下面的公式在查阅表格时更加实用:
\[ (\frac{F}{F_{n_1-1,n_2-1, 0.975}} , F\times F_{n_2-1,n_1-1,0.975}) \]
21.3 比较两个百分比
21.3.1 两个百分比差是否为零的推断 Risk difference
令 \(R_1, R_2\) 为两种不同实验的成功次数,每种实验进行的次数分别是 \(n_1, n_2\)。类似地,令 \(P_1, P_2\) 表示两种实验的观察胜率。所以 \(R_1, R_2\) 服从二项分布:\(R_k \sim \text{Bin}(n_k, \pi_k) \text{ for } k=1,2\)。所以有:
\[ \begin{aligned} & E(P_k) = \pi_k \text{ and Var}(P_k) = \frac{\pi_k(1-\pi_k)}{n_k} \\ & \text{For } k = 1,2 \text{ and } P_1, P_2 \text{ independent } \end{aligned} \]
当 \(n_k\) 足够大,每个百分比都可以根据中心极限定理用下面的正态分布来近似:
\[ P_k \sim N(\pi_k, \frac{\pi_k(1-\pi_k)}{n_k}) \text{ for } k= 1,2 \]
由于两样本是独立的,所以百分比差也是服从下面的正态分布的:
\[ \begin{equation} P_2-P_1 \sim N(\pi_2-\pi_1, \frac{\pi_1(1-\pi_1)}{n_1}+\frac{\pi_2(1-\pi_2)}{n_2}) \end{equation} \tag{21.7} \]
所以,作大样本的百分比比较时,百分比差 \(\pi_2-\pi_1\) 的 \(100(1-\alpha)\%\) 置信区间公式为:
\[ (P_2-P_1) \pm z_{1-\alpha/2}\sqrt{\frac{P_1(1-P_1)}{n_1}+\frac{P_2(1-P_2)}{n_2}} \]
进行的百分比差的假设检验为: \(\text{H}_0: \pi_2-\pi_1 = 0 \text{ v.s. H}_1: \pi_2-\pi_1 \neq 0\) 检验统计量 \(Z\) 为:
\[ \begin{aligned} & Z=\frac{P_2-P_1}{\sqrt{P(1-P)(\frac{1}{n_2}+\frac{1}{n_1})}} \sim N(0,1) \ \ & \text{Where } P=\frac{R_1+R_2}{n_1+n_2} \text{ is the marginal probability of success} \\ & p\text{-value} = 2\times(1-\Phi\{ \frac{|P_2-P_1|}{\sqrt{P(1-P)(\frac{1}{n_2}+\frac {1}{n_1})}} \}) \end{aligned} \]
21.3.2 两个百分比商是否为 1 的推断 relative risk/risk ratio
两个百分比商,在流行病学中通常使用相对危险度 (relative risk) 或者危险度比 (risk ratio) 来表示。从样本数据中获得的相对危险度比的估计为 \(RR=\frac{P_2}{P_1}\)。样本量大时,百分比近似服从正态分布,所以百分比差也近似服从正态分布,然而百分比商则不然。此时用到数据的转换,将百分比商求对数以后 \(\text{log}\frac{P_2}{P_1}\) ,得到近似正态分布的对数样本分布进而进行假设检验,计算置信区间。
下一章会着重介绍数据的转换(transformation),本章暂且先用其结论,当\(Y_k=\text{log}(P_k)\) ,其方差为\(\text{Var}(Y_k) = \frac{ 1-\pi_k}{n_k\pi_k}\),所以此方差的估计量为\(\frac{1-P_k}{R_k}\)。
由此可得 \(\text{log}\frac{\pi_2}{\pi_1}\) 的 \(95\%\) 置信区间公式为:
\[ \text{log} \frac{P_2}{P_1} \pm 1.96\times\sqrt{\frac{1-P_1}{R_1}+\frac{1-P_2}{R_2}} \]
如果把上面式子计算的\(\text{log}\frac{\pi_2}{\pi_1}\) 的\(95\%\) 置信区间标记为\((L,U)\),那么相对危险度\(\frac{\ pi_2}{\pi_1}\) 的\(95\%\) 置信区间为\((exp(L), exp(U))\)。