第 35 章 二项分布数据的广义线性回归模型

二项分布数据在医学研究中很常见，例子有千千万，下面这些只是作为抛砖引玉：

  1. 心脏搭桥手术和血管成形术两组病人比较疗效时，结果变量可以是：死亡 (是/否)；心肌梗死发作 (是/否)；
  2. 机械心脏瓣膜手术结果：成功/失败；
  3. 用小鼠作不同剂量二硫化碳暴露下的毒理学实验，结果变量是：小鼠死亡 (是/否)；
  4. 队列研究中追踪对象中出现心肌梗死病例，结果变量是：心肌梗死发作 (是/否)。

35.1 汇总后/个人 (grouped / individual) 的二项分布数据

下面的数据，来自某个毒理学实验，不同剂量的二硫化碳暴露下小鼠的死亡数和总数的数据：

##    dose n_deaths n_subjects
## 1 49.06        6         59
## 2 52.99       13         60
## 3 56.91       18         62
## 4 60.84       28         56
## 5 64.76       52         63
## 6 68.69       53         59
## 7 72.61       60         62
## 8 76.54       59         60

很容易理解这是一个典型的汇总后二项分布数据 (grouped binary data)。每组不同的剂量，第二列，第三列分别是死亡数和实验总数。另外一种个人二项分布数据 (individual binary data) 的形式是这样的：

##     dose death
## 1  49.06     1
## 2  49.06     1
## 3  49.06     1
## 4  49.06     1
## 5  49.06     1
## 6  49.06     1
## 7  49.06     0
## 8  49.06     0
## 9  49.06     0
## 10 49.06     0
## 11     .     .
## 12     .     .
## 13     .     .

个人二项分布数据其实就是把每个观察对象的事件发生与否的信息都呈现出来。通常个人二项分布数据又被称为伯努利数据，分组型的二项分布数据被称为二项数据。两种表达形式，但是存储的是一样的数据。

35.2 二项分布数据的广义线性回归模型

而所有的 GLM 一样，二项分布的 GLM 包括三个部分：

  1. 因变量的分布Distribution：因变量应相互独立，且服从二项分布
    \[\begin{aligned} Y_i &\sim \text{Bin}(n_i, \pi_i), i = 1, \ cdots, n \\ E(Y_i) &= \mu_i = n_i\pi_i\end{aligned}\]
  2. 线性预测方程Linear predictor：第\(i\) 名观测对象的预测变量的线性回归模型
    $\(\eta_i = \alpha + \beta_1 x_{i1} + \cdots + \beta_p x_{ip}\) $
  3. 链接方程 Link function：链接方程连接的是 \(\mu_i = n\pi_i\) 和线性预测方程。一个二项分布因变量数据，可以有许多种链接方程：
  • \(\mathbf{logit}:\) \[\text{logit}(\pi) = \text{ln}(\frac{\pi}{1-\pi})\]
  • \(\mathbf{probit}:\) \[\text{probit}(\pi) = \Phi^{-1}(\pi)\]
  • \(\mathbf{complementary\; log-log}:\) \[\text{cloglog}(\pi) = \text{ln}\{ - \text{ln}(1-\pi) \}\]
  • \(\mathbf{log:}\) \[\text{log}(\pi) = \text{ln}(\pi)\]

注:

  1. 概率链接方程\(\text{probit}\)，\(\Phi\) 被定义为标准正态分布的累积概率方程(Section 7.3)： \[\Phi(z) = \text{Pr }(Z \leqslant z), \text{ for } Z\sim N(0,1)\]
  2. 二项分布数据的标准参数 (canonical parameter) \(\theta_i\) 的标准链接方程是 \(\theta_i = \text{logit}(\pi_i)\)。
  3. \(\text{logit, probit, complementary log-log}\) 三种链接方程都能达到把阈值仅限于\(0 \sim 1\) 之间的因变量概率映射到线性预测方程的全实数阈值\((-\ infty,+\infty)\) 的目的。但是最后一个 \(\text{log}\) 链接方程只能映射全部的非零负实数 \((-\infty,0)\)。
  4. \(\text{logit, probit}\) 链接方程都是以 \(\pi= 0.5\) 为对称轴左右对称的。但是 \(\text{cloglog}\) 则没有对称的性质。
  5. 链接方程 \(\text{log}\) 具有可以直接被解读为对数危险度比 (log Risk Ratio) 的优点，所以也常常在应用中见到。对数链接方程还有其他的优点 (非塌陷性 non-collapsibility)，但是它的最大缺点是，有时候利用这个链接方程的模型无法收敛 (converge)。
  6. \(\text{logit}\) 链接方程是我们最常见的，也最直观易于理解。利用这个链接方程拟合的模型的回归系数能够直接被理解为对数比值比 (log Odds Ratio)。
  7. 如果是个人数据 (individual data)，那么 \(n_i = 1\)，\(i\) 是每一个观测对象的编码。那么 \(Y_i = 0\text{ or }1\)，代表事件发生或没发生/成功或者失败。如果是分组数据(grouped data)，\(i\) 是每个组的编号，\(n_i\) 指的是第\(i\) 组中观测对象的人数，\(Y_i\) 是第\(i\) 组的\(n\) 名对象中事件发生的次数/成功的次数。

35.3 逻辑回归模型回归系数的实际意义

逻辑回归 (logistic regression) 的模型可以写成是

\[ \text{logist}(\pi_i) = \text{ln}(\frac{\pi_i}{1-\pi_i}) = \alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} \]

假如观察对象 \(j\) 和 \(i\) 两人中，其余的预测变量都相同，二者之间有且仅有最后一个预测变量相差一个单位：

\[ \begin{aligned} \text{logit}(\pi_j) & = \text{ln}(\frac{\pi_j}{1-\pi_j}) = \alpha + \beta_1 x_{j1} + \beta_2 x_{j2} + \cdots + \beta_p x_{jp} \\ \text{logit}(\pi_i) & = \text{ln}(\frac{\pi_i}{1-\pi_i}) = \alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} \\ \text{Because they are} & \text{ in the same model share the same parameters, and } \\ x_{jp} & = x_{ip} + 1\\ \Rightarrow \text{logit}(\pi_j) - \text{logit}(\pi_i) & = \beta_p (x_{jp} + 1 - x_{jp}) = \beta_p \\ \Rightarrow \beta_p & = \text{ln}(\frac{\pi_j}{1-\pi_j}) - \text{ln}(\frac{\pi_i}{1-\pi_i}) \\& = \text{ln}(\frac{\frac{\pi_j}{1-\pi_j}}{\frac{\pi_i}{1-\pi_i}}) \\ & = \text{ln}(\text{Odds Ratio}) \end{aligned} \]

所以回归系数 \(\beta_p\) 可以被理解为是 \(j\) 与 \(i\) 相比较时的对数比值比 log Odds Ratio。我们只要对回归系数求反函数，即可求得比值比。

35.4 逻辑回归实际案例

一组数据如下：

其中，牲畜来自两大群(group)；每群有五个组的牲畜被饲养五种不同浓度的饲料(dfactor)；每组牲畜我们记录了牲畜的总数(cattle) 以及感染了疯牛病的牲畜数量(infect)：

##    group dfactor cattle infect
## 1      1       1     11      8
## 2      1       2     10      7
## 3      1       3     12      5
## 4      1       4     11      3
## 5      1       5     12      2
## 6      2       1     10     10
## 7      2       2     10      9
## 8      2       3     12      8
## 9      2       4     11      6
## 10     2       5     10      4

35.4.1 分析目的

通过对本数据的分析，回答如下的问题：

  1. 考虑了牲畜来自两群以后，不同的饲料 (dfactor) 是否和感染疯牛病有关？
  2. 两群牲畜之间，饲料和疯牛病感染之间的关系是否不同？

35.4.2 模型1: 饲料 + 群

\[ \begin{aligned} \text{Assume } Y_i & \sim \text{Bin} (n_i, \pi_i) \\ \text{logit}(\pi_i) & = \alpha + \beta_1 x_{i1} + \beta_2 x_{i2} \end{aligned} \]

Model1 <- glm(cbind(infect, cattle - infect) ~ factor(group) + dfactor, family = binomial(link = logit), data = Cattle)
summary(Model1)
## 
## Call:
## glm(formula = cbind(infect, cattle - infect) ~ factor(group) + 
##     dfactor, family = binomial(link = logit), data = Cattle)
## 
## Coefficients:
##                Estimate Std. Error z value Pr(>|z|)    
## (Intercept)      2.1310     0.6113   3.486  0.00049 ***
## factor(group)2   1.3059     0.4654   2.806  0.00502 ** 
## dfactor         -0.7874     0.1813  -4.342 1.41e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 33.5256  on 9  degrees of freedom
## Residual deviance:  2.4508  on 7  degrees of freedom
## AIC: 32.254
## 
## Number of Fisher Scoring iterations: 4
epiDisplay::logistic.display(Model1)
##  
##                       OR lower95ci upper95ci     Pr(>|Z|)
## factor(group)2 3.6910211 1.4825101 9.1895745 5.016342e-03
## dfactor        0.4550072 0.3188999 0.6492055 1.410928e-05

于是，我们可以写下这个逻辑回归的数学模型：

\[ \begin{aligned} \text{logit}(\hat\pi_i) & = \text{ln}(\frac{\hat\pi_i}{1-\hat\pi_i}) = \hat\alpha + \hat\beta_1 x_{i1} + \hat\beta_2 x_{i2} \\ & = 2.1310 - 0.7874 \times \text{dfactor} + 1.3059 \times \text{group} \end{aligned} \]

解读这些参数估计的意义

  • 截距\(\hat\alpha = 2.1310\) 的含义是，当\(x_{1}, x_{2}\) 都等于零，i.e. 饲料浓度0，在第一群的那些牲畜感染疯牛病的对数比值( log-odds)；
  • 斜率\(\hat\beta_1 = -0.7874\) 的含义是，当牲畜群不变时，饲料浓度每增加一个单位，牲畜感染疯牛病的对数比值的估计变化量(estimated increase in log odds of infection) ；
  • 回归系数\(\hat\beta_2 = 1.3059\) 的含义是，当饲料浓度不变时，两群牲畜之间感染疯牛病的对数比值比(log-Odds Ratio)，所以第二群牲畜比第一群牲畜感染疯牛病的比值比的估计量，以及\(95\%\text{CI}\) 的计算方法就是：
    \[\begin{aligned} \text{exp}(\hat\beta_2) & = \text{exp}(1.3059) = 3.69,\\ \text{ with 95% CI: } & \text{exp}(\hat\beta_2 \pm 1.96\times \text{Std.Error}_{\hat \beta_2}) \\ & = (1.48, 9.19) \end{aligned}\]

35.4.3 模型2: 增加交互作用项 饲料 \(\times\) 群

饲料浓度与疯牛病感染之间的关系，是否因为牲畜所在的 “群” 不同而发生改变？

定义增加了饲料和群交互作用项的逻辑回归模型：

\[ \text{logit}(\pi_i) = \alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \beta_3 x_{i1}\times x_{i2} \]

Model2 <- glm(cbind(infect, cattle - infect) ~ factor(group) + dfactor + factor(group)*dfactor, family = binomial(link = logit), data = Cattle)
summary(Model2)
## 
## Call:
## glm(formula = cbind(infect, cattle - infect) ~ factor(group) + 
##     dfactor + factor(group) * dfactor, family = binomial(link = logit), 
##     data = Cattle)
## 
## Coefficients:
##                        Estimate Std. Error z value Pr(>|z|)   
## (Intercept)              1.8903     0.7358   2.569  0.01020 * 
## factor(group)2           1.9887     1.3447   1.479  0.13917   
## dfactor                 -0.7051     0.2295  -3.072  0.00213 **
## factor(group)2:dfactor  -0.2058     0.3755  -0.548  0.58362   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 33.5256  on 9  degrees of freedom
## Residual deviance:  2.1448  on 6  degrees of freedom
## AIC: 33.948
## 
## Number of Fisher Scoring iterations: 4
epiDisplay::logistic.display(Model2)
##  
##                               OR lower95ci   upper95ci    Pr(>|Z|)
## factor(group)2         7.3058042 0.5236576 101.9268681 0.139172004
## dfactor                0.4940676 0.3150615   0.7747782 0.002128977
## factor(group)2:dfactor 0.8139689 0.3898988   1.6992751 0.583618764

从输出的报告来看，增加了交互作用项以后，在第一群牲畜中，饲料浓度每增加一个单位，感染疯牛病的比值比 (OR) 是

\[ \text{exp}(-0.7051) = 0.49 \]

在第二群牲畜中，饲料浓度每增加一个单位，感染疯牛病的比值比 (OR) 变成了

\[ \text{exp}(-0.7051 - 0.2058) = 0.40 \]

通过对 \(\hat\beta_3 = 0\) 的假设检验，就可以推断饲料浓度和感染疯牛病之间的关系是否因为不同牲畜 “群” 而不同。所以上面的报告中也已经有了交互作用项的检验结果 \(p = 0.584\)，所以，此处可以下的结论是：没有足够的证据证明交互作用存在。

35.5 GLM例3

数据来自一个毒理学实验，该实验中 8 组昆虫在不同浓度的二硫化碳下暴露四个小时，实验的目的是研究二硫化碳剂量和昆虫死亡率之间的关系。

35.5.1 昆虫的死亡率

library(tidyverse)
Insect <- read.table("../backupfiles/INSECT.RAW", header =  FALSE, sep ="", col.names = c("dose", "n_deaths", "n_subjects"))
print(Insect)
##    dose n_deaths n_subjects
## 1 49.06        6         59
## 2 52.99       13         60
## 3 56.91       18         62
## 4 60.84       28         56
## 5 64.76       52         63
## 6 68.69       53         59
## 7 72.61       60         62
## 8 76.54       59         60
  1. 计算每组实验浓度下死亡昆虫的比例
Insect <- Insect %>%
  mutate(p = n_deaths/n_subjects)
print(Insect)
##    dose n_deaths n_subjects         p
## 1 49.06        6         59 0.1016949
## 2 52.99       13         60 0.2166667
## 3 56.91       18         62 0.2903226
## 4 60.84       28         56 0.5000000
## 5 64.76       52         63 0.8253968
## 6 68.69       53         59 0.8983051
## 7 72.61       60         62 0.9677419
## 8 76.54       59         60 0.9833333
  1. 将浓度和死亡比例做散点图
library(ggplot2)
ggplot(Insect, aes(x = dose, y = p)) +
  geom_point()+
  scale_x_continuous(breaks = seq(50, 75, by = 5)) +
  scale_y_continuous(breaks = seq(0, 1, by = 0.2)) +
  theme(axis.text = element_text(size = 15),
  axis.text.x = element_text(size = 15),
  axis.text.y = element_text(size = 15)) +
  labs(x = "CS2 dose (mg/L)", y = "Proportion killed")  +
  theme(axis.title = element_text(size = 17), axis.text = element_text(size = 8),
        axis.line = element_line(colour = "black"),
    panel.border = element_blank(),
    panel.background = element_blank())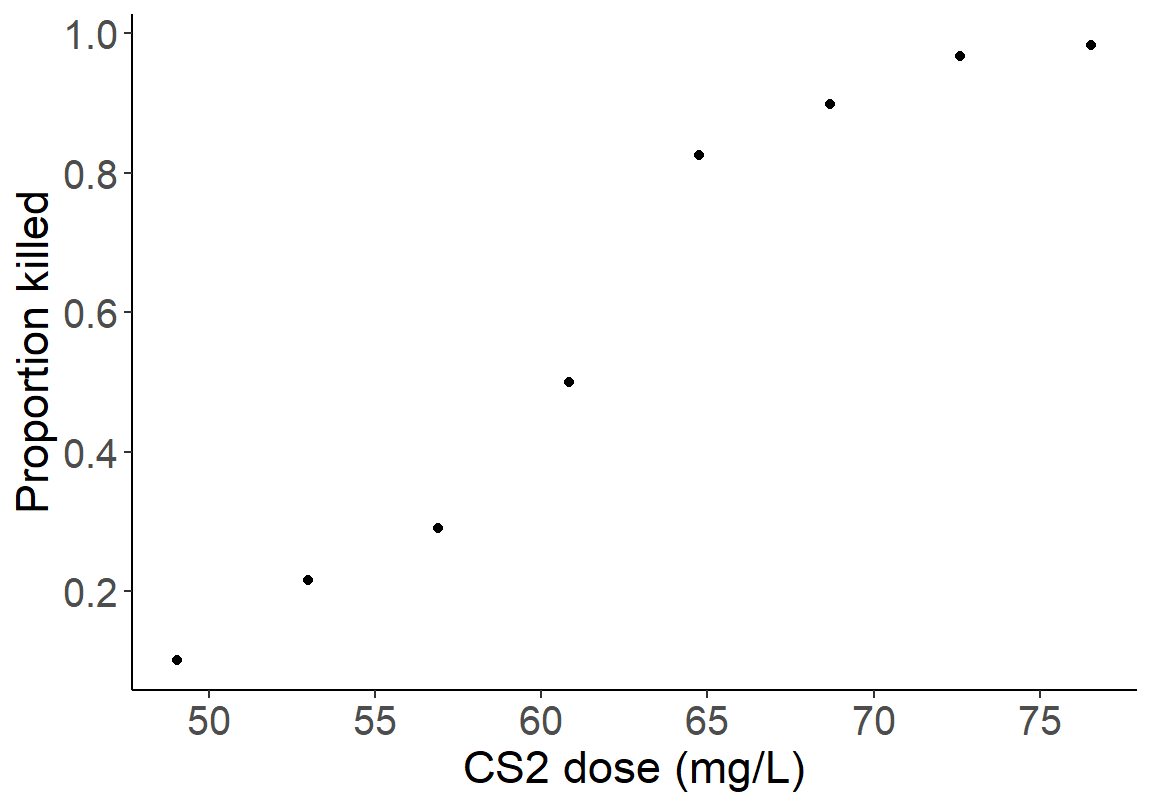
Scatter plot of CS2 dose and proportion killed.

图 35.1: Scatter plot of CS2 dose and proportion killed.

这里如果使用线性回归模型是不合适的，这是因为:

  • 散点图提示浓度和死亡比例之间不是线性关系;
  • “比例”这一数据被局限在 (0,1) 范围之内，线性回归的结果变量不会满足这个条件;
  • 观察数据本身的方差不齐，也就是每个观察点(死亡比例)的变化程度无法保证是相同的。
  1. 计算死亡比例的对数比值比 (log-odds)，再作相同的散点图，你会得出什么样的结论？
Insect <- Insect %>%
  mutate(log_odds = log(p / (1-p)))

ggplot(Insect, aes(x = dose, y = log_odds)) +
  geom_point()+
  scale_x_continuous(breaks = seq(50, 75, by = 5)) +
  scale_y_continuous(breaks = seq(-2, 4, by = 1)) +
  theme(axis.text = element_text(size = 15),
  axis.text.x = element_text(size = 15),
  axis.text.y = element_text(size = 15)) +
  labs(x = "CS2 dose (mg/L)", y = "Log odds of proportion killed")  +
  theme(axis.title = element_text(size = 17), axis.text = element_text(size = 8),
        axis.line = element_line(colour = "black"),
    panel.border = element_blank(),
    panel.background = element_blank())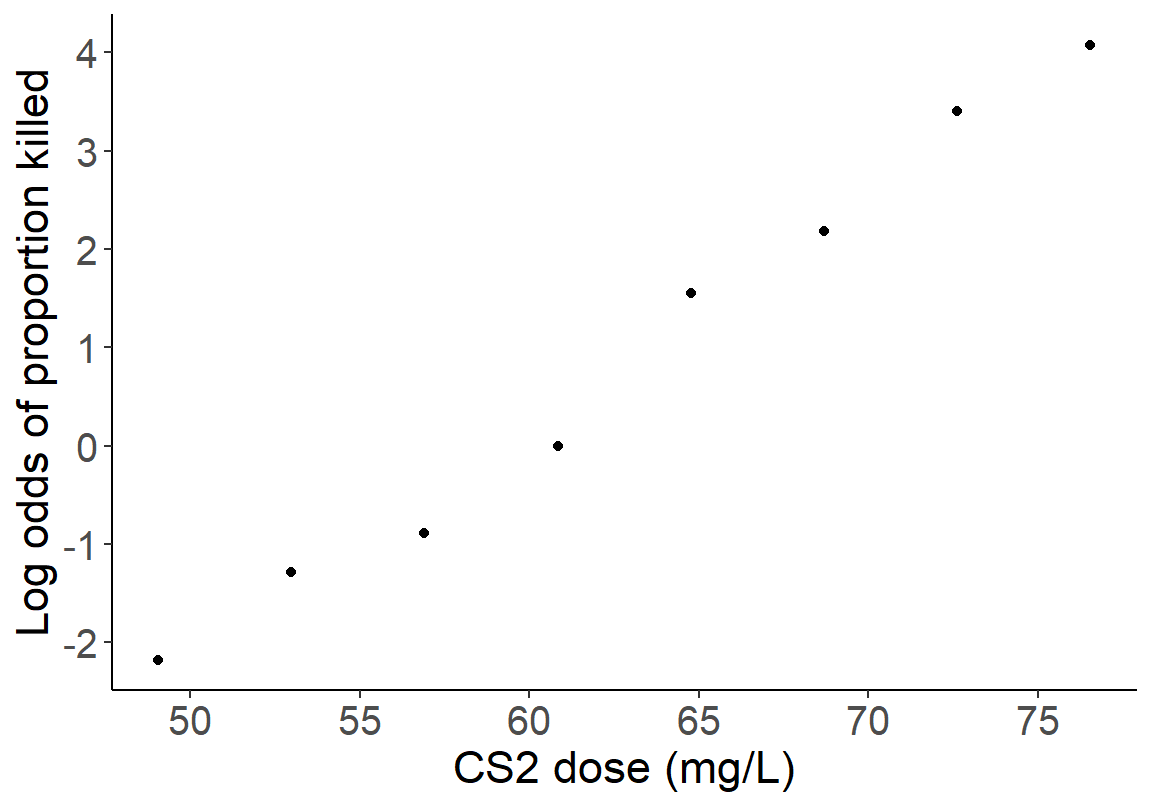
Scatter plot of CS2 dose and log-odds of proportion killed.

图 35.2: Scatter plot of CS2 dose and log-odds of proportion killed.

死亡比例的对数比值比和二硫化碳浓度之间更加接近线性关系。

  1. 写下此模型的数学表达式，你的表达式必须指明数据的分布，线性预测方程，和链接方程三个部分。用 R 拟合你写下的模型。

解

本数据中，随机变量是每组昆虫中死亡的个数。用 \(Y_i\) 标记第 \(i\) 组昆虫中死亡昆虫数量，\(d_i\) 表示第 \(i\) 组昆虫被暴露的二硫化碳浓度。对于所有的广义线性回归模型来说，它都由三个部分组成: 1) 反应量分布 the response distribution; 2) 链接方程 link function; 3) 线性预测方程 linear predictor.

反应量分布:

\[ Y_i \sim \text{Bin}(n_i, \pi_i),i = 1, \cdots, 8 \]

\(Y_i\) 的期望值是 \(\mu_i\) 的话，链接方程是

\[ \eta_i = \log(\frac{\mu_i}{n_i - \mu_i}) = \log(\frac{\pi_i}{1- \pi_i}) = \text{logit}(\pi_i) \]

线性预测方程是

\[ \eta_i = \beta_0 + \beta_1 d_i \]

用 R 来拟合这个模型:

Model1 <- glm(cbind(n_deaths, n_subjects - n_deaths) ~ dose, family = binomial(link = logit), data = Insect)
summary(Model1)
## 
## Call:
## glm(formula = cbind(n_deaths, n_subjects - n_deaths) ~ dose, 
##     family = binomial(link = logit), data = Insect)
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -14.0864     1.2284  -11.47   <2e-16 ***
## dose          0.2366     0.0203   11.65   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 268.2683  on 7  degrees of freedom
## Residual deviance:   4.6155  on 6  degrees of freedom
## AIC: 37.394
## 
## Number of Fisher Scoring iterations: 4
  1. 计算 CS2 在 55mg/l 时该模型预测的昆虫死亡概率是多少。

\[ \text{logit}(\hat\pi_i) = -14.09 + 0.2366\times55 \\ \Rightarrow \hat\pi_i = \frac{\exp(-14.09 + 0.2366\times55)}{1+\exp(-14.09 + 0.2366\times55)} = 0.254 \]

  1. 计算昆虫死亡比例达到50%的CS2浓度(LD50)。

当死亡比例达到一半时， \(\hat\pi = 0.5 \Rightarrow \text{logit}(\hat\pi) = 0\)

\[ 0 = -14.09 + 0.2366 \times \text{LD50} \\ \Rightarrow \text{LD50} = 59.5 \text{mg/l} \]

  1. 有证据证明昆虫的死亡率随着 CS2 浓度的增加而升高吗？

有极强的证据证明昆虫死亡率随着 CS2 浓度增加而升高 \((z = 11.65, P < 0.001, \text{Wald test})\)。

  1. 将参数转换成比值比，并解释其实际含义。

CS2 浓每增加1 个单位(1 mg/l)，昆虫死亡率的比值比是\(\exp(0.2366) = 1.27\)，95% 置信区间下限: \(\exp(0.2366 - 1.96\times0. 0203) = 1.22\)，上限: \(\exp(0.2366 + 1.96\times0.0203) = 1.32\)。

下面是在 R 里计算的 OR 及其对应的置信区间:

epiDisplay::logistic.display(Model1)
## 
## Logistic regression predicting cbind(n_deaths, n_subjects - n_deaths) 
##  
##                   OR(95%CI)         P(Wald's test) P(LR-test)
## dose (cont. var.) 1.27 (1.22,1.32)  < 0.001        < 0.001   
##                                                              
## Log-likelihood = -16.697
## No. of observations = 8
## AIC value = 37.394
  1. 提取模型中拟合值 fitted value
# the fitted values relate to the probability of the deaths in each group
Model1$fitted.values
##          1          2          3          4          5          6          7 
## 0.07733256 0.17518111 0.34934962 0.57637527 0.77475449 0.89707745 0.95658687 
##          8 
## 0.98240554
# to calculate the counts of numbers of deaths in each group
Model1$fitted.values * Insect$n_subjects
##         1         2         3         4         5         6         7         8 
##  4.562621 10.510866 21.659677 32.277015 48.809533 52.927570 59.308386 58.944332
  1. 把模型拟合的概率和观测概率放在同一个散点图中比较:
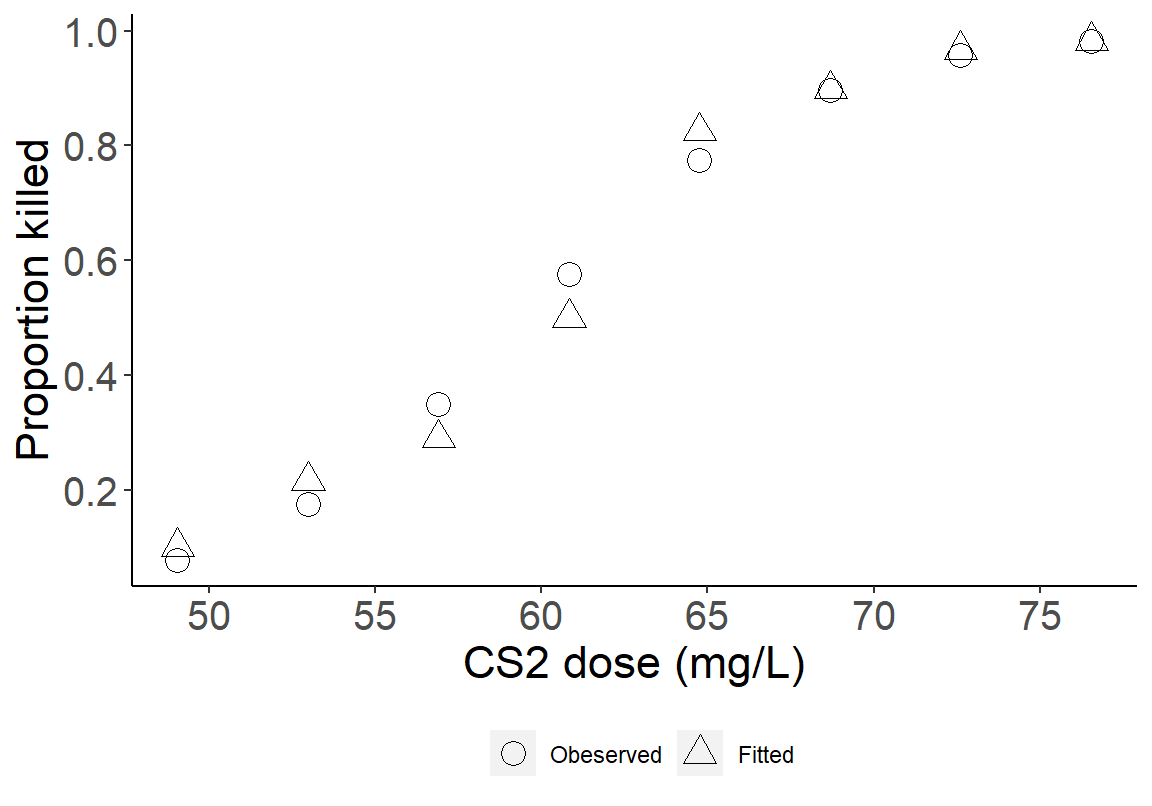
Observed (circles) and fitted (triangles) proportions are generally similar, with differences greatest in the third and fourth dose groups.

图 35.3: Observed (circles) and fitted (triangles) proportions are generally similar, with differences greatest in the third and fourth dose groups.

  1. 现在计算一个新的浓度值 dose2 = dose2。这个新的变量用于分析是否模型中使用浓度平方可以提升模型的拟合优度。 1) 用 Wald 检验的结果说明浓度平方的回归系数是否有意义。 2) 新模型的拟合值是否有所改善？
Insect <- Insect %>%
  mutate(dose2 = dose^2)
Model2 <- glm(cbind(n_deaths, n_subjects - n_deaths) ~ dose + dose2, family = binomial(link = logit), data = Insect)
summary(Model2)
## 
## Call:
## glm(formula = cbind(n_deaths, n_subjects - n_deaths) ~ dose + 
##     dose2, family = binomial(link = logit), data = Insect)
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.488172   9.867720  -0.252    0.801
## dose        -0.150005   0.329179  -0.456    0.649
## dose2        0.003187   0.002727   1.169    0.243
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 268.2683  on 7  degrees of freedom
## Residual deviance:   3.1836  on 5  degrees of freedom
## AIC: 37.962
## 
## Number of Fisher Scoring iterations: 4

加入了浓度平方以后，该项本身的 Wald 检验结果告诉我们，没有证据证明浓度和昆虫死亡比例的对数比值比之间呈抛物线关系。

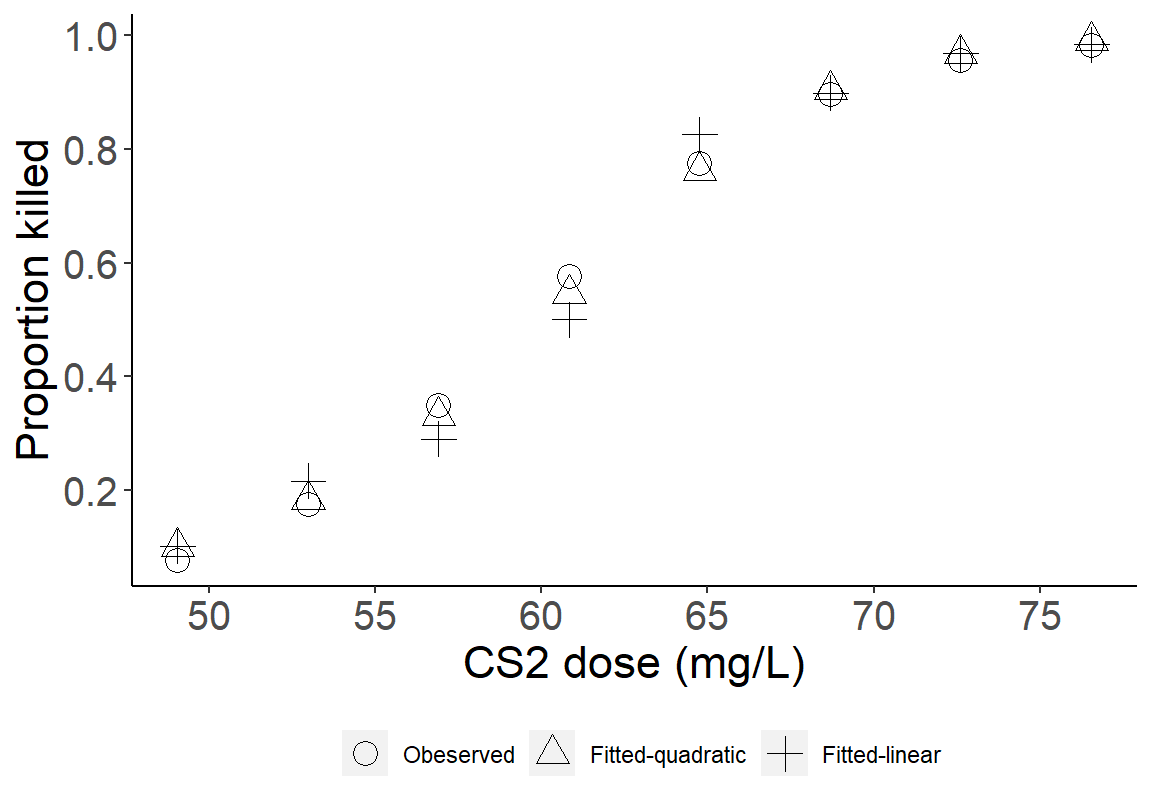
Fitted probabilities for each dose from two models

图 35.4: Fitted probabilities for each dose from two models

加入浓度平方二次项的模型在第三和第四组给出了比一次模型更加接近观测值的估计。但是这种提升是极为有限的，且统计学上加入的二次项的回归系数并无意义。

所以，本数据分析的结论是，有很强的证据证明昆虫死亡的概率随着CS2 浓度的升高而升高 (P<0.001)。死亡的比值 (odds)，随着浓度每升高1个单位 (mg/l) 而升高 27% (95% CI: 22%-32%)。

35.5.2 哮喘门诊数据

在一项横断面研究中，访问哮喘门诊连续达到 6 个月以上的全部患者被一一询问其目前的用药情况和症状。下面的表格总结的是这些患者中，目前使用口服类固醇药物与否，及患者报告夜间由于哮喘症状而从睡眠中醒来的次数。

表 35.1: Frequency of night waking due to asthma
Corticosteroids Never Less.than.once.a.week More.than.once.a.week Every.night
User 27 41 44 38
Non-user 20 10 8 22

下面的 STATA 输出报告，是对上述数据拟合的逻辑回归的结果。其中变量 user 和 never 被编码为 0/1，1 代表该患者正在使用口服类固醇药物，或者从未因为哮喘而在夜间醒来。变量 sev 是患者自己报告的哮喘症状严重程度 (0-3 分，分数越高症状越严重)。

  1. 用表格的数据实施了一个总体的卡方检验还有一个卡方检验的倾向性检验。这两个卡方检验的统计量分别是 12.87, 和 0.25。请解释这两个统计量的实际含义。
    在零假设 – 使用口服类固醇药物和夜间因为哮喘而醒来次数之间没有关系 – 条件下，表格总体的卡方检验服从 \(\chi^2_3\) 分布。查表或者在 R 里使用
1-pchisq(12.87, 3)
## [1] 0.004926341

可以知道 p = 0.005。这是极强的反对零假设的证据。 相反，卡方检验的倾向性检验结果是 p = 0.62，这个结果提示使用类固醇药物所占的比例没有倾向性:

1-pchisq(0.25, 1)
## [1] 0.6170751

两个卡方检验的显著不同应是因为用类固醇药物的患者比例在”从不”, “低于每周一次”，“多余每周一次” 中递增，但是到了最后一组”每天” 时又下降。倾向性检验比起总体的卡方检验在关系是单调递增或者单调递减时统计学效能更好，但是当关系变得复杂以后，倾向性卡方检验变得不再有优势。倾向性检验其实等同于用一个变量 (用药与否) 和另一个变量 (夜间因为哮喘醒来次数) 做线性回归。对于这个表格的数据来说，这是一个 U 型的关系，所以做线性回归的结果也是会给出没有意义的 p 值。

  1. 利用 STATA 的逻辑回归报告，能对哮喘的严重程度和患者报告夜间从未因为哮喘醒来(never wake up)之间的关系作出怎样的结论？
    从 STATA 计算的结果来看，该数据提供了极强的证据证明哮喘的严重程度和报告从未因哮喘而醒来之间呈负相关。特别地，哮喘严重程度为2 的患者比1 的患者报告从未醒来的比值比(odds ratio) 是0.077 (95% CI: 0.027, 0.224, p < 0.001); 哮喘严重程度为3 的患者比1 的患者报告醒来的比值比是0.0128 (95% CI: 0.0022, 0.0738, p < 0.001)。所以，哮喘越严重，报告夜里从未醒来的概率越低。

  2. 利用 STATA 的逻辑回归报告，能对是否使用口服类固醇药物和报告从未因哮喘而醒来之间的关系作出怎样的结论？
    如果要计算未调整的比值比，我们可以把表格中第2-4列的数据合并，那么在使用类固醇药物的患者(n = 150) 中27 人报告从未醒来，在不使用类固醇药物的患者中(n = 60)，有20 人报告从未醒来。这样未调整的比值比就是 \(\frac{27 \times 40}{20 \times 123} = 0.44\)。 STATA 计算的逻辑回归模型的结果显示，这一数字在调整了哮喘症状之后，发生了本质的变化: \(e^{0.815} = 2.26\)。虽然调整后的比值比并没有统计学意义。但是它从小于 1 变成了大于 1，方向上发生了转变。所以，调整了哮喘严重程度之后，数据似乎提示使用类固醇药物和报告从不在夜间因哮喘醒来的概率呈正相关 (用药者睡得更好)，但是这个相关性没有统计学意义，其95%置信区间很宽。

  3. 从这些分析来看，哮喘严重程度和是否口服类固醇药物之间有什么样的关系？
    因为用类固醇药物和报告夜间不曾醒来在调整了哮喘严重程度之后从原先的负相关变成了正相关。又因为哮喘严重程度本身和报告夜间不曾醒来之间是负相关，所以，是否口服类固醇药物和哮喘严重程度之间呈正相关，也就是哮喘越严重，患者越倾向于使用类固醇药物。