第 24 章 最小二乘估计的性质和推断
前一章介绍了简单线性回归模型中对总体参数\(\alpha, \beta, \sigma^2\) 的估计公式,分别是(23.5) (23.6) (23.9)。本章继续介绍他们的统计学性质。下面的标记和统计量也会被用到:
- \(\bar{y}=\frac{\sum_{i=1}^n y_i}{n}\),因变量 \(y\) 的样本均值;
- \(\bar{x}=\frac{\sum_{i=1}^n x_i}{n}\),预测变量 \(x\) 的样本均值;
- \(SS_{yy}=\sum_{i=1}^n(y_i-\bar{y})^2\),因变量 \(y\) 的校正平方和;
- \(SS_{xx}=\sum_{i=1}^n(x_i-\bar{x})^2\),预测变量 \(x\) 的校正平方和;
- \(SD_y^2=\frac{\sum_{i=1}(y_i-\bar{y})^2}{n-1}=\frac{SS_{yy}}{n-1}\),因变量\(y\) 的样本方差;
- \(SD_x^2=\frac{\sum_{i=1}(x_i-\bar{x})^2}{n-1}=\frac{SS_{xx}}{n-1}\),预测变量\(x\) 的样本方差;
- \(S_{xy}=\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})\),\(x,y\) 的交叉乘积;
- \(CV_{xy}=\frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{n-1}=\frac{S_{ xy}}{n-1}\),样本协方差;
- \(r_{xy}=\frac{CV_{xy}}{SD_xSD_y}\),\(x,y\) 的样本相关系数;
- \(SS_{RES}=\sum_{i=1}^n\hat\varepsilon^2=\sum_{i=1}^n(y_i-\hat\alpha-\hat\beta x_i)^2\) ,残差的估计平方和。
24.1 OLS 估计量的性质
- 样本估计的回归直线必定穿过数据的中心 \((\bar{x},\bar{y})\)。
证明
由于样本估计的截距和斜率公式 (23.5) (23.6) 可知:
\[ \begin{aligned} \hat\alpha &= \bar{y} - \hat\beta\bar{x} \\ \hat y_i &= \hat\alpha + \hat\beta x_i \\ \Rightarrow \hat y_i &= \bar{y}+\hat\beta(x_i-\bar{x}) \end{aligned} \tag{24.1} \]
所以,当 \(\hat x_i=\bar{x}\) 时 \(\hat y_i=\bar{y}\)。即回归直线必然穿过中心点。
- 如果拟合模型是正确无误的, \(\hat\alpha,\hat\beta,\hat\sigma^2\) 分别是各自的无偏估计。
- \(\hat\alpha, \hat\beta\) 是极大似然估计, \(\hat\sigma^2\) 不是MLE。
- \(\hat\alpha, \hat\beta\) 是 \(\alpha, \beta\) 最有效的估计量。
24.2 \(\hat\beta\) 的性质
\[ \begin{equation} \hat\beta=\frac{S_{xy}}{SS_{xx}}=\frac{CV_{xy}}{SD_x^2} \end{equation} \tag{24.2} \]
24.2.1 \(Y\) 对 \(X\) 回归, 和 \(X\) 对 \(Y\) 回归
如果我们使用 \(\hat\beta_{y|x}\) 表示预测变量 \(x\),因变量 \(y\) 的简单线性回归系数,那么我们就有:
\[ \begin{equation} \hat\beta_{y|x} = \frac{CV_{xy}}{SD_x^2} \text{ and } \hat\beta_{x|y} = \frac{CV_{xy}}{SD_y^2 } \\ \text{Hence, } \hat\beta_{y|x}\hat\beta_{x|y} = r^2_{xy} \end{equation} \tag{24.3} \]
公式(24.3) 也证明了:如果两个变量相关系数为\(1\) (100% 相关), \(Y\) 对\(X\) 回归的回归系数,是\(X\) 对\(Y\) 回归的回归系数的倒数。
24.2.2 例 1: 还是图 23.1 数据
library(haven)
growgam1 <- read_dta("../Datas/growgam1.dta")
# regress wt on age
summary(lm(wt~age, data=growgam1))##
## Call:
## lm(formula = wt ~ age, data = growgam1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.9242 -0.7849 0.0071 0.7975 4.0678
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.83758 0.21007 32.55 <2e-16 ***
## age 0.16533 0.01111 14.88 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.274 on 188 degrees of freedom
## Multiple R-squared: 0.5408, Adjusted R-squared: 0.5383
## F-statistic: 221.4 on 1 and 188 DF, p-value: < 2.2e-16## Analysis of Variance Table
##
## Response: wt
## Df Sum Sq Mean Sq F value Pr(>F)
## age 1 359.06320 359.06320 221.39203 < 2.22e-16 ***
## Residuals 188 304.90655 1.62184
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = age ~ wt, data = growgam1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -16.0099 -4.2393 0.0831 3.1299 21.1112
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -14.5680 2.1597 -6.746 1.83e-10 ***
## wt 3.2709 0.2198 14.879 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.664 on 188 degrees of freedom
## Multiple R-squared: 0.5408, Adjusted R-squared: 0.5383
## F-statistic: 221.4 on 1 and 188 DF, p-value: < 2.2e-16## Analysis of Variance Table
##
## Response: age
## Df Sum Sq Mean Sq F value Pr(>F)
## wt 1 7103.6730 7103.6730 221.39203 < 2.22e-16 ***
## Residuals 188 6032.2428 32.0864
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1可以看到二者的输出结果中统计检验量一样,但是一个是将体重针对年龄回归,另一个则是反过来,所以回归系数和截距都不同。回归方程的含义也就发生了变化。如果把两条回归曲线同时作图可以更加直观:
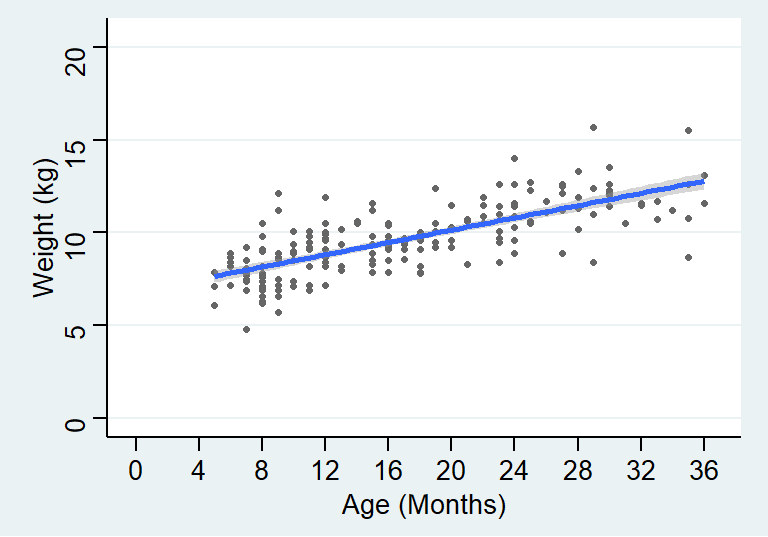
图 24.1: Simple linear regression model line relating weight to age
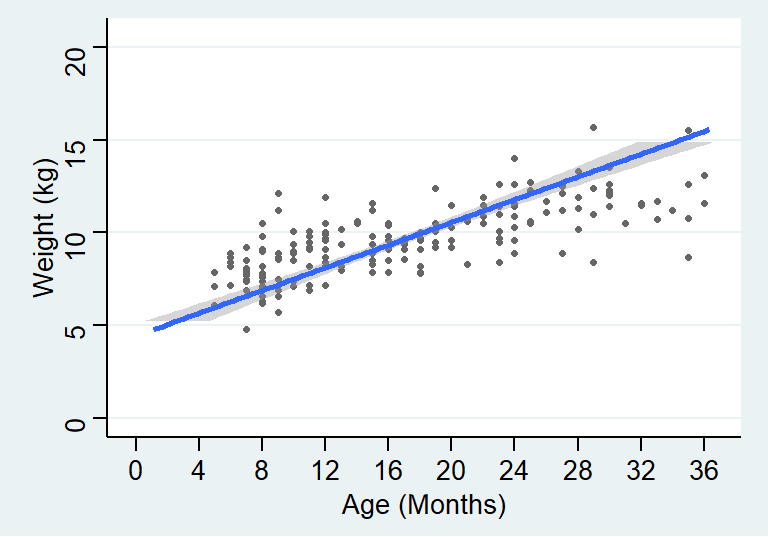
图 24.2: Simple linear regression model line relating age to weight
24.3 截距和回归系数的方差,协方差
假如简单线性回归模型是正确的,那么截距 \(\hat\alpha\) 和回归系数 \(\hat\beta\) 的方差分别是:
\[ \begin{equation} V(\hat\alpha) = \sigma^2(\frac{1}{n}+\frac{\bar{x}^2}{SS_{xx}}) = \frac{\sigma^2}{ (n-1)} (1-\frac{1}{n}+\frac{\bar{x}^2}{SD_x^2}) \end{equation} \tag{24.4} \]
\[ \begin{equation} V(\hat\beta) = \frac{\sigma^2}{SS_{xx}}=\frac{\sigma^2}{(n-1)SD_x^2} \end{equation} \tag{24.5} \]
从公式(24.4) 和(24.5) 也可以看出,两个估计量的方差随着残差方差的增加而增加(估计不精确),随着样本量的增加而减少(估计更精确)。截距 \(\hat\alpha\) 的方差会随着样本均值的增加而增加。
通常来说,截距和回归系数二者之间并非相互独立。他们的协方差为:
\[ \begin{equation} Cov(\hat\alpha,\hat\beta) = -\frac{\sigma^2\bar{x}}{SS_{xx}} \end{equation} \tag{24.6} \]
上面的公式 (24.4) (24.5) (24.6) 都包含了真实的残差方差 \(\sigma^2\)。这个量对于我们“人类”来说是未知的。
24.3.1 中心化 centring
简单线性回归模型常用的一个技巧是将预测变量中心化。即,求预测变量的均值,然后将每个观测值减去均值之后再用这个新的预测变量拟合简单线性回归模型。这样做其实完全不影响回顾系数,却会影响截距的大小。此时新的回归直线的截距,就等于因变量 (体重) 的均值。
用图 23.1 数据来解释:
## [1] 16.97895growgam1$age_cen <- growgam1$age-mean(growgam1$age)
# regress wt on age
print(summary(lm(wt~age, data=growgam1)), digit=5)##
## Call:
## lm(formula = wt ~ age, data = growgam1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.92418 -0.78489 0.00710 0.79747 4.06781
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.837584 0.210070 32.549 < 2.2e-16 ***
## age 0.165331 0.011112 14.879 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.2735 on 188 degrees of freedom
## Multiple R-squared: 0.54078, Adjusted R-squared: 0.53834
## F-statistic: 221.39 on 1 and 188 DF, p-value: < 2.22e-16##
## Call:
## lm(formula = wt ~ age_cen, data = growgam1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.92418 -0.78489 0.00710 0.79747 4.06781
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.644737 0.092391 104.391 < 2.2e-16 ***
## age_cen 0.165331 0.011112 14.879 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.2735 on 188 degrees of freedom
## Multiple R-squared: 0.54078, Adjusted R-squared: 0.53834
## F-statistic: 221.39 on 1 and 188 DF, p-value: < 2.22e-16很明显,结果显示中心化不会改变回归系数,也不会改变它的方差。但是“新”的截距,其实就等于因变量 (体重) 的均值。而且很多数据都集中在这个均值附近,因而,截距的方差比没有中心化的回归方程要小。
24.4 \(\alpha, \beta\) 的推断
\(\hat\alpha, \hat\beta\) 都可以被改写成关于因变量 \(Y\) 的方程,因此同时也是随机误差的方程式:
\[ \begin{aligned} \hat\beta &= \sum_{i=1}^n[\frac{(x_i-\bar{x})}{SS_{xx}}(y_i-\bar{y})] \\ \text{Substituting } &(y_i-\bar{y}) = \beta(x_i-\bar{x})+(\varepsilon_i-\bar{\varepsilon}) \\ &= \beta + \sum_{i=1}^n[\frac{x_i-\bar{x}}{SS_{xx}}(\varepsilon_i-\bar{\varepsilon})] \end{aligned} \]
又因为,\(\varepsilon_i \sim NID(0,\sigma^2)\),估计量\(\hat\alpha, \hat\beta\) 均为\(\varepsilon_i\) 的线性转换,所以他们也都是服从正态分布的。
24.4.1 对回归系数进行假设检验
对于回归系数 \(\beta\),我们可以使用 Wald statistic (Section 15.3) 进行零假设为 \(\text{H}_0: \beta=0\) 的假设检验。此时,替代假设为 \(\text{H}_1: \beta\neq0\)。最佳检验统计量为:
\[ \begin{equation} t = \frac{\hat\beta-0}{SE(\hat\beta)} \\ \end{equation} \tag{24.7} \]
根据公式(24.5) \(SE(\hat\beta) = \sqrt{V(\hat\beta)} = \frac{\hat\sigma}{\sqrt{SS_{xx}}}\) 。用\(\hat\sigma^2\) 替换掉公式(24.5) 中的\(\sigma^2\),意味着回归系数的检验统计量\(t\) 服从自由度为\(n-2\) 的\(t\) 分布。之后就可以根据 \(t\) 分布的性质求相应的 \(p\) 值了,对相关系数是否为 \(0\) 进行检验。之所以我们可以在这里使用Wald 检验,是因为前提条件:随机误差服从正态分布,于是\(\beta\) 的对数似然比也是左右对称的,当对数似然比的图形左右对称时,就可以使用二次方程来近似(Wald 检验的实质)。
24.4.2 回归系数,截距的置信区间
估计量 \(\beta\) 的 \(95\%\) 置信区间的计算公式如下:
\[ \begin{equation} \hat\beta \pm t_{n-2,0.975}SE(\hat\beta) \end{equation} \tag{24.8} \]
其中,\(t_{n-2, 0.975}\) 表示自由度为 \(n-2\) 的 \(t\) 分布的 \(97.5\%\) 位点的值。继续使用之前的实例,图 23.1 中的数据。体重对年龄进行简单线性回归之后,年龄的估计回顾系数\(\hat\beta=0.165, SE(\hat\beta)=0.0111\), 此例中\(n=190\),所以\(t_{188, 0.975} =1.973\)。所以回归系数的 \(95\%\) 置信区间可以如此计算:\(0.165\pm1.973\times0.0111=(0.143, 0.187)\)。
类似的,估计截距 \(\hat\alpha\) 的 \(95\%\) 置信区间的计算式便是: \(\hat\alpha \pm t_{n-2, 0.975}SE(\hat\alpha)\)。同样的例子里,\(\hat\alpha=6.838, SE(\hat\beta) = 0.210, t_{188, 0.975}=1.973\)。所以截距的 \(95\%\) 置信区间的计算方法就是: \(6.838\pm1.973\times0.210=(6.42, 7.25)\)
跟下面 R 计算的完全一样:
## 2.5 % 97.5 %
## (Intercept) 6.4231866 7.2519817
## age 0.1434121 0.187250724.4.3 预测值的置信区间 (置信带) - 测量回归曲线本身的不确定性
这里所谓的“预测值”其实并没有拿来预测什么新的数值,而是说我们希望通过线性回归找到因变量真实值的存在区间 (置信区间)。所以这个预测值的真实含义其实应该是在预测变量取 \(X=x\) 时,因变量的期待值,\(E(Y|X=x)\)。
这个预测值的方差公式如下:
\[ \begin{equation} V(\hat y_{x}) = \sigma^2[\frac{1}{n}+\frac{(x_i-\bar{x})^2}{SS_{xx}}] \end{equation} \tag{24.9} \]
于是可以计算它的 \(95\%\) 置信区间公式是:
\[ \begin{equation} \hat y_x \pm t_{n-2, 0.975} \hat\sigma \sqrt{[\frac{1}{n}+\frac{(x-\bar{x})^2}{SS_{xx} }]} \end{equation} \tag{24.10} \]
其实在之前的图 (图 23.2) 我们也已经展示过这个置信区间的范围。
24.4.4 预测带 Reference range - 包含了 95% 观察值的区间
此处的 \(95\%\) 预测带,其实是包含了 \(95\%\) 观察数据的区间。所以预测带要比置信带更宽。它的方差计算公式为:
\[ \begin{equation} V(\hat y_x)+\sigma^2 = \sigma^2[1+\frac{1}{n}+\frac{(x-\bar{x})^2}{SS_{xx}}] \end{equation} \tag{24.11} \]
区间计算公式为:
\[ \begin{equation} \hat{y}_x \pm t_{n-2, 0.975} \sqrt{1+\frac{1}{n}+\frac{(x-\bar{x})^2}{SS_{xx} }} \end{equation} \tag{24.12} \]
将置信带和预测带同时展现则如下图:
growgam1 <- read_dta("../Datas/growgam1.dta")
Model <- lm(wt~age, data=growgam1)
temp_var <- predict(Model, interval="prediction")
new_df <- cbind(growgam1, temp_var)
ggplot(new_df, aes(x=age, y=wt)) + geom_point(shape=20, colour="grey40") +
stat_smooth(method = lm, se=TRUE, size = 0.3) +
geom_line(aes(y=lwr), color = "red", linetype = "dashed")+
geom_line(aes(y=upr), color = "red", linetype = "dashed")+
scale_x_continuous(breaks=seq(0, 38, 4),limits = c(0,36.5))+
scale_y_continuous(breaks = seq(0, 20, 5),limits = c(0,20.5)) +
theme_stata() +labs(x = "Age (Months)", y = "Weight (kg)")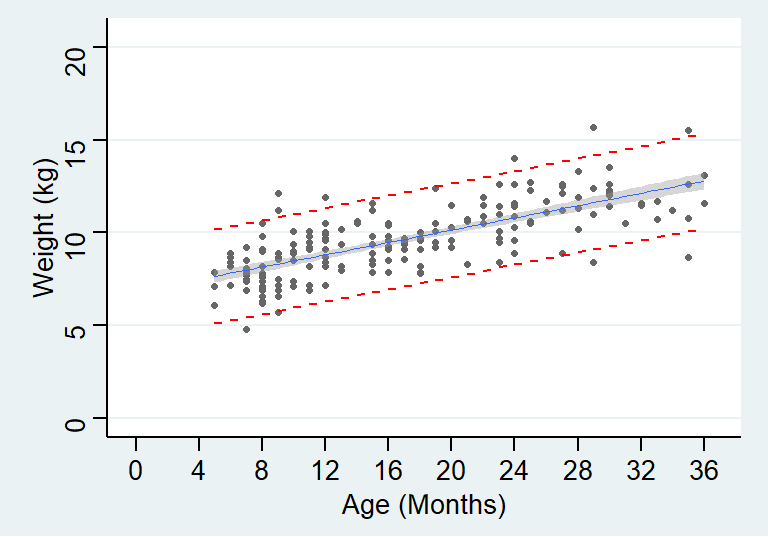
图 24.3: Simple linear regression for age and weight of children in a cross-sectional survey with 95% CI of predicted values and 95% reference range
24.5 线性回归模型和 Pearson 相关系数
前面也推导过线性回归系数和 Pearson 相关系数之间的关系 (Section 24.2.1),这里详细再展开讨论它们之间关系的另外两个重要结论。
24.5.1 \(r^2\) 可以理解为因变量平方和被模型解释的比例
Pearson 相关系数,因变量的平方和,模型的残差平方和之间有如下的关系:
\[ \begin{equation} r^2 = \frac{SS_{yy}-SS_{RES}}{SS_{yy}} = 1-\frac{SS_{RES}}{SS_{yy}} \end{equation} \tag{24.13} \]
证明
\[ \frac{SS_{RES}}{SS_{yy}} = \frac{\sum_{i=1}^n(y_i-\hat\alpha-\hat\beta x_i)^2}{\sum_{i= 1}^n(y_i-\bar{y})^2} \]
因为 (23.5) : \(\hat\alpha=\bar{y}-\hat{\beta}\bar{x}\)
\[ \begin{aligned} \frac{SS_{RES}}{SS_{yy}} &= \frac{\sum_{i=1}^n[(y_i-\bar{y})-\hat\beta(x_i-\bar{x })]^2}{\sum_{i=1}^n(y_i-\bar{y})^2} \\ &=\frac{\sum_{i=1}^n(y_i-\bar{y})^2}{\sum_{i=1}^n(y_i-\bar{y})^2}-\ frac{2\hat\beta\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n(y_i-\bar {y})^2}+\frac{\hat\beta^2\sum_{i=1}^n(x_i-\bar{x})^2}{\sum_{i=1}^n(y_i -\bar{y})^2}\\ &=1-\frac{2\hat\beta S_{xy}}{SS_{yy}} + \frac{\hat\beta^2SS_{xx}}{SS_{yy}} \end{aligned} \]
又因为\(\hat\beta=\frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n( x_i-\bar{x})^2}=\frac{S_{xy}}{SS_{xx}}, r^2=\frac{S_{xy}^2}{SS_{xx}SS_{yy} }\)。
\[ \begin{aligned} \frac{SS_{RES}}{SS_{yy}} &= 1-\frac{2S_{xy}^2}{SS_{yy}SS_{xx}}+\frac{S_{xy}^2}{ SS_{xx}SS_{yy}}\\ &=1-2r^2+r^2\\ &=1-r^2\\ \Rightarrow r^2&=1-\frac{SS_{RES}}{SS_{yy}} \end{aligned} \]
因此,这里就引出了非常重要的一个结论,Pearson 相关系数的平方\(r^2\) 的统计学含义是,因变量的平方和\(SS_{yy}\) 中,模型的预测变量能够解释的部分\(1-SS_{RES}\) 的百分比。 统计学结果的报告中,为了和一般相关系数的意义区分,会用大写的 \(R^2\) 来表示这个模型解释了因变量的百分比。 (Section 25.2.3)
24.6 Pearson 相关系数和模型回归系数的检验统计量 \(t\) 之间的关系
\[ \begin{equation} t=r\sqrt{\frac{n-2}{1-r^2}} \end{equation} \tag{24.14} \]
证明
由于前面推导的 \(r^2\) 公式 (24.13),而且 \(r^2=\frac{S_{xy}^2}{SS_{xx}SS_{yy}}\):
\[ \begin{aligned} \frac{r^2}{1-r^2} & = \frac{\frac{S_{xy}^2}{SS_{xx}SS_{yy}}}{\frac{SS_{RES}}{ SS_{yy}}} \\ & = \frac{S_{xy}^2}{SS_{xx}SS_{RES}} \\ & = \frac{S_{xy}^2}{SS_{xx}(n-2)\hat\sigma^2} \end{aligned} \]
由于公式 (24.5),所以 \(\hat\sigma^2=V(\hat\beta)SS_{xx}\)
\[ \begin{aligned} \frac{r^2}{1-r^2} & = \frac{S_{xy}^2}{SS^2_{xx}(n-2)V(\hat\beta)} \\ & = \frac{\hat\beta^2}{(n-2)V(\hat\beta)} \\ \Rightarrow t=r\sqrt{\frac{n-2}{1-r^2}} \end{aligned} \]
这个结论也被用于相关系数的假设检验。而且也正如 Section 24.2.1 证明过的那样,在简单线性回归里因变量和预测变量的位置对调以后,对于回顾系数是否为零的检验统计量不受影响。
24.7 实例
数据同前一章练习部分数据相同 23.8:
# 数据读入
Chol <- read_dta("../Datas/chol.dta")
Model <- lm(chol2~chol1, data=Chol)
print(summary(Model), digit=6)##
## Call:
## lm(formula = chol2 ~ chol1, data = Chol)
##
## Residuals:
## Min 1Q Median 3Q Max
## -56.87654 -22.06181 1.84937 16.63107 84.11839
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 110.4246582 20.0113279 5.51811 2.8499e-07 ***
## chol1 0.5786806 0.0747598 7.74053 9.5114e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 30.163 on 97 degrees of freedom
## Multiple R-squared: 0.381834, Adjusted R-squared: 0.375462
## F-statistic: 59.9159 on 1 and 97 DF, p-value: 9.51139e-12## Analysis of Variance Table
##
## Response: chol2
## Df Sum Sq Mean Sq F value Pr(>F)
## chol1 1 54511.7 54511.7 59.9159 9.5114e-12 ***
## Residuals 97 88250.9 909.8
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# 计算截距和回归系数的 P 值 HAND CALCULATIONS twosided p-value in R can be obtained by pt(t, df) function
## p value for intercept:
110.42466/20.01133 #=5.518107## [1] 5.518107## [1] 2.849884e-07## [1] 7.740503## [1] 9.512857e-12# add fitted regression lines 95% CIs and reference range
temp_var <- predict(Model, interval="prediction")
new_df <- cbind(Chol, temp_var)
ggplot(new_df, aes(x=chol1, y=chol2)) + geom_point(shape=20, colour="grey40") +
stat_smooth(method = lm, se=TRUE, size=0.5) +
geom_line(aes(y=lwr), color = "red", linetype = "dashed")+
geom_line(aes(y=upr), color = "red", linetype = "dashed")+
scale_x_continuous(breaks=seq(150, 400, 50),limits = c(150, 355))+
scale_y_continuous(breaks=seq(150, 400, 50),limits = c(150, 355)) +
theme_stata() +labs(x = "Cholesterol at visit 1 (mg/100ml)", y = "Cholesterol at visit 2 (mg/100ml)")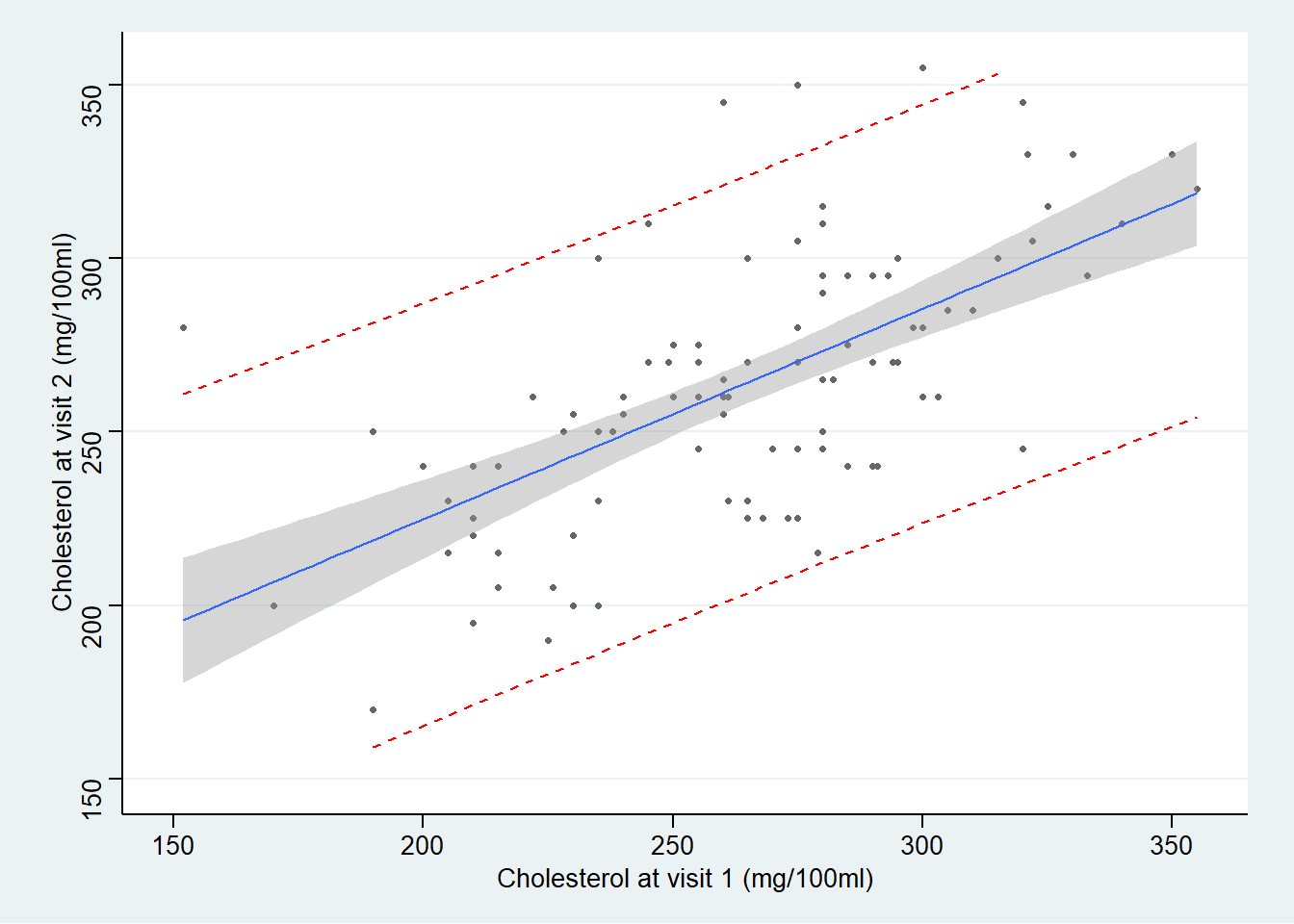
图中可见,95% 置信带变化显著,距离均值越远的地方,置信带越宽。然而预测带基本是平行的没有变化。因为预测带的涵义是,95%的观察数据都在这个区间范围内。