第 8 章 中心极限定理

8.1 协方差

两个独立连续随机变量 \(X,Y\) 之和的方差 Variance有 ：

\[\text{Var}(X+Y)=\text{Var}(X)+\text{Var}(Y)\]

然而如果他们并不相互独立的话：

\[ \begin{aligned} \text{Var}(X+Y) &= E[((X+Y)-E(X+Y))^2] \\ &= E[(X+Y)-(E(X)+E(Y))^2] \\ &= E[(X-E(X)) - (Y-E(Y))^2] \\ &= E[(X-E(X))^2+(Y-E(Y))^2 \\ & \;\;\; +2(X-E(X))(Y-E(Y))] \\ &= \text{Var}(X)+\text{Var}(Y)+2E[(X-E(X))(Y-E(Y))] \end{aligned} \]

可以发现在两者和的方差公式展开之后多了一部分 \(E[(X-E(X))(Y-E(Y))]\)。这个多出来的一部分就说明了二者 \((X, Y)\) 之间的关系。它被定义为协方差 (Covariance): \[\text{Cov}(X,Y) = E[(X-E(X))(Y-E(Y))]\]

所以：

\[\text{Var}(X+Y)=\text{Var}(X)+\text{Var}(Y)+2Cov(X,Y)\]

要记住，协方差只能用于评价\(X,Y\)之间的线性关系 (Linear Association)。

以下是协方差 (Covariance) 的一些特殊性质：

  1. \(\text{Cov}(X,X)=\text{Var}(X)\)
  2. \(\text{Cov}(X,Y)=\text{Cov}(Y,X)\)
  3. \(\text{Cov}(aX,bY)=ab\:\text{Cov}(X,Y)\)
  4. \[\text{Cov}(aR+bS,cX+dY)=ac\:\text{Cov}(R,X)+ad\:\text{Cov}(R,Y)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;+bc\:\text{Cov}(S,X)+bd\:\text{Cov}(S, Y)\]
  5. \[\text{Cov}(aX+bY,cX+dY)=ac\:\text{Var}(X)+ad\:\text{Var}(Y)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;+(ad+bc)\text{Cov}(X,Y)\]
  6. \(\text{Cov}(X+Y,X-Y)=\text{Var}(X)-\text{Var}(Y)\)
  7. If \(X, Y\) are independent. \(\text{Cov}(X,Y)=0\) But not vise-versa !

8.2 相关

  • 协方差虽然\(\text{Cov}(X,Y)\) 的大小很大程度上会被他们各自的单位和波动大小左右。
  • 我们将协方差标准化(除以各自的标准差 s.d.) (standardization) 之后，就可以得到相关系数 Corr (\(-1\sim1\)): \[\text{Corr}(X,Y)=\frac{\text{Cov}(X,Y)}{\text{SD}(X)\text{SD}(Y)}=\frac{\ text{Cov}(X,Y)}{\sqrt{\text{Var}(X)\text{Var}(Y)}}\]

8.3 中心极限定理

如果从人群中多次选出样本量为 \(n\) 的样本，并计算样本均值, \(\bar{X}_n\)。那么这个样本均值 \(\bar{X}_n\) 的分布，会随着样本量增加 \(n\rightarrow\infty\)，而接近正态分布。

伟大的中心极限定理告诉我们：

当样本量足够大时，样本均值 \(\bar{X}_n\) 的分布为正态分布，这个特性与样本来自的人群的分布 \(X_i\) 无关。

再说一遍：

如果对象是独立同分布 i.i.d (identically and independently distributed)。那么它的总体期望和方差分别是: \(E(X)=\mu;\;Var(X)=\sigma^2\)。 根据中心极限定理，可以得到：

  • 当样本量增加，样本均值的分布服从正态分布： \[\bar{X}_n\sim N(\mu, \frac{\sigma^2}{n})\]
  • 也可以写作，当样本量增加： \[\sum_{i=1}^nX_i \sim N(n\mu,n\sigma^2)\]
  • 有了这个定理，我们可以抛开样本空间(\(X\))的分布，也不用假定它服从正态分布。
  • 但是样本的均值，却总是服从正态分布的。简直是太完美了！！！

8.4 二项分布的正态分布近似

  • 假设我们有大量(\(n\rightarrow\infty\))的二项分布实验 \(X\sim Bin(n, \pi)\)

  • 根据二项分布的概率公式，计算将会变得很繁琐复杂。

  • 解决办法：应用中心极限定理。

  • 中心极限定理告诉我们，当样本量足够大时: \[X\sim N(n\pi, n\pi(1-\pi))\]

  • 问题在于，多大的 \(n\) 才能算大样本呢？

    • 当且仅当 (only and if only) \(n>20\) AND \(n\pi>5\) AND \(n(1-\pi)>5\)

8.5 泊松分布的正态分布近似

  • 假设时间 \(t\) 内某事件的发生次数服从泊松分布 \(X\sim Po(\mu)\)。

  • 考虑将这段时间 \(t\) 等分成 \(n\) 个时间段。那么第 \(i\) 时间段内事件发生次数依旧服从泊松分布 \(X_i\sim Po(\frac{\mu}{n})\)。且 \(E(X_i)=\mu/n, Var(X_i)=\mu/n\)。

  • 那么原先的 \(X\) 可以被视为是将这无数的小时间段的 \(X_i\) 相加。应用中心极限定理： \[X=\sum_{i=1}^nX_i\sim N(\frac{n\mu}{n}, \frac{n\mu}{n})\]

  • 需要注意的是，这段时间 (\(t\)) 内发生的事件次数 (\(\lambda\)) : \(\lambda t =\mu>10\) ，这样的正态分布模拟才能成立。

8.6 正态分布模拟的校正

  • 如果我们使用正态分布来模拟离散变量的分布，常常需要用到正态分布模拟的矫正。
  • 例如：我们如果用正态分布模拟来计算 \(P(X=15)\)，那么实际上我们应该计算的是 \(P(14.5<X<15.5)\)。

例: 1. 已知 \(X\sim Bin(100,0.5)\)，求 \(P(X>60)\)

解:

\[ \begin{aligned} \because X&\sim Bin(100, 0.5) \\ \therefore E(X) &=n\pi=50 \\ Var(X) &= n\pi(1-\pi) =25=5^2\\ P(X>60) &= 1-P(X\leqslant60) \\ &= 1-P(Z\leqslant\frac{60.5-50}{\sqrt{25}}) \\ &= 1-P(Z\leqslant2.1) \\ &= 1-\Phi(2.1) \\ &= 1-0.982 = 0.018 \end{aligned} \]

# 用r计算获得的概率：
1-pbinom(60, size=100, prob=0.5)
## [1] 0.0176001
# 用中心极限定理模拟正态分布获得的概率：
1-pnorm((60.5-50)/sqrt(25))
## [1] 0.01786442
## Warning in library(package, lib.loc = lib.loc, character.only = TRUE,
## logical.return = TRUE, : there is no package called 'ggfortify'
Probability of 60 successes out of 100 Binomial trials, probability of success = 0.75

图 8.1: Probability of 60 successes out of 100 Binomial trials, probability of success = 0.75

  1. 已知 \(X\sim Bin(48, 0.75)\), 求 \(P(30<X<39)\)

解

\[ \begin{aligned} \because B &\; \sim Bin(48, 0.75) \\ \therefore E(X) &\; =n\pi=36 \\ \text{Var}(X) &\; =n\pi(1-\pi)=9=3^2 \\ P(30<X<39) &\; = P(31\leqslant X\leqslant 38)\\ &\; = P(30.5\leqslant Y \leqslant 38.5) \\ Y\text{ is the }& \text{ normal approximation} \\ &\;= P(Y<38.5) - P(Y<30.5) \\ &\;= P(Z\leqslant\frac{38.5-36}{3})- P(Z\leqslant\frac{30.5-36}{3}) \\ &\;= P(Z\leqslant0.833) - P(Z\leqslant-1.833) \\ &\;= \Phi(0.833)-\Phi(-1.833) \\ &\;= 0.798-0.033 = 0.764 \end{aligned} \]

# 用r计算获得的概率：
pbinom(38, size=48, prob=0.75)-pbinom(30, size=48, prob=0.75)
## [1] 0.7578159
# 用中心极限定理模拟正态分布获得的概率：
pnorm((38.5-36)/sqrt(9)) - pnorm((30.5-36)/sqrt(9))
## [1] 0.7642951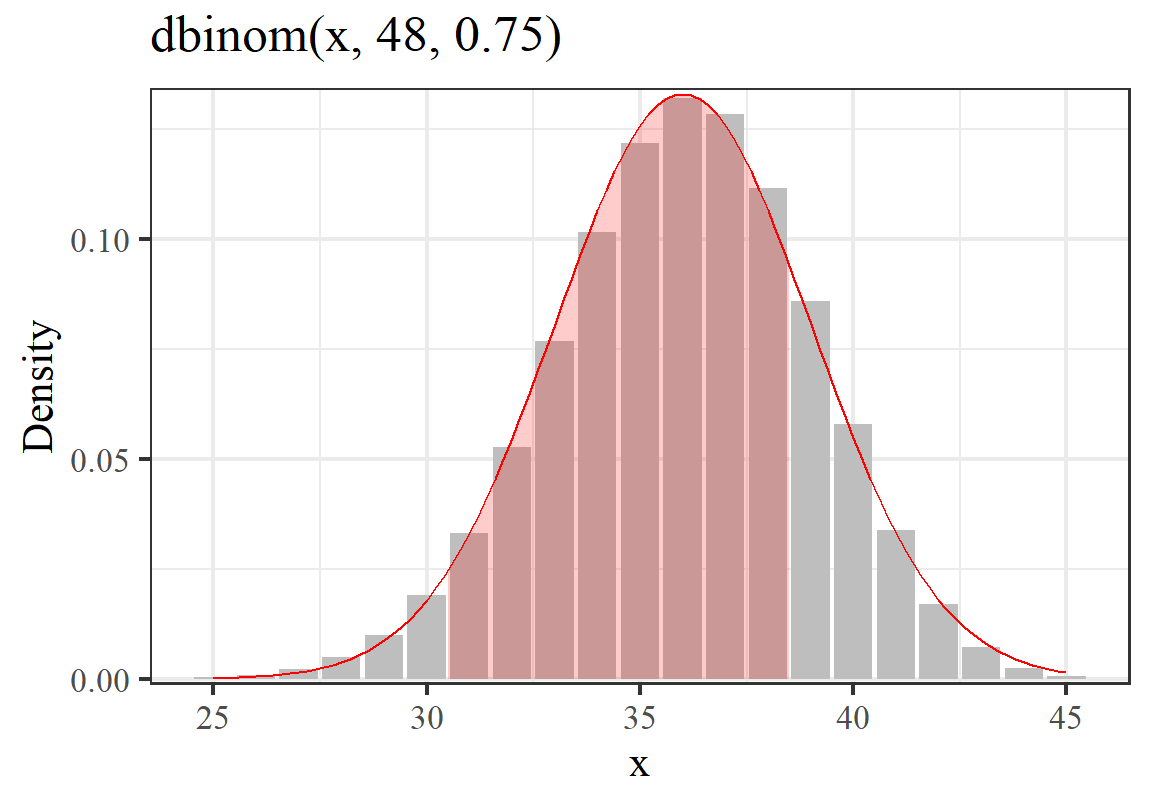
Probability of 30-39 successes out of 48 Binomial trials, probability of success = 0.75

图 8.2: Probability of 30-39 successes out of 48 Binomial trials, probability of success = 0.75

从上面两个例题也能看出，\(n\) 越小，正态分布模拟的误差就越大。

  1. 已知 \(X \sim Poisson(30)\) 求 \(P(X\leqslant20)\)。

解

\[ \because E(X)=\mu=30, \;Var(X)=\mu=30=(\sqrt{30})^2 \\ \begin{aligned} Pr(X\leqslant20) &= P(Z\leqslant\frac{20.5-30}{\sqrt{30}}) \\ &= P(Z\leqslant-1.734) \\ &= \Phi(-1.734) \\ &= 0.0414 \end{aligned} \]

# 际用r计算获得的概率：
ppois(20, lambda=30)
## [1] 0.03528462
# 用中心极限定理模拟正态分布获得的概率：
pnorm((20.5-30)/sqrt(30))
## [1] 0.04141871

这两个其实有些小差距。不过看下图，其模拟还是很到位的。只是正态分布的面积明显确实比泊松分布的小柱子面积要大一些。

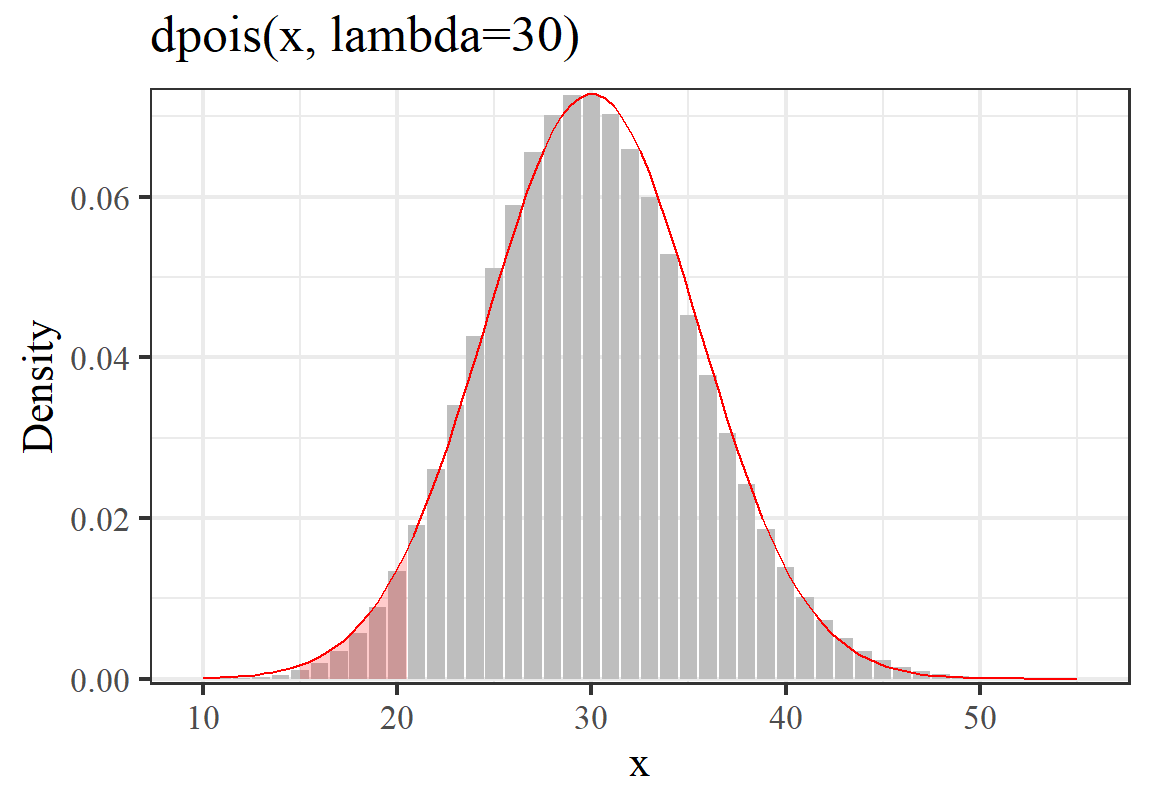
Probability of less than 20 events happen when the expectation is 30

图 8.3: Probability of less than 20 events happen when the expectation is 30

  1. 已知 \(X_1, X_2 \stackrel{i.i.d}{\sim} Poi(30)\) 求 \(P(X_1+X_2\leqslant40)\)。

解

\[ \begin{aligned} E(X_1+X_2) &\;= E(X_1)+E(X_2) = 30+30 = 60\\ Var(X_1+X_2) &\;= Var(X_1)+Var(X_2) = 30+30 \\ &\;= (\sqrt{60})^2 \\ P(X_1+X_2\leqslant 40) &\;= P(Z \leqslant \frac{40.5-60}{\sqrt{60}}) \\ &\;= P(Z\leqslant-2.517) \\ &\;= \Phi(-2.517) \\ &\;= 0.006 \end{aligned} \]

# 用r算法计算获得的概率：
ppois(40, lambda=60)
## [1] 0.00398281
# 用中心极限定理模拟正态分布获得的概率：
pnorm((40.5-60)/sqrt(60))
## [1] 0.005910569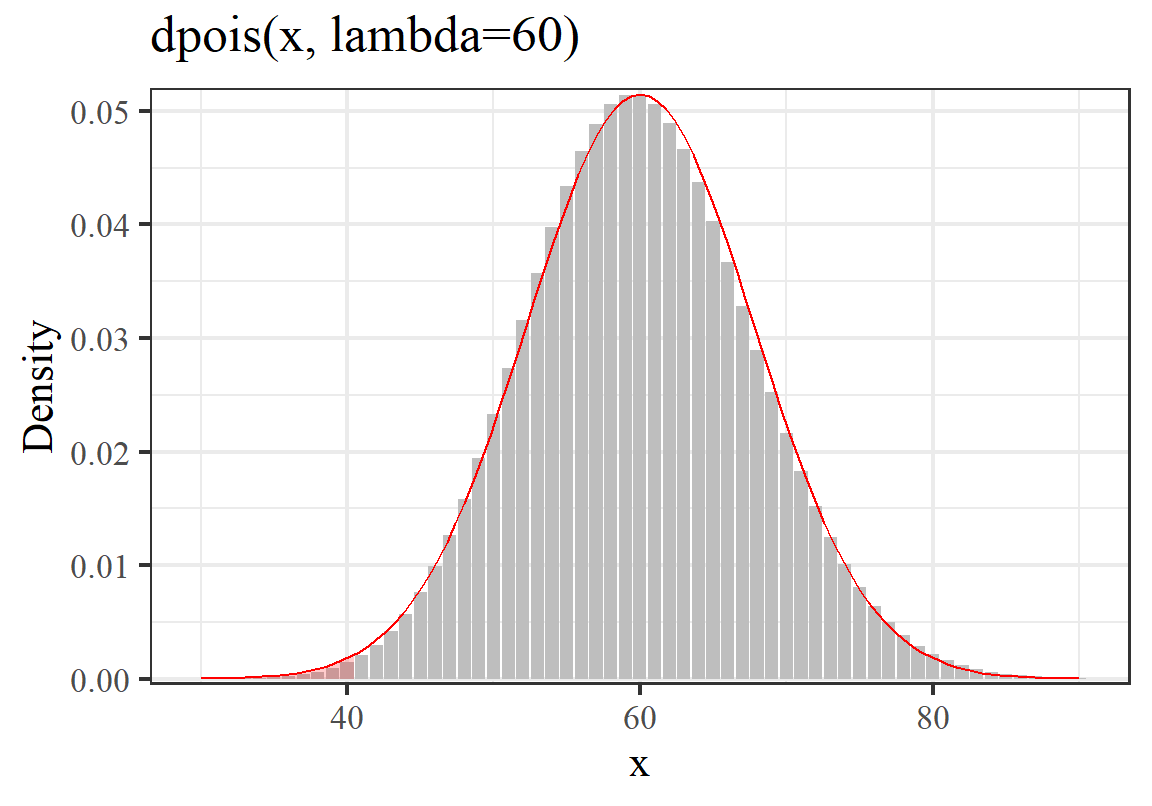
Probability of 2 identically and independently observed results of less or equal to 40 events happen in total when the expectation of each observation is 30

图 8.4: Probability of 2 identically and independently observed results of less or equal to 40 events happen in total when the expectation of each observation is 30

又一次，正态分布的面积比泊松分布的小柱子面积要大一些。

8.7 两个连续随机变量

  • 假定 \(X_1, X_2\) 是两个连续随机变量： \[ E(X_1)=\mu_1, \text{Var}(X_1)=\sigma_1^2 \\ E(X_2)=\mu_2, Var(X_2)=\sigma_2^2 \\ Corr(X_1, X_2)=\rho \Rightarrow \text{Cov}(X_1, X_2)=\rho\sigma_1\sigma_2=\sigma_{12} \]

  • 利用矩阵的标记法，可以将 \(X_1, X_2\) 标记为 \(\textbf{X}=(X_1, X_2)^T\), 即：

\[ \textbf{X}=\left( \begin{array}{c} X_1\\ X_2\\ \end{array} \right) \]

  • 上面的所有内容都可以标记为： \[ E(\textbf{X})=\mathbf{\mu}=\left( \begin{array}{c} \mu_1\\ \mu_2\\ \end{array} \right)\\ Covariance \;matrix: \\ Var(\textbf{X})=\mathbf{\Sigma}=\left( \begin{array}{c} \sigma_1^2 & \sigma_{12}\\ \sigma_{12} & \sigma_1^2\\ \end{array} \right) \]

8.8 两个连续随机变量的例子

假如要看收缩期血压 (\(SBP\)) 和舒张期血压 (\(DBP\)) 之间的关系：

下列为已知条件：

  • \(SBP\) 的均值为 \(130\)， 标准差为 \(15\);
  • \(DBP\) 的均值为 \(90\), 标准差为 \(10\);
  • \(SBP\) 和 \(DBP\) 之间的相关系数为 \(0.75\)。

那么， 我们可以把这些信息用下面的方法来标记：

\[ E(\textbf{X})=\mathbf{\mu}=\left( \begin{array}{c} 130\\ 90\\ \end{array} \right)\\ Var(\textbf{X})=\mathbf{\Sigma}=\left( \begin{array}{c} 225 & 112.5\\ 112.5 & 225\\ \end{array} \right) \]

8.9 条件分布和边缘分布的概念

  • 如果 \(\textbf{X}=(X_1, X_2)^T\) 的两个变量都服从正态分布；

  • 那么这两个变量的边缘分布 (marginal distribution) 也服从正态分布: \[X_1\sim N(\mu_1,\sigma_1^2), X_2\sim N(\mu, \sigma_2^2)\]

  • 同样的，\(X_1\) 的给出 \(X_2\) 的条件分布 (condition distribution) 也服从正态分布： \[E(X_1|X_2)=\mu_1+\frac{\rho\sigma_1}{\sigma_2}(X_2-\mu_2) \\ \text{Var}(X_1|X_2)=\sigma_1^2(1-\rho^2)\]

  • 反之亦然。

8.10 条件分布和边缘分布的例子

上面的概念过于抽象，用血压的例子：

收缩期血压和舒张期血压各自服从正态分布。那么可以用上面的概念来写出已知舒张期血压时，收缩期血压的分布。

  • 条件期望: \[E(\text{SBP|DBP})=130+\frac{0.75\times15}{10}(\text{DBP}-90)\]

  • 实际如果来了一个病人，他说他只记得自己测的舒张期血压是95：
    他的收缩期血压的期望值就可以用上面的式子计算： \[E(\text{SBP|DBP}=95)=136\]

  • 条件方差为： \[\text{Var}(\text{SBP|DBP})=15^2(1-0.75^2)=98.4\approx9.92^2<15^2\]

  • 所以当我们知道了这个人的一部分信息以后，推测他的另一个相关连的变量变得更加准确(方差变小)了。

8.10.1 实例

有 (闲) 人记录了 \(1494\) 名儿童在 \(2, 4, 6\) 岁时的腿长度。已知在记录的这三个年龄时的平均腿长度分别为 \(85 \text{ cm}, 103 { cm}, 114 { cm}\)。协方差矩阵如下:

\[ \left( \begin{array}{c} 22.2 & 11.8 & 13.7\\ 11.8 & 26.3 & 21.5\\ 13.7 & 21.5 & 29.0 \end{array} \right) \]

假定，这三个年龄记录的这些儿童的腿长度数据（联合分布, joint distribution）服从三个变量正态分布。

  1. 求 \(2\) 岁时这些儿童的腿长度的边缘分布 (marginal distribution)

解

\[X_{\text{age}=2} \sim N(85, \sigma_{\text{age}=2}^2=22.2)\]

  1. 求他们 \(6\) 岁时腿长度的 \(2\) 岁时的条件分布。 (Find the distribution of leg length age 6 conditional on leg length at age 2.)

解：

\(6\) 岁时和 \(2\) 岁时腿长的相关系数 (correlation, \(\rho_{6,2}\)) 为：

\[ \begin{aligned} \rho_{6,2} &= \frac{Cov_{6,2}}{\sqrt{\text{Var}(\text{length}_6)}\sqrt{\text{Var}(\text{length }_2)}}\\ &= \frac{13.7}{\sqrt{22.2}\sqrt{29}}=0.54 \end{aligned} \]

条件分布套用上面提到的公式：

\[ \begin{aligned} E({\text{length}_6 | \text{length}_2}) &= \mu_6+\frac{\rho_{6,2}\sigma_6}{\sigma_2}(\text{length}_2-\mu_2) \\ &= 114+\frac{0.54\times\sqrt{29.0}}{\sqrt{22.2}}(\text{length}_2-85)\\ \text{Var}(\text{length}_6 | \text{length}_2) &= \sigma_6^2(1-\rho_{6,2}^2) \\ &= 29.0\times(1-0.54^2) =20.5 \end{aligned} \]