第 49 章 随机回归系数模型
这一章节我们把随机截距模型进一步扩展,在随机效应部分增加随机斜率成分 (random slope)。这样的模型又称随机系数模型 (random coefficient model) 或 随机斜率模型 (random slope model)。
49.1 GCSE scores 实例
第一章介绍过的 65 所中学学生在入学前的阅读水平成绩和毕业时的考试成绩的 GCSE 数据,用来作为本章介绍概念的实例。我们先对其中学校编号为 1 的学生做两个成绩的线性回归:
library(haven)
library(tidyverse)
gcse_selected <- read_dta("../Datas/gcse_selected.dta")
M_sch1 <- lm(gcse ~ lrt, data = gcse_selected[gcse_selected$school == 1, ])
summary(M_sch1)##
## Call:
## lm(formula = gcse ~ lrt, data = gcse_selected[gcse_selected$school ==
## 1, ])
##
## Residuals:
## Min 1Q Median 3Q Max
## -22.488 -5.443 -1.018 6.193 15.469
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.83330 0.98224 3.903 0.000214 ***
## lrt 0.70934 0.09201 7.710 5.77e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.29 on 71 degrees of freedom
## Multiple R-squared: 0.4557, Adjusted R-squared: 0.448
## F-statistic: 59.44 on 1 and 71 DF, p-value: 5.771e-11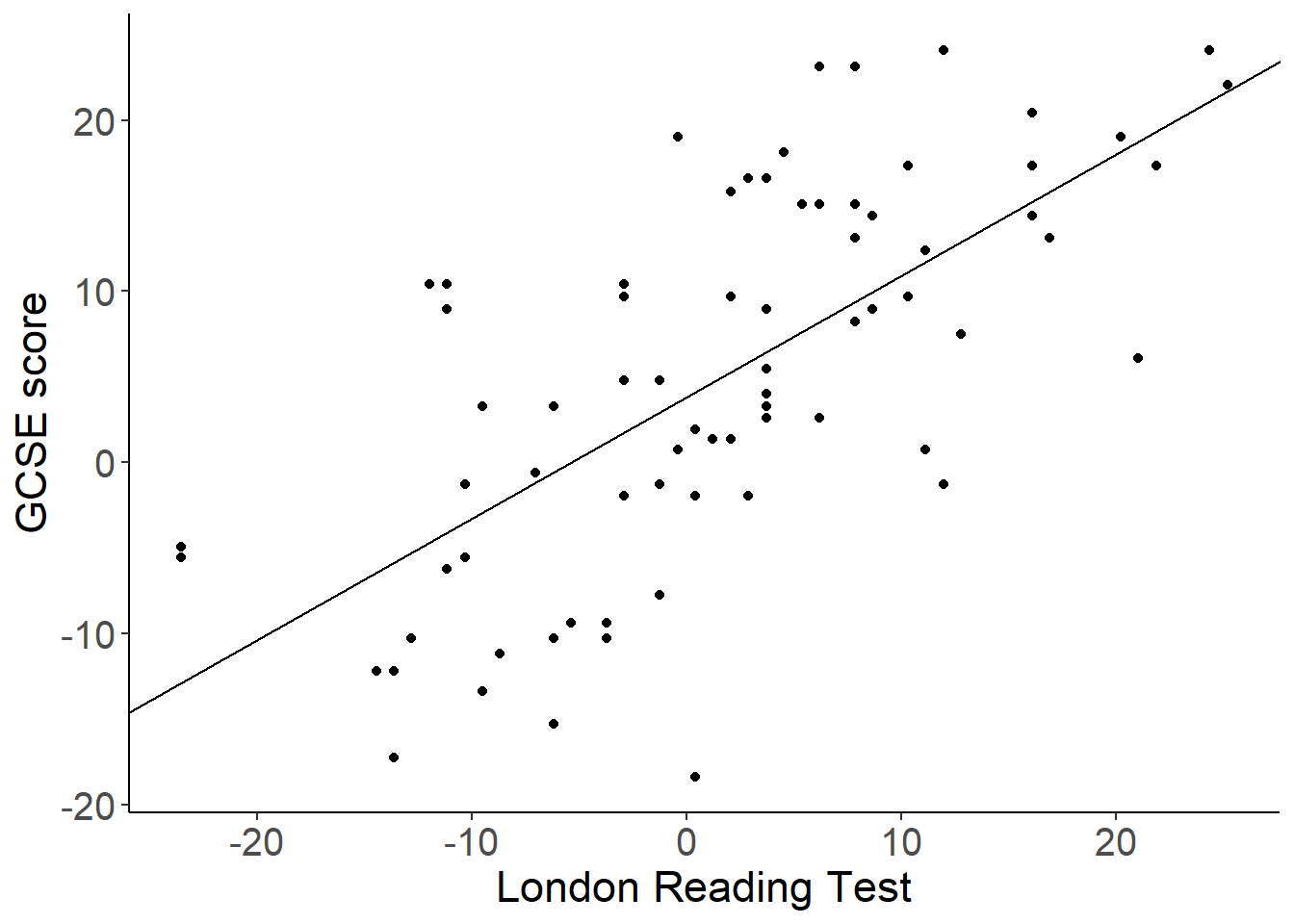
图 49.1: GCSE versus LRT in school 1
当我们重复同样的实验,给 65 所学校 (48号学校除外,它只有两个学生) 一一绘制回归直线的时候,你得到的一簇直线是这样纸的:
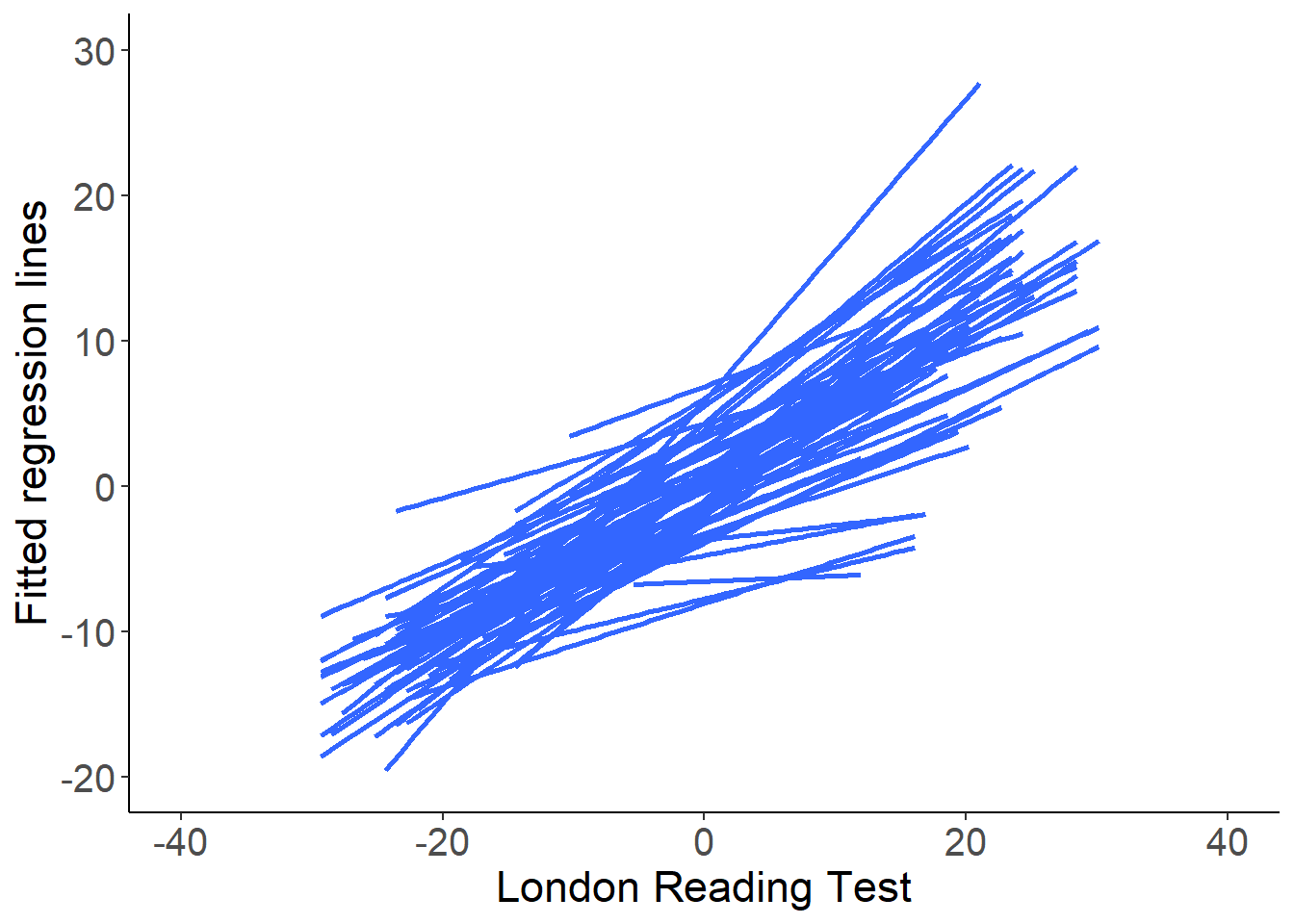
图 49.2: Predicted regression lines of GCSE versus LRT scores: separate estimates from each school
实际上这么多学校学生的成绩前后回归线,其截距和斜率各不相同 (图49.2)。这些斜率和截距的总结归纳如下:
##
## No. of observations = 64
##
## Var. name obs. mean median s.d. min. max.
## 1 (Intercept) 64 -0.18 -0.33 3.29 -8.52 6.84
## 2 lrt 64 0.54 0.54 0.18 0.04 1.08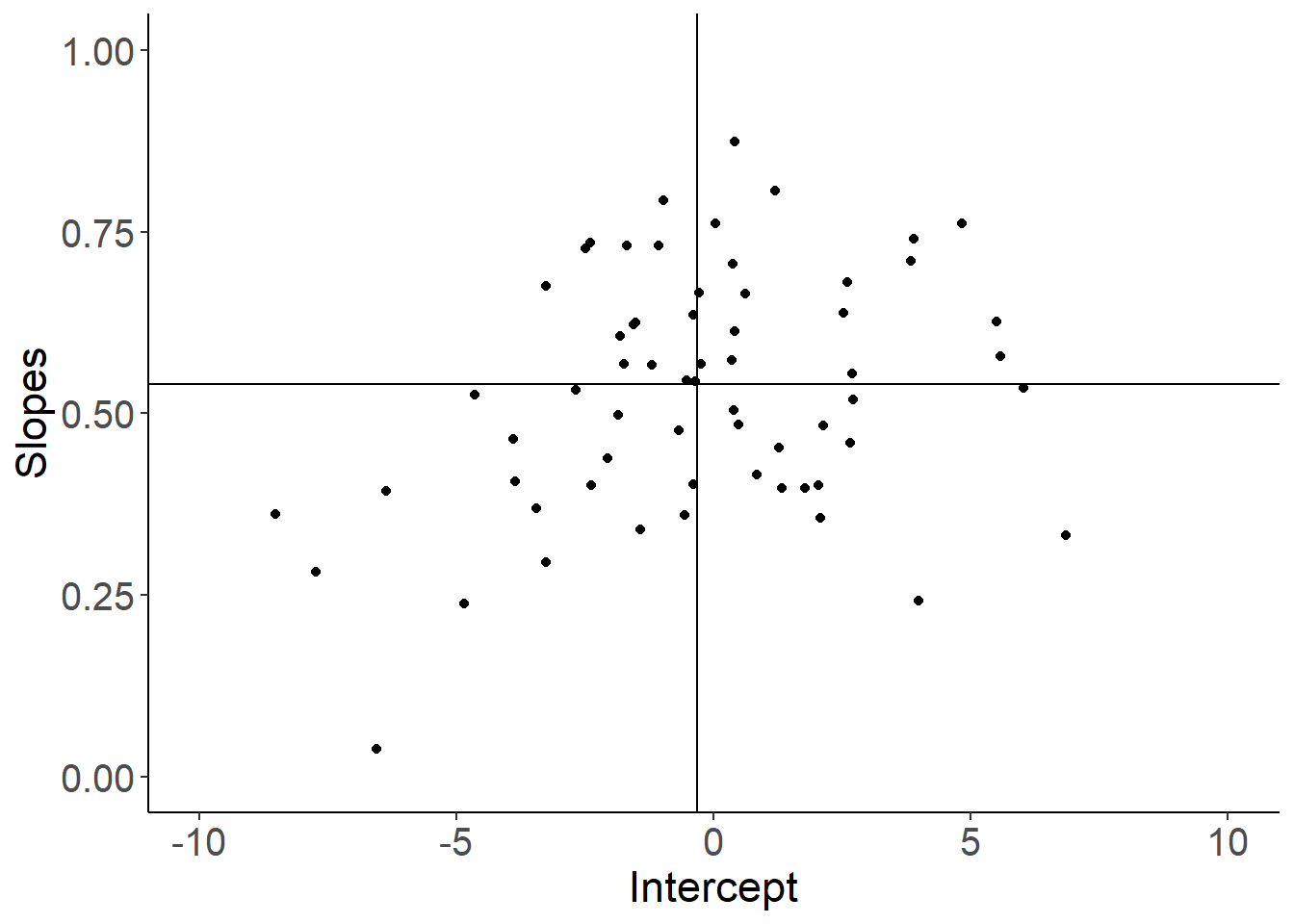
图 49.3: School specific slopes and intercepts
图 49.3 展示的是这些回归直线各自的截距 (x 轴) 和斜率 (y 轴) 的散点图。纵横添加的两条直线分别是截距和斜率的均值的位置。很明显,截距和斜率之间本身是呈现正相关的(相关系数0.36): 如果一个学校学生入学时成绩一般,但是毕业时GCSE 成绩较高,说明那所学校本身对学生成绩的提升作用明显。
经过拟合64个线性回归模型,获得 \(64\times3\) 个不同的回归线的参数 (截距,斜率,和残差方差)。所以我们可以提出的关于”学校” 这个个体,它们各自的入学前后成绩作出的回归线获得的三个参数,在它的“人群(可以是英国国内的中学,全欧洲的中学,或者是全世界的中学)” 中是随机分布在一些”均值” 附近的。
49.2 随机回归系数的实质
在随机截距模型中,截距可以随机分布在某个均值周围,但是每条回归直线我们默认其解释变量和结果变量之间的关系是一样的 (相同斜率的一簇直线)。现在,我们来把这个模型扩展,放宽它对斜率的限制,允许不同的层与层之间不仅仅可以有不同的截距,还可以有不同的斜率:
\[ \begin{equation} Y_{ij} = (\beta_0 + u_{0j}) + (\beta_1 + u_{1j})X_{1ij} + e_{ij} \end{equation} \tag{49.1} \]
其中:
- \(u_{0j}:\) 是随机截距成分 (第 \(j\) 层数据和总体均值 \(\beta_0\) 之间的差异)
- \(u_{1j}:\) 是随机斜率成分 (第 \(j\) 层数据和总体写率 \(\beta_1\) 之间的差异)
- \(\text{E}(u_{0j}|X_{1ij}) = 0\)
- \(\text{E}(u_{1j}|X_{1ij}) = 0\)
- \(\text{E}(e_{ij}|X_{1ij},u_{0j}, u_{1j}) = 0\)
- \(u_0, u_1 \perp X_{1ij}\) (两个随机部分和解释变量之间独立不相关)
- \(u_0, u_1 \perp e_{ij}\) (两个随机部分和总体的随机误差独立不相关)
另外,\(\mathbf{u}_j = \{u_0, u_1\}\) 服从分布:
\[ \mathbf{u}_j | X_{1ij} \sim N(\mathbf{0}, \mathbf{\sum}_{\mathbf{u}}) \]
其中的 \(\mathbf{\sum}_{\mathbf{u}}\) 是一个 \(2\times2\) 的方差协方差矩阵:
\[ \begin{aligned} \text{Where } \mathbf{u}_j & = (u_{0j}, u_{1j})^T \\ \mathbf{0}& = (0, 0)^T \\ \mathbf{\sum}_{\mathbf{u}} & =\left( \begin{array}{cc} \sigma^2_{u_{00}} & \sigma_{u_{01}} \\ \sigma_{u_{01}} & \sigma^2_{u_{11}} \\ \end{array} \right) \end{aligned} \]
\(e_{ij}\) 则服从下列分布:
\[ e_{ij} | X_{1ij}, u_{0j}, u_{1j} \sim N(0, \sigma^2_e) \]
49.3 继续 GCSE scores 实例
继续用 GCSE 数据,去除掉 48 号学校以后,拟合一个固定效应模型 (相同斜率,但是不同的固定截距):
FIX_inter <- lm(gcse ~ 0 + lrt + factor(school), data = gcse_selected[gcse_selected$school != 48, ])该固定效应模型 (简单线性回归模型) 估计的共同斜率是 0.56 (se = 0.01),和 64 个不同的固定斜率。这些固定斜率的范围是 -9,63 到 7.91,均值是 0.03,标准差是 3.38。估计的残差标准差是 Residual standard error: 7.52。
如果用相同的数据,我们允许截距发生随机变动的话 (随机截距模型):
MIX_inter <- lmer(gcse ~ lrt + (1 | school), data = gcse_selected[gcse_selected$school != 48, ], REML = TRUE)
summary(MIX_inter)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: gcse ~ lrt + (1 | school)
## Data: gcse_selected[gcse_selected$school != 48, ]
##
## REML criterion at convergence: 28044.1
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.7162 -0.6309 0.0292 0.6848 3.2666
##
## Random effects:
## Groups Name Variance Std.Dev.
## school (Intercept) 9.427 3.070
## Residual 56.605 7.524
## Number of obs: 4057, groups: school, 64
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 3.101e-02 4.053e-01 5.992e+01 0.077 0.939
## lrt 5.633e-01 1.247e-02 4.048e+03 45.168 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr)
## lrt 0.007随机截距模型估计的共同斜率还是不变 (0.56, se = 0.01),总体平均截距是 0.03 (无统计学意义)。截距的 (正态) 分布的标准差是 3.07。残差标准差,和刚才简单现行回归计算的残差标准差是一样的 (=7.52)。几乎所有我们关心的参数估计,都接近简单线性回归的结果,但是随机截距模型使用的参数个数只有 4 个,固定效应模型则用到了 66 个 (很显然随机截距模型更加高效)。
接下来,我们进一步拟合本章的重点模型 – 随机参数模型:
MIX_coef <- lmer(gcse ~ lrt + (lrt | school), data = gcse_selected[gcse_selected$school != 48, ], REML = TRUE)
summary(MIX_coef)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: gcse ~ lrt + (lrt | school)
## Data: gcse_selected[gcse_selected$school != 48, ]
##
## REML criterion at convergence: 28003
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.8318 -0.6320 0.0337 0.6833 3.4552
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## school (Intercept) 9.24988 3.0414
## lrt 0.01496 0.1223 0.49
## Residual 55.38239 7.4419
## Number of obs: 4057, groups: school, 64
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) -0.10918 0.40264 59.91325 -0.271 0.787
## lrt 0.55660 0.02011 56.33416 27.672 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr)
## lrt 0.365
## optimizer (nloptwrap) convergence code: 0 (OK)
## Model failed to converge with max|grad| = 0.00928374 (tol = 0.002, component 1)这个模型,不仅允许了随机的截距,还允许每个直线的斜率成为随机的斜率。此时的总体平均截距被估计为 -0.11 (依然没有统计学意义),标准差略微变小 (3.07 变成了 3.04)。总体平均斜率是 0.56,现在也被允许有变动,其标准差是 0.12。此时这些许许多多的估计回归方程中,斜率和截距的相关系数是 0.49,这十分接近我们在一开始的简单回归64次计算获得的斜率和截距的相关系数 (0.36)。此随机系数模型的残差标准差变成了 7.44,略微小于之前的 7.52。这三个模型的结果总结如下表:
49.4 使用模型结果推断
接下来,我们讨论如何比较随机系数模型,随机截距模型,也就是如何选择一个更优的模型。如果只是比较相同数据下,随机系数模型和随机截距模型的优劣,那么只需要同时检验\(u_{1j} = 0; \text{Cov}(u_{0j}, u_{1j}) = 0\) 。
就用刚刚拟合好的 MIX_inter 和 MIX_coef 来比较:
MIX_coef <- lme(fixed = gcse ~ lrt, random = ~ lrt | school, data = gcse_selected[gcse_selected$school != 48, ], method = "REML")
MIX_inter <- lme(fixed = gcse ~ lrt, random = ~ 1 | school, data = gcse_selected[gcse_selected$school != 48, ], method = "REML")
anova(MIX_inter, MIX_coef)## Model df AIC BIC logLik Test L.Ratio p-value
## MIX_inter 1 4 28052.05 28077.28 -14022.02
## MIX_coef 2 6 28014.96 28052.81 -14001.48 1 vs 2 41.08707 <.0001值得注意的是,这里计算的 似然比的检验统计量服从的是一个 自由度为 2 的卡方分布和一个 自由度为 1 的卡方分布的混合分布。所以报告中给出的 p 值是一个保守估计,正确的 p 值可以这样计算:
likelihood <- as.numeric(-2*(logLik(MIX_inter) - logLik(MIX_coef)))
0.5*(1-pchisq(as.numeric(likelihood), df = 1)) + 0.5*(1-pchisq(as.numeric(likelihood), df = 2))## [1] 6.712463e-10另一个重要的问题是该如何去真正理解这里随机系数模型给出的结果呢?
该模型的结果说,“人群”中的总体均值是 -0.11,总体斜率是 0.56 (se = 0.02, 95%CI: 0.52, 0.60)。这里的”人群”指的是全英国/或者全世界这样的学校。学校水平的截距和斜率服从以这两个数字为均值,标准差分别是 3.04 和 0.12 的正态分布。且截距和斜率之间的相关系数接近 0.50。第一层级 (学生的) 个体随机误差的标准差为 7.44。这些结果可以拿来估计”学校人群”的95% 截距/斜率: \(-0.11 \pm 1.96 \times3.04\) 和\(0.56 \pm 1.96\times0.12\),所以人群的截距的95%信赖区间是: \(-6.07, 5.85\),斜率的95% 信赖区间是: \(0.33, 0.80\)。与此形成对比的是,我们开头给64 所学校建立的64 个模型的截距和斜率拿来估计的95% 截距信赖区间是\(-0.18 \pm 1.96\times3.29: -6.63, 6.27\) ,95% 斜率信赖区间是\(0.54 \pm 1.96 \times 0.18: 0.19, 0.89\)。所以,随机系数模型对截距和斜率的人群估计及推断更加精准。
49.5 随机效应的方差
在解释混合效应模型的随机效应部分的时候,有几点需要注意。首先,随机截距的方差,和随机斜率的方差,是具有不同单位的。 随机截距的方差的单位是结果变量 \(Y\) 的单位的平方。 随机斜率的方差,是结果变量和解释变量的单位的商的平方。
另一个要注意的点是,\(Y_{ij}\) 在 \(X_{1ij}\) 的条件下的残差的标准差,不是恒定不变的 (随着 \(X_1\) 的变化而变化):
\[ \begin{aligned} Y_{ij} & = (\beta_0 + u_{0j}) + (\beta_1 + u_{1j}) X_{1ij} + e_{ij} \\ & = (\beta_0 + \beta_1X_{1ij}) + (u_{0j} + u_{1j}X_{1ij} + e_{ij}) \\ & = (\beta_0 + \beta_1X_{1ij}) + \epsilon_{ij} \end{aligned} \]
所以从上面的式子可看出,随机参数模型的总体残差(total residuals),\(\epsilon_{ij} = u_{0j} + u_{1j}X_{1ij} + e_{ij }\),是随着你想给斜率随机性的那个解释变量的变化而变化的。也正因为如此,总体残差的方差,也是随着解释变量变化而变化的(和解释变量成二次方程关系,如果绘制总体惨差的方差和解释变量之间的关系会是一个抛物线):
\[ \begin{aligned} \text{Var}(Y_{ij} | X_{1ij}) & = \text{Var}( u_{0j} + u_{1j}X_{1ij} + e_{ij}) \\ & = \sigma^2_{u_{00}} + X_{1ij}^2\sigma^2_{u_{11}} + 2X_{1ij}\sigma_{u_{01}} + \sigma^2_e \end{aligned} \tag{49.2} \]
49.6 模型效果评估
拟合模型的评估中,另一个重要的事是分析第一阶层残差和第二阶层残差是不是符合其前提条件 (正态分布)。记得第二阶层残差获取之后需要被标准化。
MIX_coef <- lme4::lmer(gcse ~ lrt + (lrt | school), data = gcse_selected[gcse_selected$school != 48, ], REML = TRUE)
School_res0 <- HLMdiag::hlm_resid(MIX_coef, level = "school", type = "EB", standardize = FALSE)
summ.data.frame(School_res0)##
## No. of observations = 64
##
## Var. name obs. mean median s.d. min. max.
## 1 school
## 2 .ranef.intercept 64 0 -0.11 2.87 -7.19 6.45
## 3 .ranef.lrt 64 0 0 0.1 -0.19 0.35
## 4 .ls.intercept 64 0 -0.14 3.29 -8.34 7.02
## 5 .ls.lrt 64 0 0 0.18 -0.5 0.54School_res1 <- HLMdiag::hlm_resid(MIX_coef, level = "school", type = "EB", standardize = TRUE)
summ.data.frame(School_res1)##
## No. of observations = 64
##
## Var. name obs. mean median s.d. min. max.
## 1 school
## 2 .std.ranef.intercept 64 0.04 -0.14 3 -6.74 7.53
## 3 .std.ranef.lrt 64 0.04 -0.03 1.31 -2.35 5.07
## 4 .std.ls.intercept 64 0 -0.04 1 -2.53 2.13
## 5 .std.ls.lrt 64 0 0 1 -2.84 3.05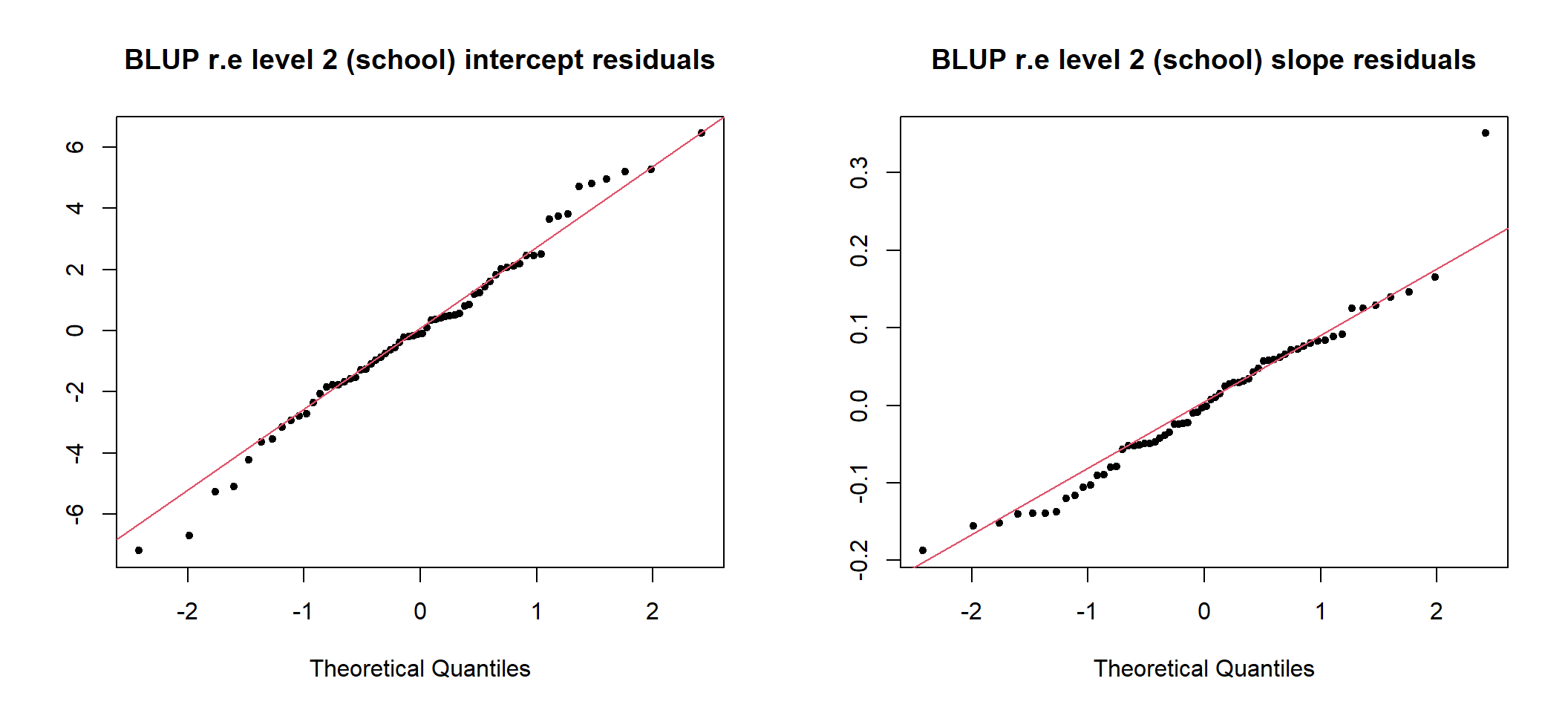
图 49.4: Q-Q plots of school level intercept and slope residuals (unstandardized)
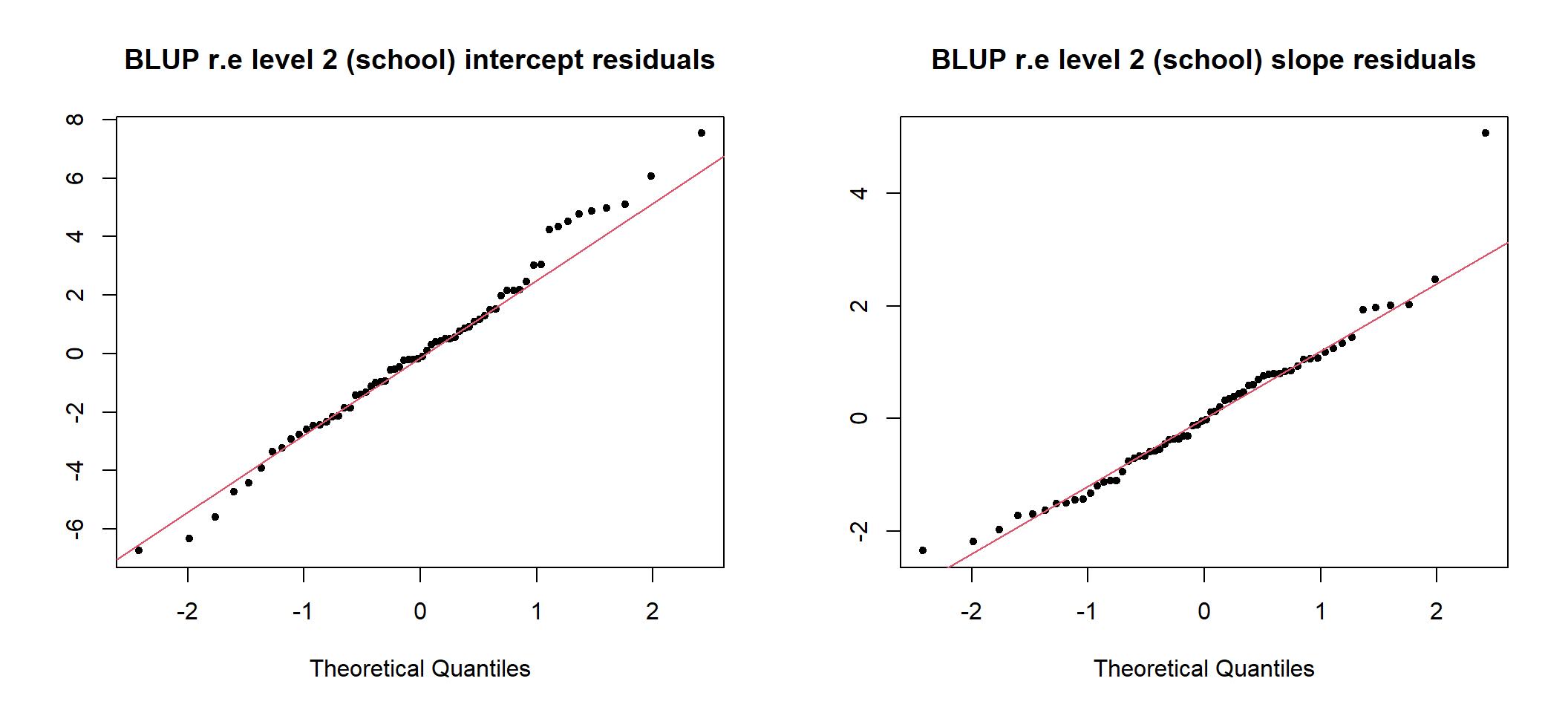
图 49.5: Q-Q plots of school level intercept and slope residuals (standardized)
## obs. mean median s.d. min. max.
## 4057 0 0.034 0.989 -3.832 3.455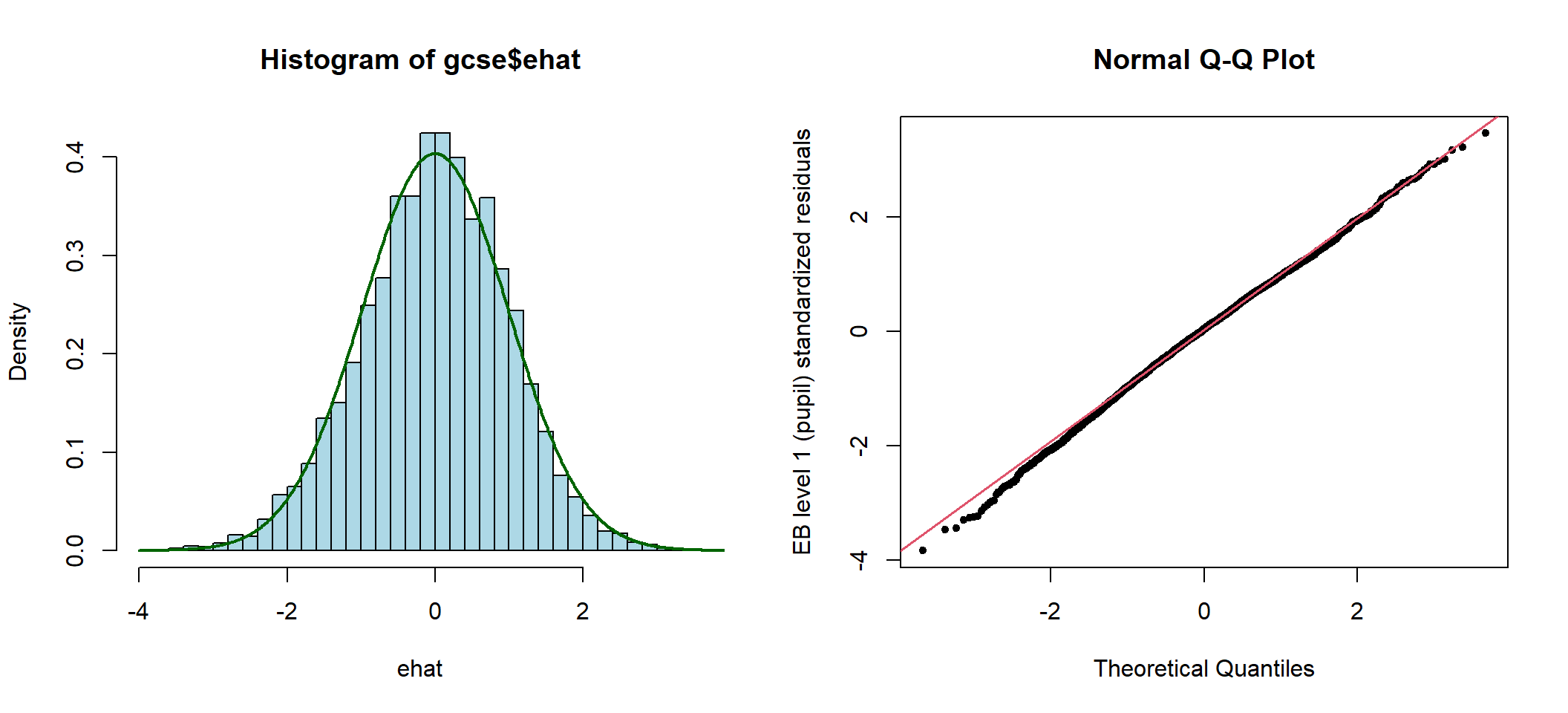
图 49.6: Histogram and Q-Q plots of elementary level (pupil) standardized residuals
49.7 Hierarchical例4
- GCSE data: 数据来自65所中学的学生毕业成绩 “the Graduate Certificate of Secondary Education (GCSE) score”,和这些学生在刚刚入学时接受阅读能力水平测试 (LRT score) 的成绩。其变量和各自含义为:
school school identifier
student student identifier
gcse GCSE score (multiplied by 10)
lrt LRT score (multiplied by 10)
girl Student female gender (1 = yes, 0 = no)
schgend type of school (1: mixed gender; 2: boys only; 3: girls only)### 将数据导入软件里,
gcse_selected <- read_dta("../backupfiles/gcse_selected.dta")
length(unique(gcse_selected$school)) ## number of school = 65## [1] 65gcse_selected <- gcse_selected %>%
mutate(schgend = factor(schgend, labels = c("mixed geder", "boys only", "girls only")))
## create a subset data with only the first observation of each school
gcse <- gcse_selected[!duplicated(gcse_selected$school), ]
# 一共有 65 所学校,54% 是混合校,15% 是男校,31% 是女校
with(gcse, tab1(schgend, graph = FALSE))## schgend :
## Frequency Percent Cum. percent
## mixed geder 35 53.8 53.8
## boys only 10 15.4 69.2
## girls only 20 30.8 100.0
## Total 65 100.0 100.0# 计算每所学校两种成绩的平均分,计算一个包含每所学校的平均女生人数的变量
Mean_gcse_lrt <- plyr::ddply(gcse_selected,~school,summarise,mean_gcse=mean(gcse),mean_lrt=mean(lrt), mean_girl=mean(girl))
# 整体来说,GCSE 分数的分布比起入学前 LRT 分数的分布更加宽泛,标准差更大。
# 意味着入学时学生阅读成绩的差异,比起毕业时成绩的差异要小。
# 或者反过来说,毕业时成绩差异,比起入学时阅读成绩的差异要大。
epiDisplay::summ(Mean_gcse_lrt[,2:4])##
## No. of observations = 65
##
## Var. name obs. mean median s.d. min. max.
## 1 mean_gcse 65 -0.23 -0.34 4.39 -10.49 10.04
## 2 mean_lrt 65 -0.31 -0.41 3.44 -7.56 6.38
## 3 mean_girl 65 0.57 0.5 0.36 0 149.7.1 先忽略学校编号为 48 的学校,拟合一个只有固定效应 (简单线性回归模型),结果变量是 GCSE,解释变量是 LRT 和学校。
Fix <- lm(gcse ~ lrt + factor(school), data = gcse_selected[gcse_selected$school !=48, ])
anova(Fix)## Analysis of Variance Table
##
## Response: gcse
## Df Sum Sq Mean Sq F value Pr(>F)
## lrt 1 141723 141723 2505.000 < 2.2e-16 ***
## factor(school) 63 37315 592 10.469 < 2.2e-16 ***
## Residuals 3992 225852 57
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1LRT 的回归系数 (直线斜率 = 0.56, se = 0.01),残差的标准差 \(\hat\sigma_e =\) 7.52。
Call:
lm(formula = gcse ~ lrt + factor(school), data = gcse_selected[gcse_selected$school !=
48, ])
Residuals:
Min 1Q Median 3Q Max
-28.32 -4.77 0.22 5.08 24.41
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.08232 0.88060 4.64 3.7e-06 ***
lrt 0.55948 0.01253 44.63 < 2e-16 ***
factor(school)2 1.53785 1.34332 1.14 0.25235
...
...<OMITTED OUTPUT>
...
...
factor(school)65 -5.85245 1.21850 -4.80 1.6e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.52 on 3992 degrees of freedom
Multiple R-squared: 0.442, Adjusted R-squared: 0.433
F-statistic: 49.4 on 64 and 3992 DF, p-value: <2e-1649.7.2 仅有固定效应模型的学校变量变更为学校类型(男校女校或混合校),从这个新模型的结果来看,你是否认为学校类型,和学校编号本身相比能够解释相同的学校层面的方差? lrt 的估计回归参数发生了怎样的变化?
## Analysis of Variance Table
##
## Response: gcse
## Df Sum Sq Mean Sq F value Pr(>F)
## lrt 1 141723 141723 2222.602 < 2.2e-16 ***
## schgend 2 4729 2364 37.081 < 2.2e-16 ***
## Residuals 4053 258438 64
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = gcse ~ lrt + schgend, data = gcse_selected[gcse_selected$school !=
## 48, ])
##
## Residuals:
## Min 1Q Median 3Q Max
## -26.1754 -5.1241 0.1917 5.3540 28.3223
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.96087 0.17146 -5.604 2.23e-08 ***
## lrt 0.59427 0.01262 47.084 < 2e-16 ***
## schgendboys only 1.17771 0.39204 3.004 0.00268 **
## schgendgirls only 2.36292 0.27527 8.584 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.985 on 4053 degrees of freedom
## Multiple R-squared: 0.3617, Adjusted R-squared: 0.3612
## F-statistic: 765.6 on 3 and 4053 DF, p-value: < 2.2e-16新的模型 Fix1 参数明显减少很多,残差标准差估计 \(\hat\sigma_u =\) 7.99。 LRT 的回归系数估计仅发生了不太明显的变化 0.59 (0.01)
49.7.3 使用限制性极大似然法拟合一个随机截距模型。记录此时的限制性对数似然的大小 (log-likelihood)。用 lmerTest::rand 命令对随机效应部分的方差是否为零做检验,指明该检验的零假设是什么,并解释其结果的含义。
library(lmerTest)
Fixed_reml <- lmer(gcse ~ lrt + (1 | school), data = gcse_selected[gcse_selected$school !=48, ], REML = TRUE)
summary(Fixed_reml)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: gcse ~ lrt + (1 | school)
## Data: gcse_selected[gcse_selected$school != 48, ]
##
## REML criterion at convergence: 28044.1
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.7162 -0.6309 0.0292 0.6848 3.2666
##
## Random effects:
## Groups Name Variance Std.Dev.
## school (Intercept) 9.427 3.070
## Residual 56.605 7.524
## Number of obs: 4057, groups: school, 64
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 3.101e-02 4.053e-01 5.992e+01 0.077 0.939
## lrt 5.633e-01 1.247e-02 4.048e+03 45.168 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr)
## lrt 0.007## ANOVA-like table for random-effects: Single term deletions
##
## Model:
## gcse ~ lrt + (1 | school)
## npar logLik AIC LRT Df Pr(>Chisq)
## <none> 4 -14022 28052
## (1 | school) 3 -14225 28456 405.6 1 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1随机截距模型的输出结果可以看出,这里的混合模型估计的 LRT 的回归系数跟仅有固定效应的简单线性回归模型估计的值完全一样 (0.56, se=0.01)。随机效应部分 \(\hat\sigma_e = 7.524, \hat\sigma_u = 3.07\),此时的限制性似然 (restricted log-likelihood) 是 -14022。最晚部分的随机效应检验的零假设是\(\sigma_u = 0\),且值得注意的是,由于方差本身不可能小于零,故本次检验只用到自由度为1 的卡方分布的右半侧(单侧)。也就是说,其替代假设有且只有 \(\sigma_u > 0\) 的单侧假设。这里的检验结果提示高度有意义 (highly significant)。
49.7.4 在前一题的随机截距模型中加入 schgend 变量,作为解释随机截距的一个自变量,观察输出结果,解释其是否有意义。记录这个模型的限制性似然。
Fixed_reml1 <- lmer(gcse ~ lrt + schgend + (1 | school), data = gcse_selected[gcse_selected$school !=48, ], REML = TRUE)
#Fixed_reml1 <- lme(fixed = gcse ~ lrt + schgend , random = ~ 1 | school, data = gcse_selected[gcse_selected$school !=48, ], method = "REML")
summary(Fixed_reml1)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: gcse ~ lrt + schgend + (1 | school)
## Data: gcse_selected[gcse_selected$school != 48, ]
##
## REML criterion at convergence: 28032.6
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.7122 -0.6302 0.0265 0.6806 3.2445
##
## Random effects:
## Groups Name Variance Std.Dev.
## school (Intercept) 8.496 2.915
## Residual 56.605 7.524
## Number of obs: 4057, groups: school, 64
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) -0.87266 0.52498 58.50425 -1.662 0.1018
## lrt 0.56351 0.01246 4049.31627 45.209 <2e-16 ***
## schgendboys only 0.96868 1.11817 59.75279 0.866 0.3898
## schgendgirls only 2.49782 0.87661 56.67655 2.849 0.0061 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) lrt schgndbo
## lrt 0.006
## schgndbyson -0.469 0.006
## schgndgrlso -0.599 -0.004 0.281## 检验新增的学校种类 schgend 是否对应该加入模型。
mod2<- update(Fixed_reml1, . ~ . - schgend)
anova(Fixed_reml1, mod2)## Data: gcse_selected[gcse_selected$school != 48, ]
## Models:
## mod2: gcse ~ lrt + (1 | school)
## Fixed_reml1: gcse ~ lrt + schgend + (1 | school)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## mod2 4 28045 28070 -14019 28037
## Fixed_reml1 6 28041 28079 -14015 28029 8.0185 2 0.01815 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## 'log Lik.' -14016.32 (df=6)增加了学校类型在固定效应部分时,随机效应的标准差从钱一个模型的 3.07 降低到这里的 2.92。这个变量本身,从最后的模型比较也能看出,对模型的贡献是有意义的 (p=0.018)。当然从随机截距模型的输出结果可以看出,学校类型的这一变量中,可能只有”女校”这一细分部分提供了足够的效应。这里的随机截距模型的REML似然是 (restricted log-likelihood = -14016)
49.7.5 拟合随机截距随机斜率模型,固定效应部分的 lrt 也加入进随机效应部分。
Fixed_reml2 <- lmer(gcse ~ lrt + schgend + (lrt | school), data = gcse_selected[gcse_selected$school !=48, ], REML = TRUE)
summary(Fixed_reml2)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: gcse ~ lrt + schgend + (lrt | school)
## Data: gcse_selected[gcse_selected$school != 48, ]
##
## REML criterion at convergence: 27988.8
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.8307 -0.6301 0.0325 0.6850 3.4166
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## school (Intercept) 8.27319 2.8763
## lrt 0.01494 0.1222 0.58
## Residual 55.39403 7.4427
## Number of obs: 4057, groups: school, 64
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) -1.09782 0.49754 63.00986 -2.206 0.03100 *
## lrt 0.55820 0.02007 56.23839 27.807 < 2e-16 ***
## schgendboys only 1.04152 0.99885 57.08401 1.043 0.30147
## schgendgirls only 2.71202 0.78349 53.76367 3.461 0.00106 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) lrt schgndbo
## lrt 0.321
## schgndbyson -0.443 0.011
## schgndgrlso -0.566 0.011 0.284## 'log Lik.' -13994.39 (df=8)当截距(不同学校之间, gcse 的起点),斜率(不同学校之间lrt 和gcse 之间的关系的斜率) 均可以有随机性以后,lrt 的斜率虽然仍然保持不变$=0.56 \(,但是它的随机效应标准差变成了\)=0.12\(,随机截距的标准差也保持不变\)=2.88\(,这二者之间的相关系数是\)=0.58$。第一阶层随机残差标准也有了微妙的变化 \(7.52 \rightarrow 7.44\),此模型的限制性对数似然 (restricted log-likelihood) 是 -13994.393 (df=8)。
49.7.6 通过上面几个模型计算获得的似然,尝试检验随机斜率标准差,以及该标准差和随机截距标准差的协相关是否有意义。
## ANOVA-like table for random-effects: Single term deletions
##
## Model:
## gcse ~ lrt + schgend + (lrt | school)
## npar logLik AIC LRT Df Pr(>Chisq)
## <none> 8 -13994 28005
## lrt in (lrt | school) 6 -14016 28045 43.855 2 2.999e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# 手算的方法是这样的likelihood <- as.numeric(-2*(logLik(Fixed_reml1) - logLik(Fixed_reml2)))
0.5*(1-pchisq(as.numeric(likelihood), df = 1)) + 0.5*(1-pchisq(as.numeric(likelihood), df = 2))## [1] 6.712463e-10似然比检验的统计量是 43.8,不用检验也知道肯定是有意义的。手算也是可以达到相同的效果。值得注意的是,R计算给出的基于自由度为 2 的卡方分布,其实是偏保守的。注意看手算部分,其实用到了自由度为 1 自由度为 2 两个卡方分布换算获得的 p 值。
49.7.7 模型中的 schgend 改成 mean_girl 会给出怎样的结果呢?
## 把女生平均值放回整体数据中去
Mean_girl <- NULL
for (i in 1:65) {
Mean_girl <- c(Mean_girl, rep(Mean_gcse_lrt$mean_girl[i], with(gcse_selected, table(school))[i]))
}
gcse_selected$mean_girl <- Mean_girl
rm(Mean_girl)
Fixed_reml3 <- lmer(gcse ~ lrt + mean_girl + (lrt | school), data = gcse_selected[gcse_selected$school !=48, ], REML = TRUE)## Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
## Model failed to converge with max|grad| = 0.0133708 (tol = 0.002, component 1)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: gcse ~ lrt + mean_girl + (lrt | school)
## Data: gcse_selected[gcse_selected$school != 48, ]
##
## REML criterion at convergence: 27997.1
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.8196 -0.6317 0.0299 0.6844 3.4351
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## school (Intercept) 8.91069 2.9851
## lrt 0.01491 0.1221 0.52
## Residual 55.38858 7.4424
## Number of obs: 4057, groups: school, 64
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) -1.28001 0.70547 63.12262 -1.814 0.0744 .
## lrt 0.55671 0.02008 56.13401 27.719 <2e-16 ***
## mean_girl 2.06616 1.03154 56.69399 2.003 0.0500 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) lrt
## lrt 0.220
## mean_girl -0.828 -0.004
## optimizer (nloptwrap) convergence code: 0 (OK)
## Model failed to converge with max|grad| = 0.0133708 (tol = 0.002, component 1)由于 mean_girl 其实是和 schgend 非常相似的表示学校层面的男女生性别比例的变量,所以这个模型的结果其实和前一个给出的随机效应标准差的估计都很接近。
49.7.8 现在我们把注意力改为关心学校编号为 48 的学校的情况。用且禁用它一所学校的数据,拟合一个简单线性回归,结果变量是 gcse,解释变量是 lrt。
## # A tibble: 2 × 7
## school student gcse lrt girl schgend mean_girl
## <dbl> <dbl> <dbl> <dbl> <dbl> <fct> <dbl>
## 1 48 1 -7.00 -3.73 1 girls only 1
## 2 48 2 -1.29 -4.55 1 girls only 1##
## Call:
## lm(formula = gcse ~ lrt, data = gcse_selected[gcse_selected$school ==
## 48, ])
##
## Residuals:
## ALL 2 residuals are 0: no residual degrees of freedom!
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -32.722 NaN NaN NaN
## lrt -6.902 NaN NaN NaN
##
## Residual standard error: NaN on 0 degrees of freedom
## Multiple R-squared: 1, Adjusted R-squared: NaN
## F-statistic: NaN on 1 and 0 DF, p-value: NA由于 48 号学校只有两个数据点,所以强行进行简单线性回归的结果,就是拟合了一条通过这两个点的直线,截距是-32.7,斜率是 -6.9,且没有任何估计的误差。
49.7.9 这次不排除 48 号学校,拟合所有学校的数据进入 Fixed_reml2 模型中去,结果有发生显著的变化吗?
## Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
## Model failed to converge with max|grad| = 0.00818778 (tol = 0.002, component 1)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: gcse ~ lrt + schgend + (lrt | school)
## Data: gcse_selected
##
## REML criterion at convergence: 28001.4
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.8312 -0.6310 0.0328 0.6853 3.4186
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## school (Intercept) 8.24885 2.8721
## lrt 0.01497 0.1223 0.58
## Residual 55.37679 7.4416
## Number of obs: 4059, groups: school, 65
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) -1.09913 0.49690 63.30631 -2.212 0.03059 *
## lrt 0.55801 0.02008 56.23072 27.788 < 2e-16 ***
## schgendboys only 1.04105 0.99765 57.33868 1.044 0.30109
## schgendgirls only 2.67280 0.77971 54.62568 3.428 0.00116 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) lrt schgndbo
## lrt 0.321
## schgndbyson -0.443 0.011
## schgndgrlso -0.569 0.010 0.285
## optimizer (nloptwrap) convergence code: 0 (OK)
## Model failed to converge with max|grad| = 0.00818778 (tol = 0.002, component 1)可以看到,即使我们加入这个数据量极少的一个学校的数据,对结果也没有太大的影响。
49.7.10 计算这个模型的第二阶级(level 2, school level)的残差。
School_res <- HLMdiag::hlm_resid(Fixed_reml2, level = "school", include.ls = FALSE)
epiDisplay::summ(School_res)##
## No. of observations = 65
##
## Var. name obs. mean median s.d. min. max.
## 1 school
## 2 .ranef.intercept 65 0 0.11 2.65 -6.25 5.83
## 3 .ranef.lrt 65 0 0 0.1 -0.19 0.33## # A tibble: 1 × 3
## school .ranef.intercept .ranef.lrt
## <chr> <dbl> <dbl>
## 1 48 -0.739 -0.0147随机截距的残差估计范围在 -6.25 和 5.83 之间,随机斜率残差估计范围在 -0.19 和 0.33 之间。其中 48 号学校的拟合后截距和斜率分别是 -0.74 和 -0.02。48 号学校在这个模型中估计的截距和斜率,与我们单独对它一所学校拟合模型时的结果大相径庭。这是因为在总体的混合效应模型中,该学校的数据被拉近与总体的平均水平。
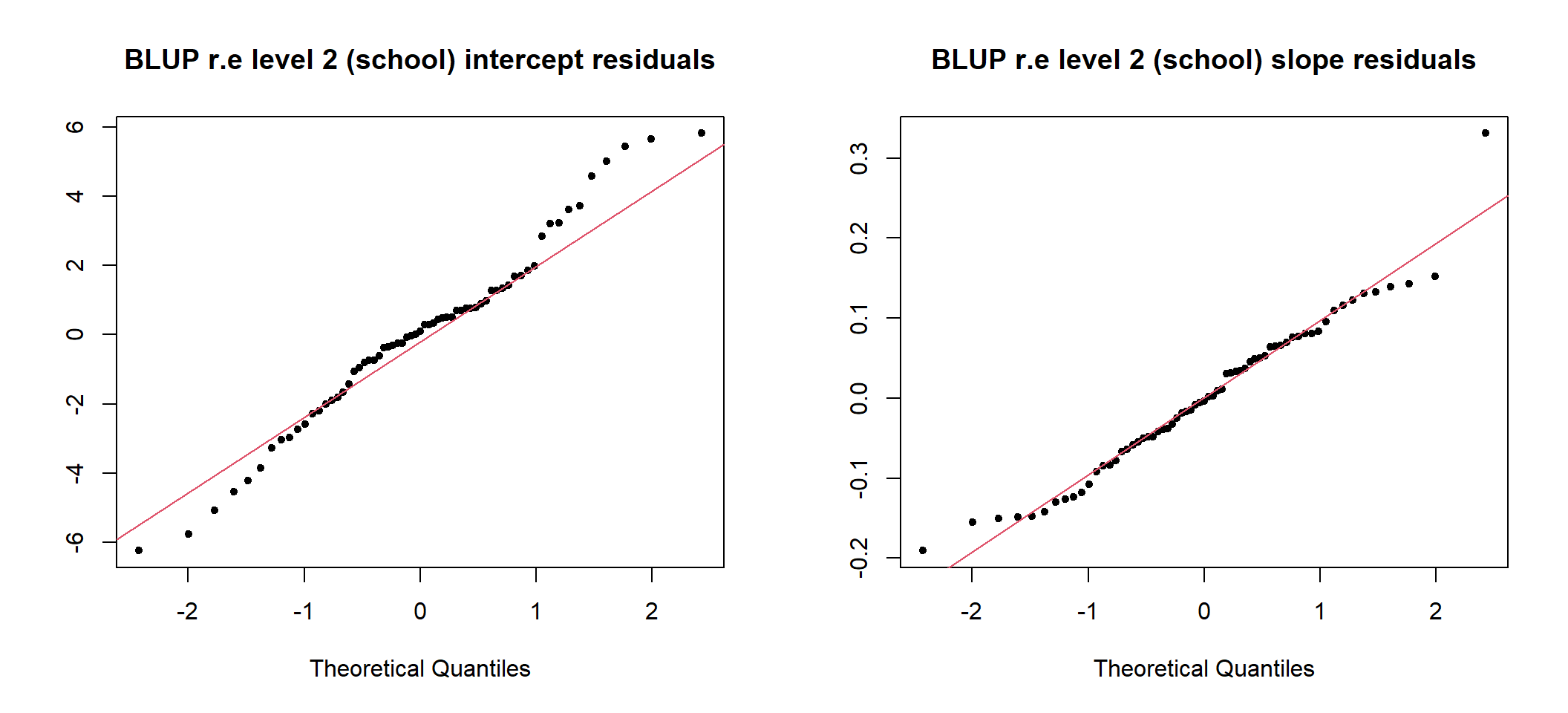
图 49.7: Q-Q plots of school level intercept and slope (unstandardized) residuals
图 49.7 显示标准化前的随机效应部分的残差表现尚可接受。
49.7.11 计算这个模型的第一阶级(level 1, student)残差,分析其分布,查看第48所学校的残差表现如何。
Fixed_reml2 <- lme(fixed = gcse ~ lrt + schgend, random = ~ lrt | school, data = gcse_selected, method="REML") # for extracting standardized level 2 error
gcse_selected$ehat <- residuals(Fixed_reml2, level = 1, type = "normalized")
with(gcse_selected, epiDisplay::summ(ehat, graph = FALSE))## obs. mean median s.d. min. max.
## 4059 0 0.033 0.989 -3.831 3.419## 48 48
## -0.78006114 0.04682792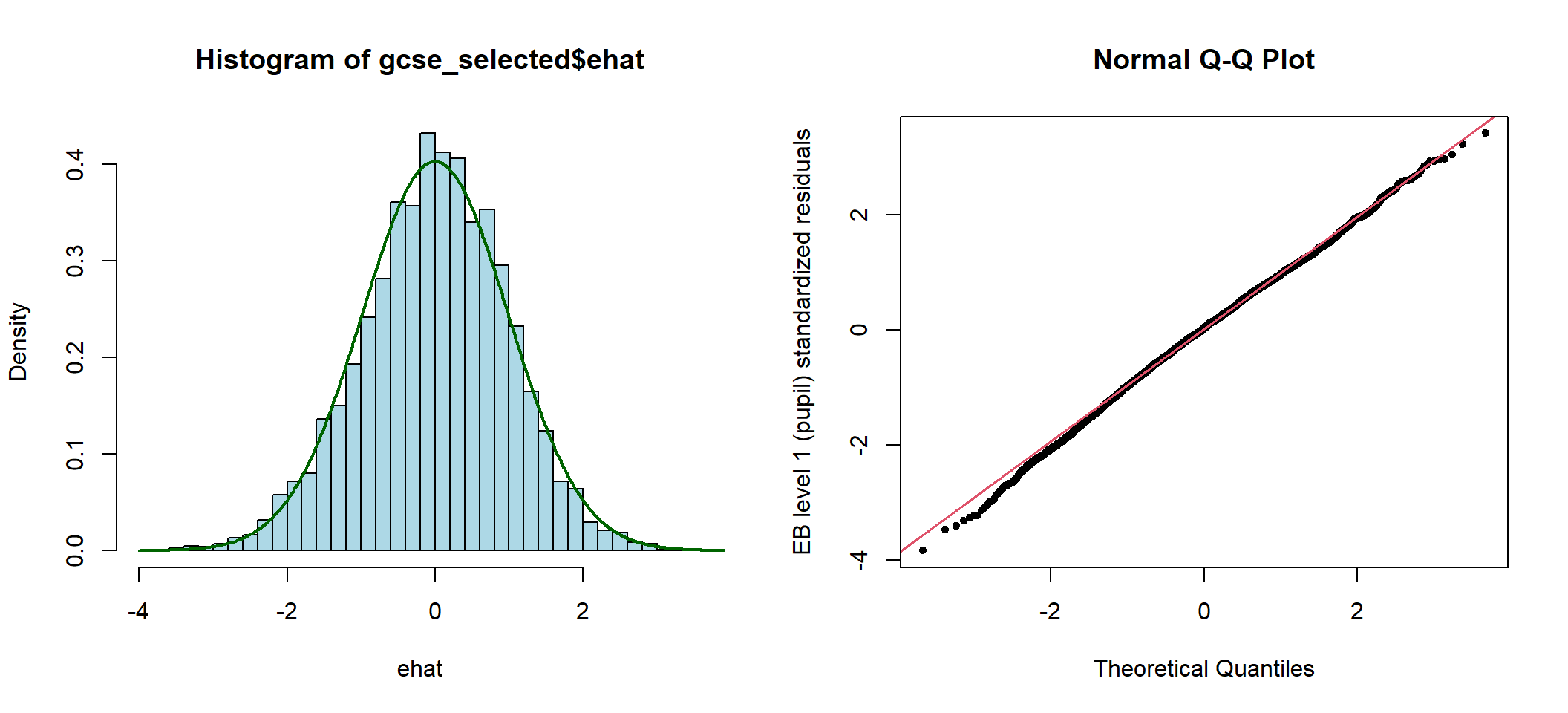
图 49.8: Histogram and Q-Q plots of elementary level (pupil) standardized residuals