第 26 章 多元模型分析
简单线性回归描述的是一个连续型的因变量 \((y)\),和一个单一的预测变量 \((x)\) 之间的关系。我们考虑把这个模型扩展成包含多个预测变量,单一因变量的模型。例如,我们可以考虑建立一个模型使用生活习惯 (包括“年龄,性别,运动,饮食习惯等”) 来预测收缩期血压。此时多重回归的思想就可以帮我们理解一些我们更加关心的因子,与因变量之间的关系,同时控制或者叫调整了其他的混杂因子 (control or adjust confounders) 。有时候这样的模型也可以直接应用到生活中去,比如上面的例子,我们可以通过了解一个人的生活习惯,用建立好的模型来估计这个人的收缩期血压。
建立模型之前,必须明确研究的目的是什么。例如我们关心一个新发现的因子可能与高血压有关系,那么模型中我们放进去调整的其他因子(如年龄,性别,运动) 等和因变量(血压) 之间的关系就变得不那么重要。
多重线性回归,或者叫多元模型分析 (multiple linear regression or multivariable linear regression) 是研究一个连续型因变量和多个预测变量之间关系的重要模型。本章还会着重讨论混杂 (confounding)的概念。
26.1 两个预测变量的线性回归模型
26.1.1 数学标记法和解释
这里假设我们研究一个因变量 \(Y\),和两个预测变量 \((X_1,X_2)\) 的模型。那么此时两个预测变量的线性回归模型可以记为:
\[ \begin{equation} y_i = \alpha + \beta_1 x_{1i} + \beta_2 x_{2i} + \varepsilon_i, \text{ where } \varepsilon_i \sim \text {NID}(0, \sigma^2) \end{equation} \tag{26.1} \]
其中,
- \(y_i\) 是第 \(i\) 名研究对象的因变量数据 (例如体重);
- \(x_{1i}\) 是第 \(i\) 名研究对象的第一个预测变量数据 (例如年龄), \(X_1\);
- \(x_{2i}\) 是第 \(i\) 名研究对象的第二个预测变量数据 (例如身高), \(X_1\);
- \(\alpha\) 的涵义是,当两个预测变量均为 \(0\) 时,因变量的期望值;
- \(\beta_1\) 的涵义是,当 \(X_2\) 不变时,\(X_1\) 每升高一个单位,因变量的期望值;
- \(\beta_2\) 的涵义是,当 \(X_1\) 不变时,\(X_2\) 每升高一个单位,因变量的期望值。
\(\beta_1, \beta_2\) 叫做偏回归系数 (partial regression coefficient)。它们测量的是两个预测变量中,当一个被控制 (保持不变) 时,另一个对因变量的影响。
这个模型也可以用矩阵的形式来表示:
\[ \begin{equation} \textbf{Y} = \textbf{X}\beta+\varepsilon, \text{ where } \varepsilon \sim N(0, \textbf{I}\sigma^2) \\ \left( \begin{array}{c} y_1\\ y_2\\ \vdots\\ y_n \end{array} \right) = \left( \begin{array}{c} 1& x_{11} & x_{21} \\ 1& x_{12} & x_{22} \\ \vdots & \vdots& \vdots \\ 1& x_{1n}& x_{2n} \\ \end{array} \right)\left( \begin{array}{c} \alpha \\ \beta_1\\ \beta_2 \end{array} \right)+\left( \begin{array}{c} \varepsilon_1\\ \varepsilon_2\\ \vdots\\ \varepsilon_n\\ \end{array} \right) \end{equation} \tag{26.2} \]
此时上面的表达式中,\(\textbf{X}\) 是一个矩阵,\(\textbf{Y, \beta, \varepsilon}\) 均为向量。残差被认为服从多变量正态分布(Multivariate normal distribution) ,这个多变量正态分布的协方差矩阵为\(\sigma^2\) 和单位矩阵\(\textbf{I}\) 的乘积来描述。这等价于假设残差是独立同分布且方差 \(\sigma^2\) 不变。
26.1.2 最小平方和估计
跟简单线性回归相似地,我们需要通过对残差平方和最小化,来获得此时多重线性回归的各项参数估计:
\[ \begin{equation} SS_{RES} = \sum_{i=1}^n \hat\varepsilon_{i}^2 = \sum_{i=1}^n(y_i-\hat{y})^2=\sum_{i= 1}^n(y_i-\hat\alpha-\hat\beta_1x_{1i}-\hat\beta_2x_{2i})^2 \end{equation} \tag{26.3} \]
求能让这个残差平方和取最小值的参数估计 \(\hat\alpha,\hat\beta_1,\hat\beta_2\) 我们会在下一章用矩阵标记法来解释。此处要强调的是,这些估计量都是无偏估计量,且可以被证明的是残差方差可以用下面的式子来定义:
\[ \begin{equation} \hat\sigma^2=\sum_{i=1}^n\frac{\hat\varepsilon_i^2}{(n-3)}=\frac{\sum_{i=1}^n(y_i-\ hat\alpha-\hat\beta_1x_{1i}-\hat\beta_2x_{2i})^2}{(n-3)} \end{equation} \tag{26.4} \]
26.2 线性回归模型中使用分组变量
之前我们已展示过,分组变量可以使用哑变量来表示。分组变量多于两组时,可用多个哑变量来同时表示。现在假设变量 \(X\) 有三个分组分别用 \(1,2,3\) 来表示。那么用哑变量来描述含有这个分组变量的数学方法可以标记为:
\[ \begin{equation} y_i = \alpha+\beta_1u_{1i}+\beta_2u_{2i}+\varepsilon_i, \text{ where } \varepsilon_i \sim \text{NID} (0,\sigma^2) \end{equation} \tag{26.5} \]
其中
\[ \begin{aligned} u_{1i}=\left\{ \begin{array}{ll} 1 \text{ if } x_i=2 \\ 0 \text{ if } x_i\neq2 \\ \end{array} \right. ; u_{2i}=\left\{ \begin{array}{ll} 1 \text{ if } x_i=3 \\ 0 \text{ if } x_i\neq3 \\ \end{array} \right. \end{aligned} \]
其实如果你愿意,你也可以把公式 (26.5) 写成下面这样:
\[ \begin{aligned} \begin{array}{ll} y_i = \alpha + \varepsilon_i & \text{if } x_i=1 \\ y_i = \alpha +\beta_1+ \varepsilon_i & \text{if } x_i=2 \\ y_i = \alpha +\beta_2+ \varepsilon_i & \text{if } x_i=3 \\ \end{array} \end{aligned} \] 所以,
- \(\alpha\) 是 \(X=1\) 时因变量的期待值;
- \(\alpha+\beta_1\) 是 \(X=2\) 时因变量的期待值,所以 \(\beta_1\) 是分组变量 \(X\) 前两组之间因变量的期待值的差;
- \(\alpha+\beta_2\) 是 \(X=3\) 时因变量的期待值,所以 \(\beta_2\) 是分组变量 \(X\) 前两组之间因变量的期待值的差。
此时的 \(X=1\) 这个组通常被当作是分组变量中的基准组,也就是参照组 (reference group)。实际情况下你可能可以改变这个参照组为其他组的任意一个。
26.3 协方差分析模型
协方差分析模型用来分析一个连续型的因变量\(Y\) ,与一个连续型的预测变量\((X_1)\)和一个二分类的预测变量\((X_2= 1,2)\),模型被标记为:
\[ \begin{equation} y_i=\alpha+\beta_1x_{1i}+\beta_2u_{2i}+\varepsilon_i, \text{ where } \varepsilon_i \sim \text{NID}(0,\sigma^2) \end{equation} \tag{26.6} \] 其中,
- \(y_{i}\) 为第 \(i\) 名研究对象的因变量数据 (连续型);
- \(x_{1i}\) 为第 \(i\) 名研究对象的第一个预测变量 (也是连续型);
- \(u_i =\left\{ \begin{array}{ll} 1 \text{ if } x_{2i}=2 \\ 0 \text{ if } x_{2i}=1 \\ \end{array}\right.\)
此模型中用到的参数有:
- \(\alpha\) 是截距,意为当 \(X_1=0\) 且 \(X_2=1 \; (u=0)\) 时的因变量期待值;
- \(\beta_1\) 是当 \(X_2\) 保持不变时,\(X_1\) 每升高一个单位时,因变量 \(Y\) 的期待值;
- \(\beta_2\) 是当 \(X_1\) 保持不变时,分组变量 \(X_2\) 的两组之间因变量 \(Y\) 的期待值差异大小。
所以理解了上面的解释之后,就可以将表达式 (26.6) 描述为:
\[ \begin{array}{ll} y_i=\alpha+\beta_1x_{1i}+\varepsilon_i & \text{ if } x_{2i}=1 \\ y_i=\alpha+\beta_2+\beta_1x_{1i}+\varepsilon_i & \text{ if } x_{2i} = 2 \end{array} \]
所以,在一个二维图形中绘制这两条回归直线,你会发现他们之间是平行的。因为他们之间相差的只有截距,决定直线斜率的回归系数,都是 \(\beta_1\)。再用之前用过的数据,儿童的体重和年龄,如果此时考虑了性别因素的话,多重线性回归的输出结果和图形分别应该是:
growgam1 <- read_dta("../Datas/growgam1.dta")
growgam1$sex <- as.factor(growgam1$sex)
Model1 <- lm(wt ~ age + sex, data=growgam1)
print(summary(Model1), digits = 5)##
## Call:
## lm(formula = wt ~ age + sex, data = growgam1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.19236 -0.76268 -0.00696 0.75675 3.79163
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.152414 0.234254 30.5327 < 2.2e-16 ***
## age 0.163998 0.010919 15.0189 < 2.2e-16 ***
## sex2 -0.518854 0.183053 -2.8344 0.005095 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.2503 on 187 degrees of freedom
## Multiple R-squared: 0.5597, Adjusted R-squared: 0.55499
## F-statistic: 118.85 on 2 and 187 DF, p-value: < 2.22e-16## Analysis of Variance Table
##
## Response: wt
## Df Sum Sq Mean Sq F value Pr(>F)
## age 1 359.06 359.06 229.6755 < 2.2e-16 ***
## sex 1 12.56 12.56 8.0341 0.005095 **
## Residuals 187 292.35 1.56
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1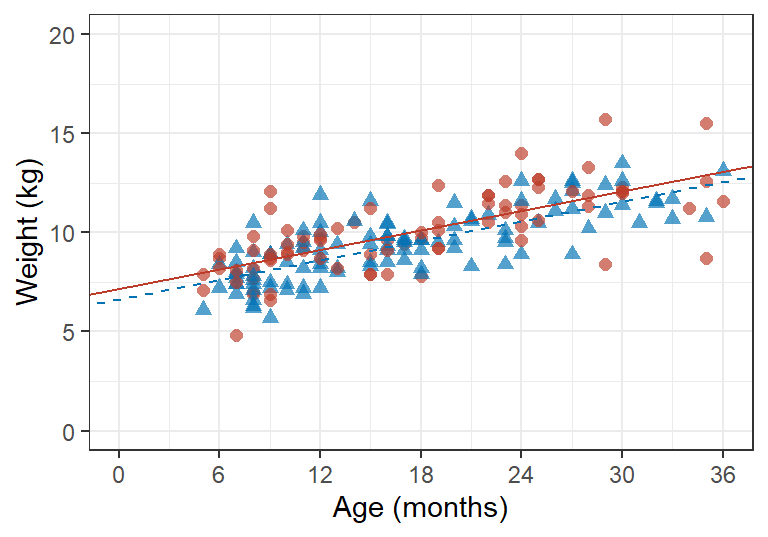
图 26.1: Data and fitted values from a regression model relating age and gender to data from a cross-sectional survey. For male children data points shown as circles and fitted values linked by a solid line. For female children data points shown as triangles and fitted values linked by a dashed line.
26.4 偏回归系数的变化
在增加不同的预测变量进入线性回归模型中时,原先在方程中的预测变量的偏回归系数发生了怎样的变化?
我们先从最简单的开始入手。先只考虑一个简单先行回归模型的情况。当我们新加入一个预测变量,模型发生了什么变化?
\[ \begin{aligned} & \text{Model 1: } y_i = \alpha^*+\beta_1^*x_{1i}+\varepsilon^*_i \\ & \text{Model 2: } y_i = \alpha + \beta_1x_{1i} + \beta_2 x_{2i}+\varepsilon_i \end{aligned} \] \(\beta_1, \beta_1^*\) 表示的其实是完全不同的含义。 \(\beta_1^*\) 被称为粗回归系数 (crude coefficient),或者叫做调整前回归系数,\(\beta_1\) 被称为调整后回归系数 (adjusted coefficient)。二者之间的差异,其实是可以通过对这两个变量进行简单线性回归来度量的:
\[ \text{Model 3: } x_{2i} = \gamma+\delta_1x_{1i}+\omega_i \] 将 Model 2 中的 \(x_{2i}\) 用 Model 3 来替换掉: \[ \begin{aligned} \text{Model 2: }y_i &= \alpha + \beta_1 x_{1i} + \beta_2(\gamma + \delta_1x_{1i}+\omega_i) +\varepsilon_i \\ &= \alpha + \beta_2\gamma+(\beta_1+\beta_2\delta_1)x_{1i}+\beta_2\omega_i + \varepsilon_i \end{aligned} \] 比较 Model 1 和变形过后的 Model 2 中 \(x_{1i}\) 的系数就不难发现:
\[ \beta_1^* = \beta_1 + \beta_2\delta_1 \] 由此可见,调整前后 \(x_{1i}\) 的回归系数的变化 \(\beta_1^*, \beta_1\) 之间的差异,取决于两个部分的大小:
- \(\beta_2\) 的大小和它的符号;
- \(X_1, X_2\) 这两个预测变量之间有多大关联,用 Model 3 的 \(\delta_1\) 来度量。
所以,当调整后的 \(\beta_1 > 0\) 时,要分三种情况来讨论
26.4.1 情况1: \(\beta_1 > \beta_1^*\)
此时,\(\beta_2\delta_1<0\) 所以,二者之间一正一负。如下图所示:
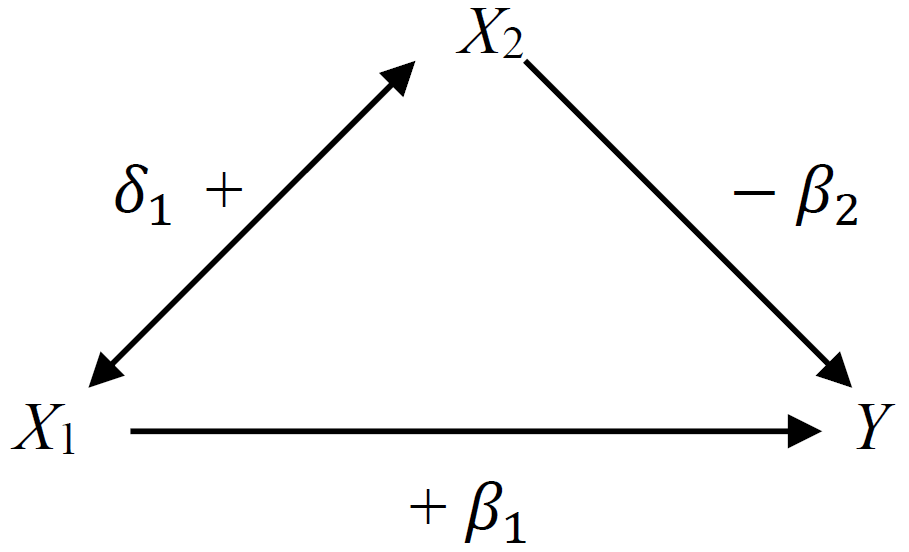
按图所示,当 \(X_2\) 保持不变,\(X_1\) 与因变量 \(Y\) 正相关 (\(\beta_1>0\))。但是,两个预测变量之间 \(X_1, X_2\) 也呈正相关关系 \(\delta_1 >0\)。而同时,\(X_2\) 的升高会导致因变量 \(Y\) 的下降 ($_2 <0 \()。这种情况就意味着,如果,我们不调整\)X_2$ (使之保持不变),那么\(X_1\) 每升高一个单位,\(Y\) 的变化会低于调整\(X_2\) 时,\(X_1\) 的变化所引起的\(Y\) 的变化。如果这时候\(\beta_2,\delta_1\) 较大,那么对于\(X_1\) 来说,调整\(X_2\) 前后,回归系数的变化较大,如果大到一定程度,甚至调整前后的回归系数的方向(正负) 都会发生变化。
26.4.2 情况2:\(\beta_1<\beta_1^*\)
本情况下,\(\beta_2\delta_1>0\) 是正的。所以二者要么同时为正,要么同时为负。如下图所示:
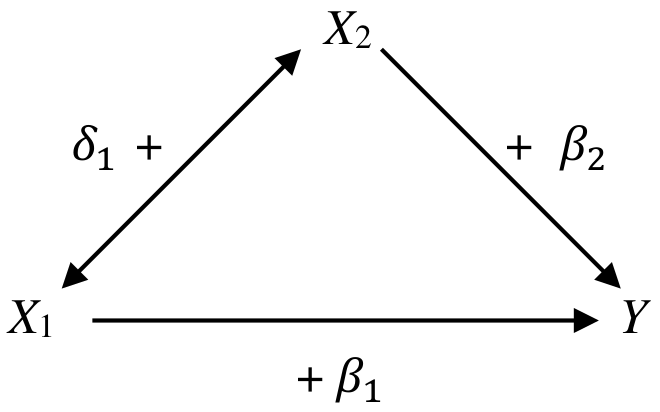
当 \(X_2\) 保持不变时, \(X_1\) 同 \(Y\) 呈正关系。但是,\(X_1\) 的升高也会引起 \(X_2\) 的升高,同时通过 \(X_2\) 和 \(Y\) 之间的正关系升高 \(Y\)。所以假设在模型里我们不对 \(X_2\) 进行控制 (controld or adjust),那么 \(X_1\) 和 \(Y\) 之间的关系就被夸大了。
所以,当 \(X_1\rightarrow X_2\rightarrow Y\) 的这条通路大大超过 \(X_1\rightarrow Y\) 的话,调整后的回归系数 \(\beta_1\) 就会变得很小。
26.5 混杂
流行病学家最喜欢的词汇恐怕要属混杂(confounding) 了(interaction, 交互作用也要算一个(Section 29,(笑))。他们常用混杂来解释为什么调整其他因子前后回归系数发生了变化。当有其他因子(测量了或者甚至是未知的) 对我们关心的预测变量和因变量之间的关系产生了影响(加强或是减弱) 时,就叫做发生了混杂。
对于一个预测变量是否够格被叫做混杂因子,它必须满足下面的条件:
- 与关心的预测变量相关 (i.e. \(\delta_1 \neq 0\));
- 与因变量相关 (当关心的预测变量不变时,\(\beta_2\neq0\) );
- 不在预测变量和因变量的因果关系 (如果有的话) 中作媒介。 Not be on the causal pathway between the predictor of interest and the dependent variable.
有时,判断一个因子是否对我们关心的预测变量和因变量之间的关系构成了混杂并不容易,也不直观。所以,有太多太多的情况下,我们无法准确地 100% 地确定我们关心的关系是否被别的因子混杂。所以,莫要用 “混杂” 一词简单糊弄人。
26.5.1 作为媒介
多数情况下,我们也无法从数据判断一个变量是否在我们关心的预测变量和因变量之间关系的通路上。此时要做的是离开你的电脑,去学习他们之间的生物学知识,看是否真的有关系。
但是有些例子就很简单啦。比如说,服用降血压药物可以预防发生中风。那么此时血压的降低,就处在了这二者因果关系的通路上。因为药物通过降低了血压,从而预防了中风的发生。这一关系中,我们不能说血压是混杂因子,它是一个媒介 (mediator)。但是多数的横断面研究 (cross-sectional study) 中我们无法是很难下结论的。
