第 18 章 置信区间

18.1 定义

置信区间的定义，曾经在统计推断中介绍过 (Section 10.1)。置信区间 (CI)，提供了一种对参数估计精确度的度量。 CI，也是一种统计量，有自己的样本分布，它总是成对成对地出现的。 L，表示下限，U，表示上限。显著性水平 (confidence level) 下的下限和上限之间的间距大小，是由置信区间本身的样本分布决定的。

一般地，对于一个总体参数 \(\mu\)，它的 \(100(1-\alpha)\%\text{CI}\) 置信区间的含义为：

\[ \begin{equation} \text{Prob}\{\mu\in (\text{L}, \text{U}) | \mu\} = (1-\alpha) \end{equation} \tag{18.1} \]

所以，一个总体参数 \(\mu\)，的 \(95\%\text{CI}\) 置信区间为：

\[ \begin{equation} \text{Prob}\{ \mu \in (\text{L, U}) | \mu\} =0.95 \end{equation} \tag{18.2} \]

用公式 (18.2) 来解释就是，区间 \(\text{(L, U)}\) 内包含了总体参数 \(\mu\) 的概率为 \(95\%\)。本文以下部分从公式中省略 \(|\mu\) 部分。但是必须要记住，概率论环境下的置信区间 (或者其他统计学参数估计) 都是总体参数的条件概率。在概率论语境下，置信区间一般是左右对称的。所以 \(100(1-\alpha)\%\text{CI}\) 的含义可以解读为：

\[ \begin{equation} \text{Prob} \{ \mu \leqslant \text{L} \} = \text{Prob} \{ \mu \geqslant \text{U} \} = \frac{\alpha}{2} \end{equation} \tag{18.3} \]

General definition of a CI for a 95% CI

图 18.1: General definition of a CI for a 95% CI

18.2 利用总体参数的样本分布求置信区间

总体参数的样本分布是求其置信区间的关键。假设 \(\hat\mu\) 是总体参数 \(\mu\) 的估计量。且已知存在两个单调递增函数 \(A(\mu), B(\mu)\) 来描述该总体参数 \(\mu\) ：

\[ \begin{equation} \text{Prob} \{ \hat\mu \leqslant A(\mu) \} = \text{Prob} \{ \hat\mu \geqslant B(\mu) \} = \frac{\alpha}{2 } \end{equation} \tag{18.4} \]

所以，

\[ \begin{equation} \text{Prob} \{ A^{-1} (\hat\mu) \leqslant \mu \} = \text{Prob} \{ B^{-1}(\hat\mu) \geqslant \mu \} = \frac{\alpha}{2} \end{equation} \tag{18.5} \]

因此，\(A^{-1}(\hat\mu), B^{-1}(\hat\mu)\) 就是我们想要找的公式(18.3) 参数的估计置信区间的下限\(\text{L}\)，和上限\(\text{U}\)。所以，关键的任务就在于，每一次寻找计算参数样本分布的方程 \(A, B\) 。

18.3 情况1：已知方差的正态分布数据均值的置信区间

从已知正态分布且方差为\(\sigma^2\) 的人群中抽取样本量为\(n\) 的相互独立观察数据\(Y_i (i=1,2,\cdots,n)\) 。该样本均值的估计量 \(\hat\mu=\bar{Y}\)，也服从方差已知的 \((\frac{\sigma^2}{n})\) 正态分布：

\[ \begin{equation} \bar{Y}\sim N(\mu, \frac{\sigma^2}{n}) \Leftrightarrow Z=\frac{\bar{Y}-\mu}{\sqrt{\frac{\sigma^ 2}{n}}} \sim N(0,1) \end{equation} \tag{18.6} \]

所以利用标准正态分布，往公式(18.3) 尽可能靠：\(\text{Prob}\{ Z \leqslant z_{\alpha/2}\} = \text{Prob}\{ Z \geqslant z_{1-\alpha/2}\} = \frac{\alpha}{2}\) 。

把式子 (18.6) 代入以后：

\[ \begin{equation} \text{Prob}\{ \bar{Y} \leqslant \mu+z_{\alpha/2}\frac{\alpha}{\sqrt{n}} \} = \text{Prob}\{ \bar{ Y} \geqslant \mu+z_{1-\alpha/2}\frac{\alpha}{\sqrt{n}} \} = \frac{\alpha}{2} \end{equation} \tag{18.7} \]

至此，我们找到了描述总体均值的单调函数：

\[ \begin{aligned} A(\mu) &= \mu + z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \\ B(\mu) &= \mu + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} \end{aligned} \]

由于标准正态分布左右对称，所以\(z_{\alpha/2}=-z_{1-\alpha/2}\) ，因而，\(A(\mu) = \mu - z_{1-\alpha/2 }\frac{\sigma}{n}\)。

此时，求置信区间上限和下限的方法应该已经一目了然：

\[ \begin{equation} \text{U} =A^{-1}(\bar{Y})=\bar{Y} + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} \\ \text{L} = B^{-1}(\bar{Y})=\bar{Y} - z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} \end{equation} \tag{18.8} \]

我们也常将它简写成为：\(\text{CI} = \bar{Y} \pm z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\)。

它的意义是：

\[ \begin{equation} \text{Prob} \{ \bar{Y} - z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \bar{Y} + z_{1-\ alpha/2}\frac{\sigma}{\sqrt{n}} \} = 1-\alpha \end{equation} \tag{18.9} \]

所以区间\((\bar{Y} - z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}, \bar{Y} + z_{1-\alpha/2}\frac {\sigma}{\sqrt{n}})\) 包含了总体参数均值\((\mu)\) 的概率是\(1-\alpha\)。我们把这个区间叫做总体均值 \(\mu\) 的 \(100(1-\alpha)\%\) 置信区间。常说的 \(95\%\) 置信区间我们使用的 \(z_{0.975} = 1.96\)。其他置信水平的 \(z\) 值举例如下：

\[ \begin{array}{lr} z_{0.90} = 1.28 & \text{for } 80\% \text{ level} \\ z_{0.95} = 1.645 & \text{for } 90\% \text{ level} \\ z_{0.995} = 2.58 & \text{for } 99\% \text{ level} \\ z_{0.9995} = 3.29 & \text{for } 99.9\% \text{ level} \\ \end{array} \]

所以，根据上面罗列的不同置信水平下\(z\) 值的大小，我们不难判断\(\text{CI} = \bar{Y} - z_{1-\alpha/2}\frac{\sigma}{ \sqrt{n}}\) 范围随着标准差增大而变宽(不精确)，随着样本量增加而变窄(精确)。

这里补充另一个容易混淆的概念，参数估计的置信区间公式\(\text{CI} = \bar{Y} \pm z_{1-\alpha/2}\frac{\sigma}{\sqrt{n} }\) ，和参考值范围(reference range) 是不同的概念。后者的公式为 \(\bar{Y}\pm z_{1-\alpha/2} \sigma\)。参考值范围的意义是， \(95\%\) 的样本数据包含在这个区间内。置信区间，给出的是这个样本对总体均值的估计的精确度。

18.4 置信区间的意义

当\(\alpha = 0.05\) 时，我们说\((\bar{Y} - z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}, \bar{Y} + z_{ 1-\alpha/2}\frac{\sigma}{\sqrt{n}})\) 包含了总体参数均值\((\mu)\) 的概率是\(95\%\)。但是要记住，千万不能说：总体参数 \(\mu\) 有 \(95\%\) 的概率落在这个置信区间内。因为总体参数不是随机变量，它不会随我们的样本变化而变化，它是恒定不变的。我们每一次实验，每一次采样，获得的样本数据，计算出一个新的置信区间，这样的区间都是在估计这个未知位置的总体参数。所以，从长远来说，相同的实验，重复20次，其中19次计算获得的置信区间，会包含真实的总体参数。

18.5 情况2：未知方差，但是已知服从正态分布数据均值的置信区间

多数情况下，总体的方差我们无从知晓。它也必须通过实验数据来估计 \(\hat\sigma^2\)。那么，下面的公式计算的统计量 \(T\) 服从自由度为 \(n-1\) 的 \(t\) 分布：

\[ T=\frac{\bar{Y}-\mu}{\sqrt{\hat\sigma^2/n}} \sim t_{n-1} \]

用跟前面类似的办法，用统计量 \(T\) 取代 \(Z\)，我们可以求未知方差时正态分布数据均值的置信区间 (类比 (18.8))：

\[ \begin{aligned} &\text{U} = \bar{Y} + t_{n-1, 1-\alpha/2}\frac{\sigma}{\sqrt{n}} \\ &\text{L} = \bar{Y} - z_{n-1, 1-\alpha/2}\frac{\sigma}{\sqrt{n}} \\ &\text{Or, equivalently :} \\ &\text{CI } = \bar{Y} \pm t_{n-1, 1-\alpha/2}\frac{\sigma}{\sqrt{n}} \end{aligned} \tag{18.10} \]

18.6 情况3：服从正态分布的随机变量方差的置信区间

用 \(Y_i (i=1,2,\cdots,n)\) 标记样本量为 \(n\) 的独立观察数据。已知该数据来自的人群服从正态分布，但是方差未知。那么从统计推断第二章 (Section 10.4) 推导过的内容，我们知道：

\[ \begin{aligned} &\text{Sample variance is defined as: } \\ &\hat\sigma^2 = \frac{\sum_{i=1}^n(Y_i-\bar{Y})^2}{n-1} \\ &\text{and } \\ &\frac{(n-1)\hat\sigma^2}{\sigma^2} \sim \chi^2_{n-1} \\ &\text{It follows that we want } \\ &\text{Prob}\{ \hat\sigma^2 \leqslant \frac{\sigma^2}{n-1}\chi^2_{n-1, \alpha/2} \} = \text{Prob }\{ \hat\sigma^2 \geqslant \frac{\sigma^2}{n-1}\chi^2_{n-1, 1-\alpha/2} \} = \frac{\alpha}{ 2} \\ & \Rightarrow \text{U} = \frac{(n-1)\hat\sigma^2}{\chi^2_{n-1, \alpha/2}} \; \text{L} = \frac {(n-1)\hat\sigma^2}{\chi^2_{n-1, 1-\alpha/2}} \\ \end{aligned} \]

当样本量足够大时，根据中心极限定理，当样本量足够大时，样本均数服从正态分布，即使样本数据并不服从正态分布。这就意味着，样本足够大，章节 18.4 中用到的均值置信区间公式，也可适用于样本数据不服从正态分布的情况下。我们常使用这个定理，和章节18.4 中的公式去计算许多总体均数以外的参数的\(95\%\) 置信区间，通过正态分布近似法计算获得的置信区间，被叫做近似置信区间。

18.7 情况4：求人群百分比的置信区间

18.7.1 一般原则

用 \(R\) 表示 \(n\) 次实验中成功的次数。如果满足实验相互独立的条件，那么 \(R\sim \text{Binomial}(n,\pi)\)。那么样本比例 \(P=\frac{R}{n}\) 是人群比例 \(\pi\) 的无偏估计。如果想要求 \(\pi\) 的 \(95\%\) 置信区间 \((\pi_L, \pi_U)\)，我们可能自然而让想到用成功次数 \(R\) 来计算。然而，由于 \(R\) 本身是离散型变量 (只能取大于等于零的整数)，恰好加起来概率等于 \(95\%\) 的 \(\pi\) 的区间是几乎不可能计算的。我们处理比例的置信区间的问题时，要计算的两个下限值和上限值要满足的条件：

  1. 寻找最小的 \(\pi_L\) 满足 \(\text{Prob}(\pi_L>\pi) \leqslant 0.025\)
  2. 寻找最大的 \(\pi_U\) 满足 \(\text{Prob}(\pi_U<\pi) \leqslant 0.025\)

有两种方案可供选择：

  1. 利用样本分布服从二项分布 \(R \sim \text{Binomial}(n, \pi)\) 的原则来“精确”计算；
  2. 正态近似法计算。

第一种方法被叫做精确法，并不是因为它能够精确计算恰好概率和等于 \(95\%\) 的所有的 \(\pi\)，而是因为它利用的是样本分布的二项分布属性进行计算。然而随着样本量的增加，两种方法计算的置信区间结果越来越接近概率和 \(95\%\)。

18.7.2 二项分布的“精确法”计算置信区间

例：样本量 \(n=20\), 成功次数 \(r=5\) 时，你可以用查水表的办法，也可以利用 R 进行精确计算

binom.test(5, 20, conf.level = 0.95)
## 
##  Exact binomial test
## 
## data:  5 and 20
## number of successes = 5, number of trials = 20, p-value = 0.04139
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
##  0.08657147 0.49104587
## sample estimates:
## probability of success 
##                   0.25

下面两个图分别展示了当 \(\pi\) 等于精确法计算的下限和上限时的概率分布。可以看出 \(\pi=0.0866\) 时，\(\text{Prob}\{R \geqslant 5\} \leqslant 0.025\)。同时，当 \(\pi = 0.4910\) 时， \(\text{Prob}\{ R\leqslant 5 \} \leqslant 0.025\)

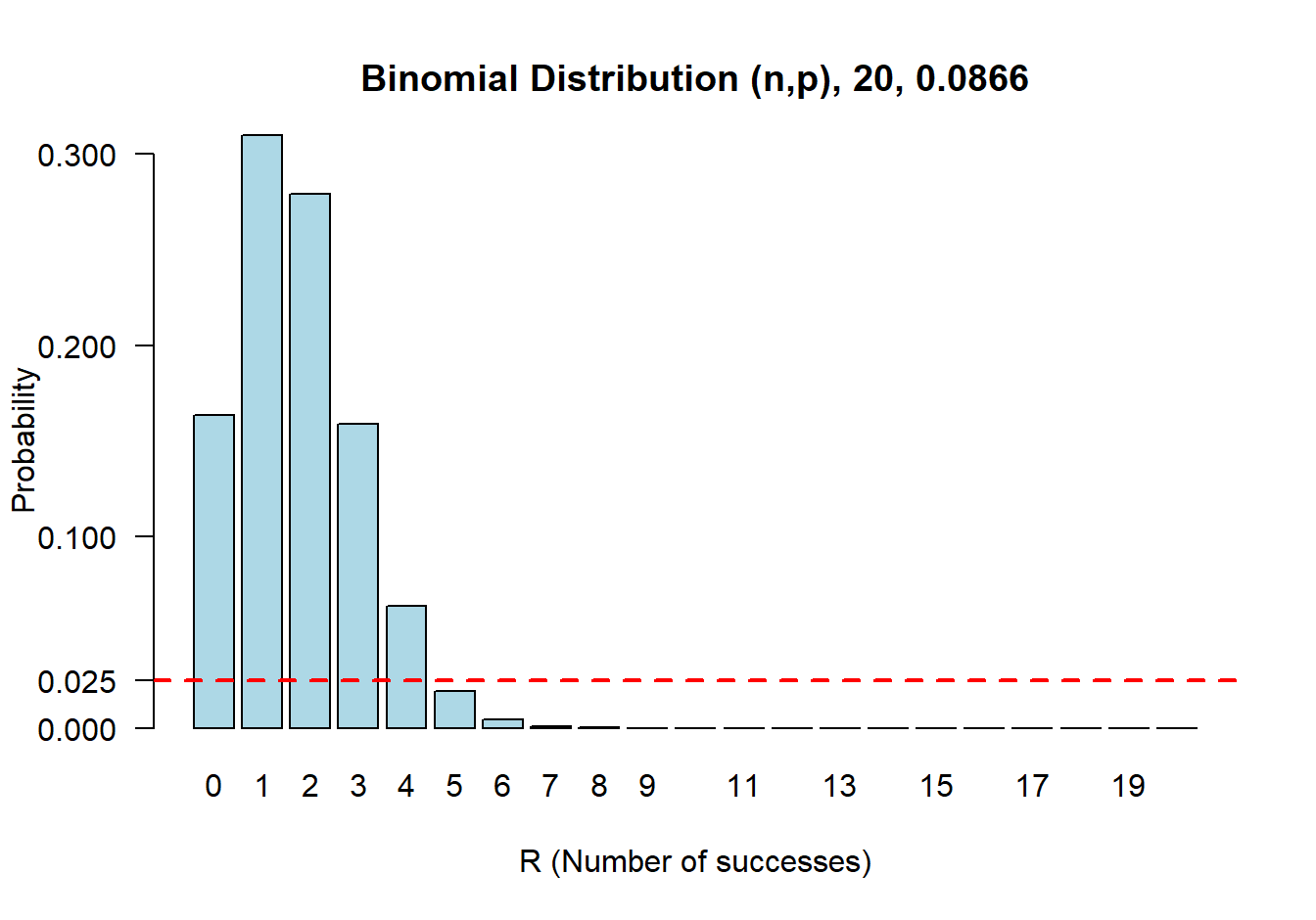
Sampling distribution of number of successes out of 20 (R) conditional on the probability of success being 0.0866

图 18.2: Sampling distribution of number of successes out of 20 (R) conditional on the probability of success being 0.0866

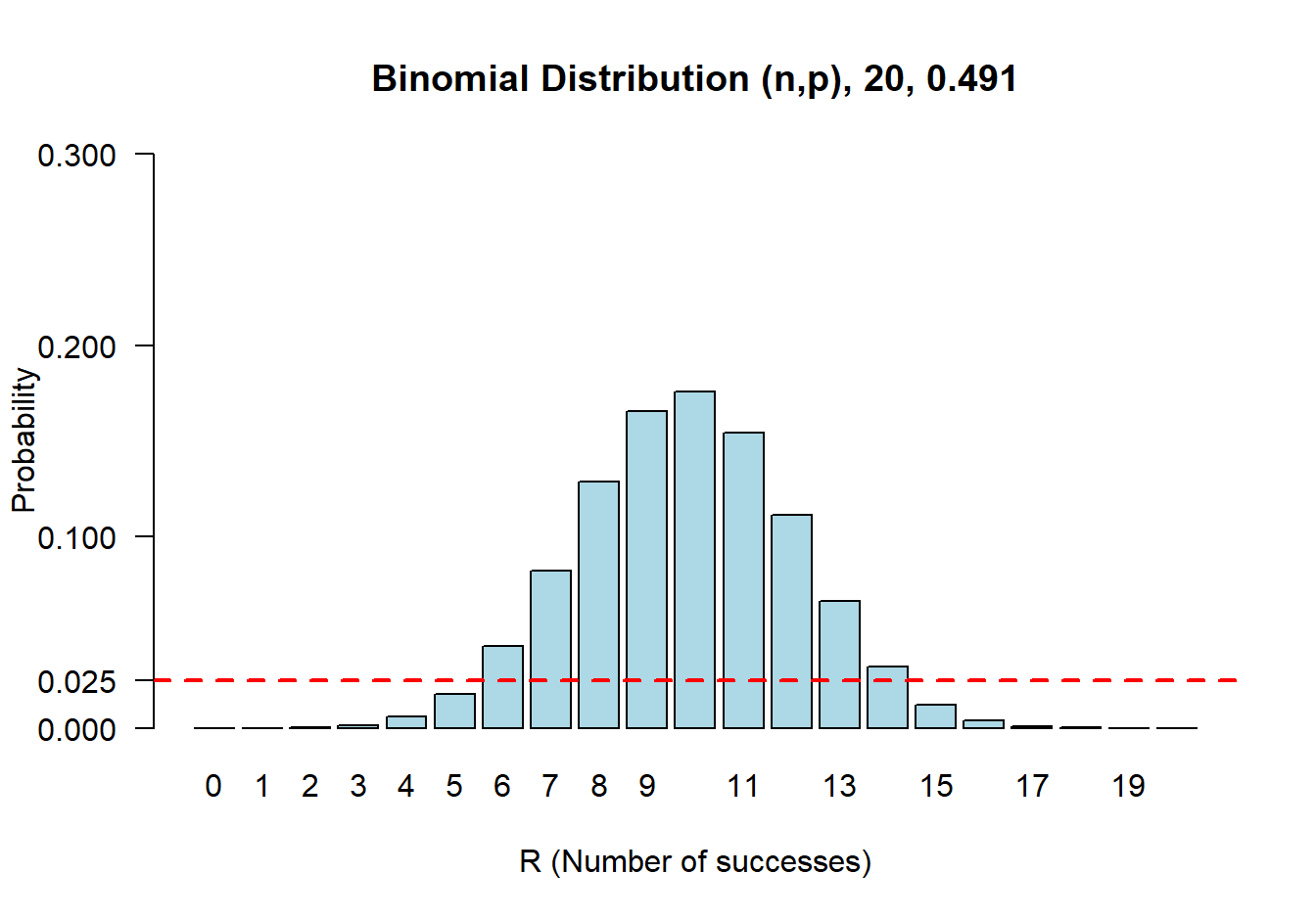
Sampling distribution of number of successes out of 20 (R) conditional on the probability of success being 0.4910

图 18.3: Sampling distribution of number of successes out of 20 (R) conditional on the probability of success being 0.4910

18.7.3 二项分布的近似法计算置信区间

当 \(n\) 较大时，百分比 \(P\) 分布 可以用正态分布来近似：

\[ P\sim N(\pi, \sigma^2) \text{ where } \sigma^2 = \frac{\pi(1-\pi)}{n} \]

总体均值用样本百分比\(p\) 替代，方差用样本方差\(\hat\sigma^2 = \frac{p(1-p)}{n}\)，因此，当样本量较大时二项分布的近似正态分布特征可以描述为：

\[ P \sim N(p, \hat\sigma^2) \text{ where } \hat\sigma^2 = \frac{p(1-p)}{n} \]

接下去对与百分比的置信区间的计算就可以套用章节 18.4 中用到的均值置信区间公式：

\[ \begin{aligned} & P\pm z_{1-\alpha/2}\sqrt{\frac{P(1-P)}{n}} \\ & \text{ where } z_{1-\alpha/2} = 1.96 \text{ for } 95\% \text{CI} \end{aligned} \tag{18.11} \]

正态近似法的好处是简单，但是代价就是样本量小时不准确。

例如：

  1. \(n=10, r=4, p=0.4\) 时
    • 精确法 \(95\%\) 置信区间：0.1215523, 0.7376219
    • 正态近似法\(95\%\) 置信区间：\(0.4\pm1.96\sqrt{\frac{0.4\times0.6}{10}} =\) 0.0963581, 0.7036419
  2. \(n=50, r=20, p=0.4\) 时
    • 精确法 \(95\%\) 置信区间：0.2640784, 0.548206
    • 正态近似法\(95\%\) 置信区间： \(0.4\pm1.96\sqrt{\frac{0.4\times0.6}{50}} =\) 0.2642072, 0.5357928
  3. \(n=1000, r=400, p=0.4\) 时
    • 精确法 \(95\%\) 置信区间：0.369469, 0.4311216
    • 正态近似法\(95\%\) 置信区间： \(0.4\pm1.96\sqrt{\frac{0.4\times0.6}{1000}} =\) 0.3696358, 0.4303642

可以明显看到随着样本量增加，置信区间本身的范围在不断变小 (精确)。且正态近似法计算的置信区间也越来越接近“精确法”。 “Statistical Methods in Medical Research”(Armitage, Berry, and Matthews 2008) 书中建议，满足\(n\pi \geqslant 10 \text{ or } n(1-\pi) \geqslant 10\) 时，正态近似法可以给出较为满意的百分比的置信区间估计。

18.8 率的置信区间

18.8.1 利用泊松分布精确计算

假设在一段时间 \(t\) 内某事件发生的次数记为 \(Y\)。如果每个相同事件的发生相互独立那么 \(Y \sim \text{Poisson}(\mu t)\)。样本率 \(R=\frac{Y}{t}\)，是人群事件发生概率 \(\mu\) 的无偏估计。

\[ \text{The probability that } Y=y \text{ is given by } \frac{(\mu t)^y e^{-\mu t}}{y!} \text{ for } y= 0,1, 2,\cdots,\infty \]

与前一节百分比的精确计算置信区间相类似 (Section 18.7.2)，我们可以使用泊松分布的性质进行计算：

  1. 寻找最小的 \(\mu_L\) 满足 \(\text{Prob}(\mu_L>\mu) \leqslant 0.025\)
  2. 寻找最大的 \(\mu_U\) 满足 \(\text{Prob}(\mu_U<\mu) \leqslant 0.025\)

例：某核电站附近的村庄从1968年起的10年内，发生了 6 人死于白血病。平均死亡率为 0.6/年。计算死亡率的95%置信区间。

可以利用 R 的精确计算发病率的代码 poission.test 来获得精确法率的置信区间：

poisson.test(6, 10)
## 
##  Exact Poisson test
## 
## data:  6 time base: 10
## number of events = 6, time base = 10, p-value = 0.2657
## alternative hypothesis: true event rate is not equal to 1
## 95 percent confidence interval:
##  0.2201894 1.3059474
## sample estimates:
## event rate 
##        0.6

18.8.2 利用正态近似法计算

当样本量较大时，发生事件次数 \(Y\) 近似服从正态分布，其均值和方差均等于 \(\mu t\) (参考 Section 6 推导)：

\[ Y \sim N(\mu t, \sigma^2) \text{ where } \sigma^2=\mu t \]

所以事件发生率 \(\mu\) 的置信区间公式为 \(\frac{Y\pm 1.96\sqrt{Y}}{t}\)。

Reference

Armitage, Peter, Geoffrey Berry, and John Nigel Scott Matthews. 2008. Statistical Methods in Medical Research. John Wiley & Sons.