第 1 章 概率基本定义和公理
1.1 三个概率公理:
- 对于任意事件 \(A\),它发生的概率 \(P(A)\) 满足这样的不等式: \(0 \leqslant P(A) \leqslant 1\)
- \(P(\Omega)=1\) , \(\Omega\) 是全样本空间 (total sample space)
- 对于互斥(相互独立)的事件\(A_1, A_2, \dots, A_n\) 有如下的等式关系: \(P(A_1\cup A_2 \cup \cdots \cup A_n)=P(A_1)+P (A_2)+\cdots+P(A_n)\)
你是不是觉得上面三条公理都是废话。
我也是这么觉得的。
然而,正是这样显而易见的道理,确是拿来建筑理论的基石,千万不能小看。例如,看下面这个看似也应该成为公理的公式的证明:
\[ P(A_1\cup A_2) = P(A_1) + P(A_2) - P(A_1 \cap A_2) \]
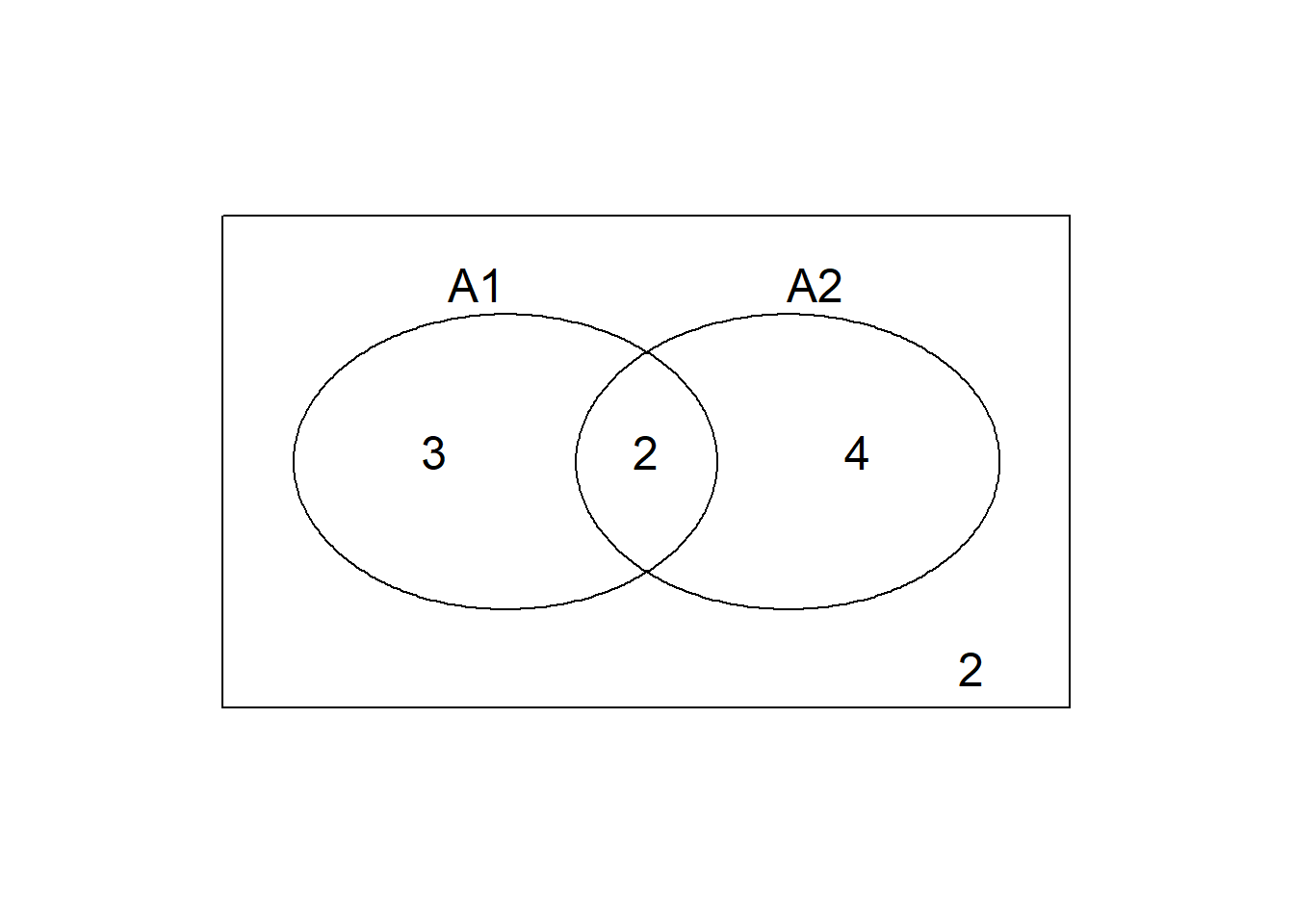
证明:
先考虑 \(A_1 \cup A_2\) 是什么(拆分成三个互斥事件)
\(A_1 \cup A_2 = (A_1\cap \bar{A_2})\cup(\bar{A_1}\cap A_2)\cup(A_1\cap A_2)\)
用上面的公理2,公理3
\(\therefore P(A_1 \cup A_2) = P(A_1\cap \bar{A_2}) + P(\bar{A_1}\cap A_2) + P(A_1\cap A_2) \;\;\;\;\;\;(1)\)
再将 \(A_1=(A_1\cap A_2)\cup(A_1\cap\bar{A_2})\) 继续拆分成两个互斥事件
\(\therefore P(A_1)=P(A_1\cap A_2)+P(A_1\cap\bar{A_2})\) 整理一下:
\(P(A_1\cap\bar{A_2})=P(A_1)-P(A_1\cap A_2)\)
同理可得: \(P(\bar{A_1}\cap A_2)=P(A_2)-P(A_1\cap A_2)\)
代入上面第(1)式可得:
\[ \begin{aligned} P(A_1 \cup A_2) &= P(A_1)-P(A_1\cap A_2)\\ &\;\;+ P(A_2)-P(A_1\cap A_2)\\ &\;\;+P(A_1\cap A_2)\\ &=P(A_1) + P(A_2) - P(A_1 \cap A_2) \end{aligned} \]