第 47 章 随机截距模型 随机截距模型
最简单的随机效应模型 – 随机截距模型 random intercept model。
47.1 随机截距模型的定义
有时,我们对每个分层各自的截距大小并不那么感兴趣,且如果只有固定效应的话,其实我们从某种程度上忽略掉了数据层与层之间变异的方差(between cluster variation )。于是,在模型中考虑这些问题的解决方案就是– 我们让各层的截距呈现随机效应(treat the variation in cluster intercepts not as fixed),把这些截距视为来自与某种分布的随机呈现(randomly draws from some distribution)。于是原先的只有固定效应部分的模型,就增加了随机截距部分:
\[ \begin{aligned} Y_{ij} & = \mu + u_j + \varepsilon_{ij} \\ \text{where } u_j & \stackrel{N.I.D}{\sim} N(0, \sigma_u^2) \\ \varepsilon_{ij} & \stackrel{N.I.D}{\sim} N(0, \sigma_\varepsilon^2) \\ u_j & \text{ are independent from } \varepsilon_{ij} \\ \end{aligned} \tag{47.1} \]
这个混合效应模型中,
- \(\mu\) 是总体均值;
- \(u_j\) 是一个服从均值 0, 方差 (the population between cluster variance) 为 \(\sigma_u^2\) 的正态分布的随机变量;
- \(\varepsilon_{ij}\) 是随机误差,它也被认为服从均值为0, 方差为\(\sigma_\varepsilon^2\) 的正太分布,且这两个随机效应部分之间也是相互独立的。
- 从该模型估算的结果变量 \(Y_{ij}\) 的方差是 \(\sigma_u^2 + \sigma_\varepsilon^2\)。
- 随机截距模型又被叫做是 方差成分模型 (variance-component model),或者是单向随机效应方差模型 (one-way random effects ANOVA model)。
这个模型和仅有固定效应的模型,有显著的不同:
\[ Y_{ij} = \mu + \gamma_j + \varepsilon_{ij} \]
固定效应模型里,
- \(\mu\) 也是总体均值;
- \(\sum_{j=1}^J \gamma_j = 0\) 是将各组不同截距之和强制为零的过程;
所以随机截距模型打破了这个限制,使得随机的截距 \(\mu_j\) 成为一个服从均值为 0,方差为 \(\sigma_u^2\) 的 随机变量。
随机效应部分\(u_j\) 和随机误差\(\varepsilon_{ij}\) 之间相互独立的前提,意味着两个里属于不同层级的观察之间是相互独立的,但是反过来,同属于一个层级的个体之间就变成了有相关性的了(within cluster correlation):
\[ \begin{aligned} \because Y_{1j} & = \mu + u_j + \varepsilon_{1j} \\ Y_{2j} & = \mu + u_j + \varepsilon_{2j} \\ \therefore \text{Cov}(Y_{1j}, Y_{2j}) & = \text{Cov}(u_j, u_j) + \text{Cov}(u_j, \varepsilon_{2j}) + \text{Cov }(\varepsilon_{1j}, u_j) + \text{Cov}(\varepsilon_{1j}, \varepsilon_{2j}) \\ & = \text{Cov}(u_j, u_j) = V(u_j, u_j)\\ & = \sigma_u^2 \end{aligned} \]
由于\(\text{Var}(Y_{1j}) = \text{Var}(Y_{2j}) = \sigma_u^2 + \sigma_\varepsilon^2\),所以,同属一层的两个个体之间的层内相关系数(intra-class correlation):
\[ \lambda = \frac{\text{Cov}(Y_{1j}, Y_{2j})}{\text{SD}(Y_{1j})\text{SD}(Y_{2j})} = \frac {\sigma_u^2}{\sigma_\varepsilon^2 + \sigma_u^2} \]
从层内相关系数的公式也可看出,该相关系数可以同时被理解为结果变量 \(Y_{ij}\) 的方差中归咎与层(cluster)结构的部分的百分比。
This is the within-cluster or intra-class correlation, that we will denote \(\lambda\). Note that it is also the proportion of total variance that is accounted for by the cluster.
47.2 随机截距模型的参数估计
如此,我们就知道在随机截距模型里,有三个需要被估计的参数 \(\mu, \sigma_u^2, \sigma^2_\varepsilon\)。我们可以利用熟悉的极大似然估计法估计这些参数 (Maximum Likelihood, ML)。当且进当嵌套式结构数据是平衡数据 (balanced)时 (即,每层中的个体数量相同),这三个参数的 \(\text{MLE}\) 分别是:
\[ \begin{aligned} \hat\mu & = \bar{Y} \\ \hat\sigma_\varepsilon^2 & = \text{Mean square error, MSE} \\ \hat\sigma_u^2 & = \frac{\text{Model Sum of Squares, MSS}}{Jn} - \frac{\hat\sigma^2_\varepsilon}{n} \end{aligned} \tag{47.2} \]
只要模型指定正确无误,前两个极大似然估计是他们各自的无偏估计。但第三个,也就是层内方差的估计量确实际上是低估了的 (downward biased)。这里常用的另一种对层内方差参数的估计法被叫做矩估计量 (moment estimator, or ANOVA estimator):
\[ \begin{aligned} \widetilde{\sigma}_u^2 & = \frac{\text{MSS}}{(J-1)n}- \frac{\hat\sigma_\varepsilon^2}{n} \\ & = \frac{\text{MSS} - \text{MSE}(J-1)}{(J-1)n} \\ & = \frac{\text{MMS}(J-1) - \text{MSE}(J-1)}{(J-1)n} \\ & = \frac{\text{MMS} - \text{MSE}}{n} \end{aligned} \]
对于平衡数据 (balanced data),这个矩估计量又被叫做限制性极大似然 (Restricted Maximum Likelihood, REML)。限制性极大似然法,是一个真极大似然过程(genuine maximum likelihood procedure),但是它每次进行估计的时候,会先”去除掉”固定效应部分,所以每次用于估计参数的数据其实是对数据的线性转换后\(Y_{ij} - \mu = u_j + \varepsilon_{ij}\),它使用的数据是这个等式右半部分的转换后数据。在 REML 过程中,先估计层内方差 \(\sigma_u^2\) 再对固定效应部分的总体均值估计,所以是个两步走的过程。另外除了这里讨论的ML, REML这两种对层内方差进行参数估计的方法之外,在计量经济学(econometrics) 中常用的是(本课不深入探讨) 广义最小二乘法(Generalized Least Squares, GLS)。 GLS 使用的是一种加权的最小二乘法 (OLS),该加权法根据层与随机误差的方差成分 (variance components) 不同而给不同的层以不同的截距权重。当数据本身是平衡数据时,GLS给出的估计结果等同于 REML法。当数据不是平衡数据的时候,ML/REML 其实背后使用的原理也是 GLS。
47.3 如何在 R 中进行随机截距模型的拟合
在 R 或 STATA 中拟合随机截距模型,需要数据为“长 (long)” 数据,下面的代码可以在 R 里面把 “宽 (wide)” 的数据调整成为 长 数据:
## # A tibble: 6 × 5
## id wp1 wp2 wm1 wm2
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 494 490 512 525
## 2 2 395 397 430 415
## 3 3 516 512 520 508
## 4 4 434 401 428 444
## 5 5 476 470 500 500
## 6 6 557 611 600 625# transform data into long format
pefr_long <- pefr %>%
gather(key, value, -id) %>%
separate(key, into = c("measurement", "occasion"), sep = 2) %>%
arrange(id, occasion) %>%
spread(measurement, value)
pefr_long## # A tibble: 34 × 4
## id occasion wm wp
## <dbl> <chr> <dbl> <dbl>
## 1 1 1 512 494
## 2 1 2 525 490
## 3 2 1 430 395
## 4 2 2 415 397
## 5 3 1 520 516
## 6 3 2 508 512
## 7 4 1 428 434
## 8 4 2 444 401
## 9 5 1 500 476
## 10 5 2 500 470
## # ℹ 24 more rows在 R 里面,有两个包 (lme4::lmer 或 nlme::lme) 的各自两种代码以供选用:
## Linear mixed-effects model fit by REML
## Data: pefr_long
## AIC BIC logLik
## 366.7584 371.248 -180.3792
##
## Random effects:
## Formula: ~1 | id
## (Intercept) Residual
## StdDev: 110.397 19.91084
##
## Fixed effects: wm ~ 1
## Value Std.Error DF t-value p-value
## (Intercept) 453.9118 26.99207 17 16.81649 0
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -2.44443558 -0.33507694 0.03704489 0.35098366 2.37705974
##
## Number of Observations: 34
## Number of Groups: 17## Linear mixed model fit by REML ['lmerMod']
## Formula: wm ~ (1 | id)
## Data: pefr_long
##
## REML criterion at convergence: 360.8
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -2.44444 -0.33508 0.03704 0.35098 2.37706
##
## Random effects:
## Groups Name Variance Std.Dev.
## id (Intercept) 12187.5 110.40
## Residual 396.4 19.91
## Number of obs: 34, groups: id, 17
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 453.91 26.99 16.82不知道为什么在 R 里有这两种完全不同的方式来拟合混合效应模型。还好他们的结果基本完全一致。在这个极为简单的例子里,我们可以利用模型拟合的结果中 Random effects 的部分来计算层内相关系数 (intra-class correlation):
\[ \hat\lambda = \frac{\hat\sigma_u^2}{(\hat\sigma_u^2 + \hat\sigma_\varepsilon^2)} = \frac{110.40^2}{110.40^2 + 19.91^2 } = 0.97 \]
这是对 Mini Wright meter 测量方法可靠性的一个评价指标。其中\(\sigma_u^2\) 是患者最大呼吸速率(PEFR) 测量值的方差,\(\sigma_\varepsilon^2\) 是测量的随机误差,所以这里的测量方法的可靠度是97%,是可信度十分高的测量准确度。
47.4 随机截距模型中的统计推断
47.4.1 固定效应部分的推断
当数据是平衡数据时,固定效应的 \(\mu\) 的 \(\text{MLE}\) 是总体的均值 (overall mean)。它的估计标准误是:
\[ \hat{\text{SE}}(\hat\mu) = \sqrt{\frac{n\hat\sigma_u^2 + \hat\sigma_\varepsilon^2}{Jn}} \]
记得线性回归中(固定效应模型中),\(\mu\) 的 \(\text{MLE}\) 也还是总体的均值 (overall mean)。它的估计标准误却是:
\[ \hat{\text{SE}}(\hat\mu^F) = \sqrt{\frac{\hat\sigma_\varepsilon^2}{Jn}} \]
所以,仅有固定效应模型时的总体均值的标准误总是要比混合效应模型下估计的总体均值标准误要小
\[ \hat{\text{SE}}(\hat\mu^F) < \hat{\text{SE}}(\hat\mu) \]
如果数据不是平衡数据,那么随机截距模型中 \(\mu\) 的 \(\text{MLE}\) 是每层均值的加权均值 (a weighted mean of the cluster specific means):
\[ \begin{aligned} \hat\mu & = \frac{\sum_jw_j\bar{Y}_{\cdot j}}{\sum_j w_j} \\ \text{Where } w_j & = \frac{1}{\sigma_u^2 + \sigma_\varepsilon^2/n_j} \end{aligned} \]
从加权的方式来看,如果样本量少的层级数据本身的误差方差\(\sigma_\varepsilon^2\) 也较小,那么层样本量较小的层也会和层样本量较大的层获得相似的均值权重。
零假设是 \(\mu = 0\) 的检验,就计算 \(z\) 检验统计量就可以 (或者 \(z^2\) 的 Wald 检验):
\[ z = \frac{\hat\mu}{\hat{\text{SE}}(\hat\mu)} \] 总体均值的 95% 信赖区间的计算式就是:
\[ \hat\mu \pm z_{0.975}\hat{\text{SE}}(\hat\mu) \]
47.4.2 随机效应部分的推断
总体均值的假设检验搞定了之后,我们肯定还想对随机截距模型拟合的随机效应方差作出是否有意义的假设检验。也就是我们希望能检验零假设 \(\sigma_u^2 = 0\),和替代假设 \(\sigma_u^2 > 0\)。一般情况下大家肯定会想到对含有随机效应的模型和只有固定效应的模型使用 LRT (似然比检验),然后把检验统计量拿去和自由度为 1 的卡方分布做比较。但是其实方差本身永远都是大于等于零的,所以传统的 LRT 在这个零假设时并不适用。
在零假设条件下 \(\sigma_u^2 = 0\),也就是说层内相关在一半的数据中是正相关,另一半数据中是正好相反的负相关,以此相互抵消,方差为零。所以其实这里的LRT 检验统计量应该服从的不是自由度为1 的卡方分布那么简单,而是一种混合卡方分布(自由度1 和自由度为0 的混合卡方分布\(\chi_{0, 1}^2\))。所以应该把模型比较之后计算获得的 \(p\) 值除以2,以获得准确的对 \(\sigma_u^2 = 0\) 检验的 \(p\) 值。
M0 <- nlme::lme(fixed = wm ~ 1, random = ~ 1 | id, data = pefr_long, method = "REML")
M0_fixed<- lm(wm ~ 1, data = pefr_long)
anova(M0, M0_fixed)## Model df AIC BIC logLik Test L.Ratio p-value
## M0 1 3 366.7584 371.2480 -180.3792
## M0_fixed 2 2 411.7192 414.7122 -203.8596 1 vs 2 46.96073 <.0001回到本例中的混合效应模型和固定效应模型的比较来看,LRT本身的 P 值已经 \(<0.0001\),所以除不除以二对推断结果都没有太大影响。也就是本例中的随即截距模型是比固定效应的简单线性回归模型更加适合该数据的模型。
其他注意点:
- 在坑爹的 STATA 里面混合效应模型居然还会输出随机效应方差的 “标准误”,该数字请无视之。
- 当样本拥有足够多的样本量 (其实是第二阶层的层数),极大似然法 (ML) 和限制性极大似然法 (REML) 给出的结果会相当接近。
- 当你比较两个不是互为嵌套 (nested) 的模型时,可以使用 AIC/BIC 指标。
47.5 Hierarchical例2
47.5.1 数据
- GHQ 数据
该数据包含 12 名学生前后两次回答 General Health Questionnaire (GHQ) 问卷获得的数据。该问卷用于测量学生的心理压力,其变量名和含义如下:
id Student identifier
GHQ1 General Health Questionnaire score- 1st occasion
GHQ2 General Health Questionnaire score- 2nd occasion- Siblings 数据
该数据是来自一项对 3978 名妈妈关于她们 8604 名孩子的出生体重及健康状况的问卷调查。该数据的变量名和含义如下:
momid Mother identifier
idx Baby identifier
mage Maternal age (years)
meduc Maternal education
gestat gestational age (weeks)
birwt Birth weight (g)
smoke Maternal smoking (0 = no, 1 = yes)
male Baby boy (0 = no, 1 = yes)
year Year of birth
married Maternal marital status (0 = no, 1 = yes)
hsgrad Maternal high school education (0 = no, 1 = yes)
black Maternal race (1 = black, 0 = other)47.5.2 读入 GHQ 数据,探索其内容,该数据是否是平衡数据 (balanced)?计算每名学生的两次问卷成绩平均分。
## # A tibble: 12 × 3
## id GHQ1 GHQ2
## <dbl> <dbl> <dbl>
## 1 1 12 12
## 2 2 8 7
## 3 3 22 24
## 4 4 10 14
## 5 5 10 8
## 6 6 6 4
## 7 7 8 5
## 8 8 4 6
## 9 9 14 14
## 10 10 6 5
## 11 11 2 5
## 12 12 22 16ghq <- ghq %>%
mutate(mean = (GHQ1 + GHQ2)/2)
# each student has 2 observations (i.e. n_j = n = 2)
# and therefore the data are balanced.
# the overall mean is 10.167 and its SD is 6.073
ghq %>%
summarise(OverallMean = mean(mean), SD = sd(mean))## # A tibble: 1 × 2
## OverallMean SD
## <dbl> <dbl>
## 1 10.2 6.0747.5.3 把数据从宽 (wide) 改变成长 (long) 的形式
# transform data into long format
ghq_long <- ghq %>%
gather(key, value, -id, -mean) %>%
separate(key, into = c("measurement", "occasion"), sep = 3) %>%
arrange(id, occasion) %>%
spread(measurement, value)
ghq_long## # A tibble: 24 × 4
## id mean occasion GHQ
## <dbl> <dbl> <chr> <dbl>
## 1 1 12 1 12
## 2 1 12 2 12
## 3 2 7.5 1 8
## 4 2 7.5 2 7
## 5 3 23 1 22
## 6 3 23 2 24
## 7 4 12 1 10
## 8 4 12 2 14
## 9 5 9 1 10
## 10 5 9 2 8
## # ℹ 14 more rows# after reshaping there are 24 records. the summary statistics are
# overall mean sd and min max
ghq_long %>%
summarise(OverallMean = mean(GHQ), SD = sd(GHQ), Min = min(GHQ), Max = max(GHQ))## # A tibble: 1 × 4
## OverallMean SD Min Max
## <dbl> <dbl> <dbl> <dbl>
## 1 10.2 6.10 2 24# between groups mean sd and min
ghq_long %>%
distinct(id, .keep_all= TRUE) %>%
summarise(Bet_mean = mean(mean), Bet_sd = sd(mean), Bet_min = min(mean), Bet_max = max(mean))## # A tibble: 1 × 4
## Bet_mean Bet_sd Bet_min Bet_max
## <dbl> <dbl> <dbl> <dbl>
## 1 10.2 6.07 3.5 23# within groups mean sd and min (came from the difference between
# the overall mean and the within difference) observations for
# each group = 2
ghq_long <- ghq_long %>%
mutate(dif_GHQ = mean(GHQ) - (GHQ - mean))
ghq_long %>%
summarise(N = n(),
Wit_mean = mean(dif_GHQ), Wit_sd = sd(dif_GHQ),
Wit_min = min(dif_GHQ), Wit_max = max(dif_GHQ))## # A tibble: 1 × 5
## N Wit_mean Wit_sd Wit_min Wit_max
## <int> <dbl> <dbl> <dbl> <dbl>
## 1 24 10.2 1.38 7.17 13.2GHQ 的分布并不左右对称。
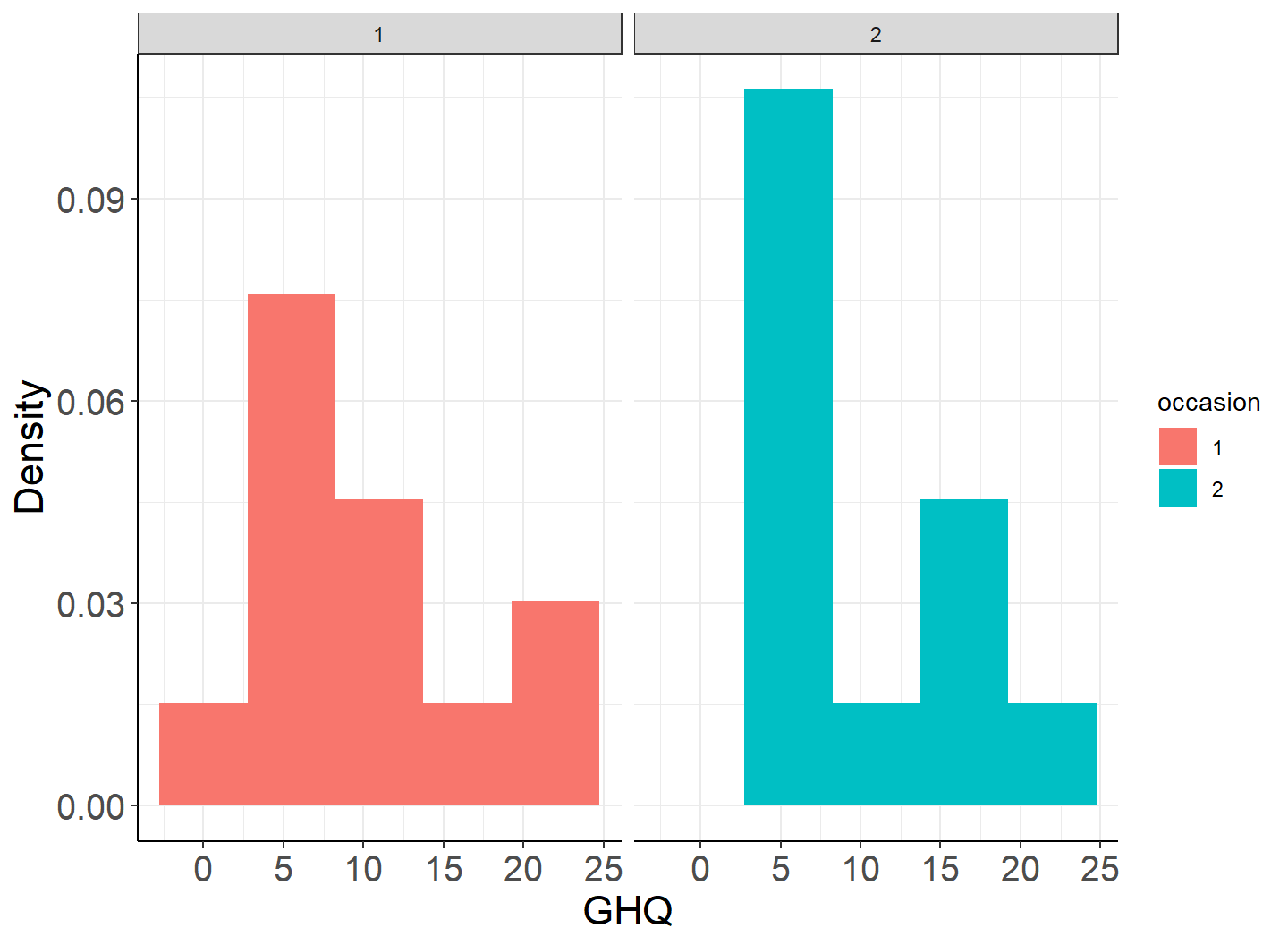
图 47.1: Histogram of GHQ by occasion
47.5.4 对数据按照 id 分层进行 ANOVA
## Analysis of Variance Table
##
## Response: GHQ
## Df Sum Sq Mean Sq F value Pr(>F)
## factor(id) 11 811.33 73.758 20.116 4.778e-06 ***
## Residuals 12 44.00 3.667
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Linear mixed model fit by REML ['lmerMod']
## Formula: GHQ ~ (1 | id)
## Data: ghq_long
## REML criterion at convergence: 131.3492
## Random effects:
## Groups Name Std.Dev.
## id (Intercept) 5.920
## Residual 1.915
## Number of obs: 24, groups: id, 12
## Fixed Effects:
## (Intercept)
## 10.17\(\sigma_u, \sigma_e\) 的估计值分别是 5.92 (between), 1.91 (within)。可以计算层间相关系数 (intra-class correlation) \(\hat\lambda = \frac{\sigma^2_u}{\sigma^2_u + \sigma^2_e} = 0.905\)。且\(\hat\sigma_u = \sqrt{\frac{73.8 - 3.7}{2}} = 5.92\),和前一次练习一样地,这个随机效应的方差,可以通过方差分析表格来直接手动计算(当且仅当分层数据是平衡状态的)。和前面计算的样本数据比较,样本层间标准差是高估了的(sample between variance = 6.073 > 5.92),相反样本层内标准差(within sd) 则是低估了的(sample within sd = 1.383 < 1.91 )。两个层内标准差的关系是:
\[ \sqrt{1.383^2\times\frac{23}{12}} = 1.91 \]
47.5.5 用 R 里的 nlme 包,使用限制性极大似然法 (restricted maximum likelihood, REML) 拟合截距混合效应模型,比较其结果和前文中随机效应 ANOVA 的结果
## Linear mixed-effects model fit by REML
## Data: ghq_long
## AIC BIC logLik
## 137.3492 140.7557 -65.67462
##
## Random effects:
## Formula: ~1 | id
## (Intercept) Residual
## StdDev: 5.919918 1.914855
##
## Fixed effects: GHQ ~ 1
## Value Std.Error DF t-value p-value
## (Intercept) 10.16667 1.753063 12 5.799373 1e-04
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -1.33737204 -0.57848270 0.07355753 0.41405998 1.79602488
##
## Number of Observations: 24
## Number of Groups: 12截距混合效应模型的参数估计和随机效应 ANOVA 的参数估计是一样的。
47.5.6 用极大似然法 (maximum likelihood, ML) method = "ML" 重新拟合前面的混合效应模型,比较结果有什么不同。
#( fit <- lmer(GHQ ~ (1|id), data=ghq_long, REML = FALSE) ) # same but from `lme4` package
summary(nlme::lme(fixed = GHQ ~ 1, random = ~ 1 | id, data = ghq_long, method = "ML"))## Linear mixed-effects model fit by maximum likelihood
## Data: ghq_long
## AIC BIC logLik
## 140.2657 143.7999 -67.13286
##
## Random effects:
## Formula: ~1 | id
## (Intercept) Residual
## StdDev: 5.654398 1.914854
##
## Fixed effects: GHQ ~ 1
## Value Std.Error DF t-value p-value
## (Intercept) 10.16667 1.71453 12 5.929711 1e-04
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -1.31652454 -0.58359637 0.08024454 0.40422622 1.81687284
##
## Number of Observations: 24
## Number of Groups: 12用极大似然法估计的随机残差标准差 \(\sigma_e\) 和 REML/ANOVA 法估计的相同,但是随机效应标准差 \(\sigma_u\) 略小 5.65 < 5.92。
47.5.7 用简单线性回归拟合一个固定效应模型
##
## Call:
## lm(formula = GHQ - mean(GHQ) ~ 0 + factor(id), data = ghq_long)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3 -1 0 1 3
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## factor(id)1 1.833 1.354 1.354 0.200685
## factor(id)2 -2.667 1.354 -1.969 0.072426 .
## factor(id)3 12.833 1.354 9.478 6.37e-07 ***
## factor(id)4 1.833 1.354 1.354 0.200685
## factor(id)5 -1.167 1.354 -0.862 0.405774
## factor(id)6 -5.167 1.354 -3.816 0.002458 **
## factor(id)7 -3.667 1.354 -2.708 0.019025 *
## factor(id)8 -5.167 1.354 -3.816 0.002458 **
## factor(id)9 3.833 1.354 2.831 0.015145 *
## factor(id)10 -4.667 1.354 -3.447 0.004836 **
## factor(id)11 -6.667 1.354 -4.924 0.000352 ***
## factor(id)12 8.833 1.354 6.524 2.84e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.915 on 12 degrees of freedom
## Multiple R-squared: 0.9486, Adjusted R-squared: 0.8971
## F-statistic: 18.44 on 12 and 12 DF, p-value: 6.836e-06可以看到输出报告最底段部分 Residual standard error: 1.91 on 12 degrees of freedom 就是前文三种不同模型拟合的随机残差效应的标准差。在 STATA 里被叫做 Root MSE。
47.5.8 计算这些随机截距的均值和标准差
## [1] 7.585801e-16## [1] 6.072791这里仅仅用固定效应模型时,不同群截距的均值虽然和用混合效应模型估计的一样为零,但是其估计的标准差要大于无论是REML (5.92) 或者是ML (5.65) 估计值的大小,其实这里简单线性回归给出的截距均值,就是本练习一开始让你计算的样本均值的标准差(between group sd)。这是因为简单线性回归 (固定效应模型) 忽视了这些不同组的均值的不确定性。
47.5.9 忽略掉所有的分层和解释变量拟合 GHQ 的简单线性回归
##
## Call:
## lm(formula = GHQ ~ 1, data = ghq_long)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.167 -4.417 -2.167 3.833 13.833
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.167 1.245 8.167 3e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.098 on 23 degrees of freedom此时的模型估计的 Residual standard error: 6.09 on 23 degrees of freedom 其实就是一开始让你计算的样本整体的标准差 (overall sd)
47.5.10 用分层的稳健法 (三明治标准误法) 计算简单线性回归时,截距的标准误差,和简单线性回归时的结果作比较
# sandwich robust method with cluster id
robustReg <- clubSandwich::coef_test(Fixed_simple, vcov = "CR1", cluster = ghq_long$id)
rob.std.err <- robustReg$SE
naive.std.err<-summary(Fixed_simple)$coefficients[,2]
better.table <- cbind("Estimate" = coef(Fixed_simple),
"Naive SE" = naive.std.err,
"Pr(>|z|)" = 2 * pt(abs(coef(Fixed_simple)/naive.std.err), df=nrow(ghq_long)-2, lower.tail = FALSE),
"LL" = coef(Fixed_simple) - 1.96 * naive.std.err,
"UL" = coef(Fixed_simple) + 1.96 * naive.std.err,
"Robust SE" = rob.std.err,
"Pr(>|z|)" = 2 * pt(abs(coef(Fixed_simple)/rob.std.err), df=nrow(ghq_long)-2,
lower.tail = FALSE),
"LL" = coef(Fixed_simple) - qt(df=robustReg$df, 0.975) * rob.std.err,
"UL" = coef(Fixed_simple) + qt(df=robustReg$df, 0.975) * rob.std.err)
rownames(better.table)<-c("Constant")
better.table## Estimate Naive SE Pr(>|z|) LL UL Robust SE Pr(>|z|)
## Constant 10.16667 1.244796 4.179246e-08 7.726867 12.60647 1.753064 7.79687e-06
## LL UL
## Constant 6.308199 14.0251347.5.11 读入 siblings 数据。先总结婴儿的出生体重,思考这个数据中婴儿出生体重之间是否可能存在关联性?它的来源是哪里。用这个数据拟合两个混合效应模型 (ML, REML),不加入任何解释变量。
siblings <- read_dta("../Datas/siblings.dta")
Fixed_ml <- nlme::lme(fixed = birwt ~ 1, random = ~ 1 | momid, data = siblings, method = "ML")
summary(Fixed_ml)## Linear mixed-effects model fit by maximum likelihood
## Data: siblings
## AIC BIC logLik
## 130957 130978.2 -65475.49
##
## Random effects:
## Formula: ~1 | momid
## (Intercept) Residual
## StdDev: 368.2866 377.6578
##
## Fixed effects: birwt ~ 1
## Value Std.Error DF t-value p-value
## (Intercept) 3467.969 7.138068 4626 485.8414 0
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -6.274585259 -0.486039856 0.003605009 0.505434867 4.050612925
##
## Number of Observations: 8604
## Number of Groups: 3978Fixed_reml <- nlme::lme(fixed = birwt ~ 1, random = ~ 1 | momid, data = siblings, method = "REML")
summary(Fixed_reml)## Linear mixed-effects model fit by REML
## Data: siblings
## AIC BIC logLik
## 130951.2 130972.4 -65472.6
##
## Random effects:
## Formula: ~1 | momid
## (Intercept) Residual
## StdDev: 368.356 377.6577
##
## Fixed effects: birwt ~ 1
## Value Std.Error DF t-value p-value
## (Intercept) 3467.969 7.138555 4626 485.8082 0
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -6.274306389 -0.486019398 0.003529979 0.505355037 4.050392366
##
## Number of Observations: 8604
## Number of Groups: 3978由于该数据样本量足够大 (混合效应模型中等同于说数据的层数足够多),你可以看到其实 ML 法和 REML 法估计的参数结果十分地接近。