第 27 章 多元模型分析:矩阵标记与其意义
在线性回归目前为止介绍的内容中,我们最多只谈到了预测变量为两个的情况。本章,我们要把这些概念推广到三个或者三个以上预测变量的情况。同时,多重线性回归时采用的假设检验也会被谈及。其实最常见的就是 \(F\) 检验。而且我们也见识过了,当预测变量只有一个的时候,\(F\) 检验和 \(t\) 检验是等价的。
重要的概念我们都已经介绍完毕。前一章的多重回归模型中也强调了,我们之所以希望把多个预测变量放进模型,最大的目的就是想了解这些预测变量之间的相互关系,当他们得到调整(adjustment) 之后,彼此之间的关系是怎样的。这样的关系我们称之为条件关系 (conditional relationships)。当我们使用条件关系的称呼时,需要同时指明我们说的是哪个变量,在那个变量不变的条件下,与因变量的关系是如何如何。
本章节最后的部分将会着重关注共线性 (collinearity) 的问题。
27.1 线性回归模型的矩阵/非矩阵标记法
27.1.1 模型标记:
假如,因变量用 \(Y\) 表示,预测变量有 \(p\) 个之多 \((X_1,\cdots, X_p)\)。该模型的非矩阵标记法如下: \[ \begin{equation} y_i = \alpha + \beta_1 x_{1i}+ \beta_2 x_{2i} + \cdots + \beta_p x_{pi} + \varepsilon_i \text{ with } \varepsilon_i \sim \text{NID}(0, \sigma ^2) \end{equation} \tag{27.1} \] 其中,
- \(y_i =\) 第 \(i\) 名观察对象的因变量数据;
- \(x_{pi} =\) 第 \(i\) 名观察对象的第 \(p\) 个预测变量的观察数据。
上面的非矩阵标记法,等同于如下的矩阵标记法: \[ \begin{equation} \textbf{Y} = \textbf{X}\beta+\varepsilon, \text{ where } \varepsilon \sim N(0, \textbf{I}\sigma^2) \\ \left( \begin{array}{c} y_1\\ y_2\\ \vdots\\ y_n \end{array} \right) = \left( \begin{array}{c} 1& x_{11} & \cdots & x_{p1} \\ 1& x_{12} & \cdots & x_{p2} \\ \vdots & \vdots& \vdots & \vdots \\ 1& x_{1n}& \cdots &x_{pn} \\ \end{array} \right)\left( \begin{array}{c} \alpha \\ \beta_1\\ \beta_2 \\ \vdots \\ \beta_p \end{array} \right)+\left( \begin{array}{c} \varepsilon_1\\ \varepsilon_2\\ \vdots\\ \varepsilon_n\\ \end{array} \right) \end{equation} \tag{27.2} \] 此公式 (27.2) 中
- \(\textbf{X}\) 是一个 \(n\times(p+1)\) 的矩阵;
- \(\textbf{Y}\) 和 \(\varepsilon\) 分别是长度为 \(n\) 的列向量;
- \(\beta\) 是长度为 \(p+1\) 的列向量,且第一个元素是 \(\alpha\),偶尔被人误写成 \(\beta_0\)。
残差被认为服从多元正态分布 (multivariate normal distribution),这个多元正态分布的方差协方差矩阵等于 \(\sigma^2\) 与单位矩阵相乘获得的矩阵。这其实等价于认为残差服从独立正态且方差为 \(\sigma^2\) 的分布,
27.2 解读参数
模型中的参数的涵义为:
- \(\alpha\) 是截距,所有的预测变量都是零的时候,因变量 \(Y\) 的期待值大小;
- \(\beta_j\) 是预测变量 \(X_j\) 升高一个单位,且其他变量保持不变的同时,因变量 \(Y\) 的期待值的变化;
- \(\beta_j\) 都是偏回归系数,每个偏回归系数,测量的都是该预测变量调整了其他预测变量之后对于因变量期待值的影响。
27.2.1 最小二乘估计
还是同之前一样,我们对残差的平方和最小化,来获取我们关心的预测变量的回归变量。
\[ \begin{aligned} SS_{RES} & = \sum_{i=1}^n \hat\varepsilon_i^2 = \sum_{i=1}^n(y_i-\hat{y})^2 \\ & = \sum_{i=1}^n (y_i-\hat\alpha-\hat\beta_1x_{1i}-\hat\beta_2x_{2i}-\cdots-\hat\beta_px_{pi})^2 \end{aligned} \tag{27.3} \]
下面用矩阵标记法计算 \(\hat\beta\):
\[ \begin{aligned} \text{Because } \mathbf{Y} & = \mathbf{X\hat\beta + \varepsilon} \\ \Rightarrow \mathbf{\varepsilon} & = \mathbf{Y - X\hat\beta}\\ \Rightarrow \mathbf{SS_{RES}} & = \varepsilon_1\times \varepsilon_1 + \varepsilon_2\times \varepsilon_2 + \cdots + \varepsilon_n\times \varepsilon_n \\ & = (\varepsilon_1, \varepsilon_2, \cdots, \varepsilon_n)\left( \begin{array}{c} \varepsilon_1\\ \varepsilon_2\\ \vdots\\ \varepsilon_n \end{array} \right) \\ & = \mathbf{\varepsilon^\prime} \mathbf{\varepsilon} \\ & = \mathbf{(Y-X\hat\beta)^\prime(Y-X\hat\beta)} \\ & = \mathbf{Y^\prime Y - X^\prime\hat\beta^\prime Y - Y^\prime X\hat\beta + X^\prime\hat\beta^\prime X \hat\beta } \\ \text{Because} &\text{ transpose of a scalar is a scalar:} \\ \mathbf{Y^\prime X\hat\beta} & = \mathbf{(Y^\prime X\hat\beta)^\prime = X^\prime\hat\beta^\prime Y} \\ \Rightarrow \mathbf{SS_{RES}} & = \mathbf{Y^\prime Y - 2X^\prime\hat\beta^\prime Y + X^\prime\hat\beta^\prime X \hat\beta }\\ \Rightarrow \mathbf{\frac{\partial SS_{RES}}{\partial \hat\beta}} & = \mathbf{-2X^\prime Y + 2 X^\prime X \hat\beta} = 0 \ \ \Rightarrow \mathbf{\hat\beta} & = \mathbf{(X^\prime X)^{-1}X^\prime Y} \end{aligned} \tag{27.4} \]
公式(27.4) 是参数矩阵\(\mathbf{\beta}\) 的无偏估计,且服从方差协方差矩阵为\(\mathbf{(X^\prime X)^{-1} \sigma^2}\) 的多元正态分布:
\[ \begin{equation} \mathbf{\hat\beta} \sim N(\mathbf{\beta, (X^\prime X)^{-1}\sigma^2}) \end{equation} \tag{27.5} \]
另外可以被证明的是,多元线性回归模型的残差方差的估计量计算公式为:
\[ \begin{aligned} \hat\sigma^2 & = \sum^n_{i=1}\frac{\hat\varepsilon^2_i}{[n-(p+1)]} \\ & = \sum^n_{i=1}\frac{\sum_{i=1}^n (y_i-\hat\alpha-\hat\beta_1x_{1i}-\hat\beta_2x_{2i}-\cdots- \hat\beta_px_{pi})^2}{[n-(p+1)]} \\ \text{Where } & p \text{ is the number of predictors} \end{aligned} \tag{27.6} \]
27.2.2 因变量的期待值 \(\mathbf{\hat Y}\)
因变量的期待值矩阵 \(\mathbf{\hat Y}\) 根据公式 (27.4) 推导:
\[ \begin{aligned} \mathbf{\hat Y} & = \mathbf{X\hat\beta} \\ & = \mathbf{X(X^\prime X)^{-1}X^\prime Y}= \mathbf{PY} \\ \text{Where } \mathbf{P} &= \mathbf{X(X^\prime X)^{-1}X^\prime} \end{aligned} \tag{27.7} \]
这里的 \(n\times n\) 的正方形矩阵 \(\mathbf{P}\) 在多元线性回归中是一个极为重要的矩阵。
- 它常被叫做“帽子/映射 (hat/projection)”矩阵,因为它把观察值 \(\mathbf{Y}\) 和观察值的拟合值一一映射;
- 帽子矩阵的第 \(i\) 个对角元素,是第 \(i\) 名观察值的影响值 (leverage),会用在下章节的模型诊断中;
- 拟合值矩阵的方差协方差矩阵被定义为:
\[ \begin{equation} \text{Var}(\mathbf{\hat Y}) = \mathbf{P}\sigma^2 \end{equation} \tag{27.8} \]
27.2.3 残差
残差的观察值 \(\mathbf{\hat\varepsilon}\) 被定义为观察值和拟合值的差。根据前节 (27.8) 推导:
\[ \begin{equation} \mathbf{\hat\varepsilon} = \mathbf{Y - \hat Y} = \mathbf{Y - PY} = \mathbf{(I - P)Y} \end{equation} \tag{27.9} \]
这个观察残差的方差被定义为:
\[ \begin{equation} \text{Var}(\mathbf{\hat\varepsilon}) = \mathbf{(I - P)}\sigma^2 \end{equation} \tag{27.10} \]
- 一般地,\(\mathbf{P}\) 不是一个对角矩阵,意思是观察残差之间无法保证是独立的;
- \(\mathbf{P}\) 的对角元素也不全都相等,意思是观察残差的方差无法保证是恒定不变的。
27.3 方差分析一般化和 \(F\) 检验
27.3.1 多元线性回归时的决定系数和残差方差
和简单线性回归一样,因变量的校正平方和可以被分割成两部分:回归模型能够解释的平方和;模型无法解释的残差平方和。类比方差分析章节 (Section 25) 的公式 (25.1):
\[ \begin{aligned} \sum_{i=1}^n(y_i-\bar{y})^2 & = \sum_{i=1}^n(\hat{y}_i - \bar{y})^2 + \sum_ {i=1}^n(y_i - \hat{y}_i)^2 \\ SS_{yy} & = SS_{REG} + SS_{RES} \end{aligned} \tag{27.11} \]
和简单线性回归也一样,多元线性回归时的模型决定系数 (coefficient of determination) 的定义为:
\[ \begin{aligned} R^2 & = \frac{SS_{yy}-SS_{RES}}{SS_{yy}} = 1- \frac{SS_{RES}}{SS_{yy}} \\ & = 1 - \frac{\sum_{i=1}^n(y_i-\hat{y}_i)^2}{\sum_{i=1}^n(y_i - \bar{y})^2 } \end{aligned} \tag{27.12} \]
这里的 \(R^2\) 也一样可以被解释为模型能够解释的因变量变动部分的百分比 (proportion of the variability in the dependent variable explained by the model)。值得注意的是,当模型中预测变量不减少,每加入一个新的预测变量,决定系数也会增加,相反残差平方和却绝不会增加。
27.3.2 方差分析表格
下表和简单线性回归的方差分析表格很类似,也可以用来作假设检验(回归方程的显著性检验Global \(F-\text{test}\),和偏\(F\) 检验Partial \(F-\text {test}\))。
|
Source of Variation |
Sum of Squares |
Degrees of Freedom |
Mean Sum of Squares |
|---|---|---|---|
| Regression (model) | \(SS_{REG}\) | \(p\) | \(MS_{REG} = \frac{SS_{REG}}{p}\) |
| Residual | \(SS_{RES}\) | \(n-(p+1)\) | \(MS_{RES} = \frac{SS_{RES}}{[n-(p+1)]}\) |
| Total | \(SS_{yy}\) | \(n-1\) | \(\frac{SS_{yy}}{(n-1)}\) |
27.3.3 回归方程的显著性检验
整个方程的显著性检验,检验的是所有的回归系数都等于零的零假设,其对应的替代假设则是:“回归系数不全为零”。就是至少有一个不等于零。
在零假设条件下,检验统计量的计算公式为:
\[ \begin{equation} F = \frac{MS_{REG}}{MS_{RES}} \sim F_{p, [n-(p+1)]} \end{equation} \tag{27.13} \]
在零假设条件下,\(F\) 的期望值接近\(1\),而替代假设条件下的\(F\) 总是会大于此,所以和\(F\) 分布比较特征值时只需要比较单侧的(右侧的)值,即可获得双侧\(p\) 值。
在 R 里面,回归方程的结果的最底下会出现统计量 \(F\) 的大小,但是 \(MS_{REG}, MS_{RES}\) 要用 anova() 代码获得:
growgam1 <- read_dta("../Datas/growgam1.dta")
growgam1$sex <- as.factor(growgam1$sex)
Model1 <- lm(wt ~ age + len, data=growgam1)
print(summary(Model1), digits = 5)##
## Call:
## lm(formula = wt ~ age + len, data = growgam1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.20525 -0.64402 -0.00303 0.55967 2.86277
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -8.351244 1.259968 -6.6281 3.531e-10 ***
## age -0.011260 0.016751 -0.6722 0.5023
## len 0.237129 0.019516 12.1502 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.95456 on 187 degrees of freedom
## Multiple R-squared: 0.74337, Adjusted R-squared: 0.74063
## F-statistic: 270.84 on 2 and 187 DF, p-value: < 2.22e-16## Analysis of Variance Table
##
## Response: wt
## Df Sum Sq Mean Sq F value Pr(>F)
## age 1 359.06 359.06 394.06 < 2.2e-16 ***
## len 1 134.52 134.52 147.63 < 2.2e-16 ***
## Residuals 187 170.39 0.91
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1可以看到summary() 输出结果的最后一行是关于回归方程整体的\(F\) 检验结果F-statistic: 270.84 on 2 and 187 DF, p-value: < 2.22e-16,从anova () 结果中可以获得\(MS_{REG} = \frac{359.0632 + 134.5153}{2} = 246.7892\)。 \(F_{2,187} = \frac{246.7892}{0.9111833} = 270.84\)。这个检验结果证明了,两个预测变量 “体重” 和 “身长” 至少有一个的回归系数不等于零。
27.3.4 \(\text{partial }F\) 检验
如果我们建立两个模型,一个稍微复杂一些 \((B)\),比起略简单的模型 \((A)\),增加了 \(k\) 个预测变量。两个模型放在一起的方差分析表格可以归纳成:
|
Source of Variation |
Sum of Squares |
Degrees of Freedom |
Mean Sum of Squares |
|---|---|---|---|
|
Explained by model \(A\) |
\(SS_{REG_A}\) | \(p-k\) | \(MS_{REG_A} = \frac{SS_{REG_A}}{p-k}\) |
|
Extra Explained by model \(B\) |
\(SS_{REG_B}-SS_{REG_A}\) | \(k\) | \(\frac{SS_{REG_B}-SS_{REG_A}}{k}\) |
|
Residual from model \(B\) |
\(SS_{RES_B}\) | \(n-(p+1)\) | \(MS_{RES_B} = \frac{SS_{RES_B}}{[n-(p+1)]}\) |
| Total | \(SS_{yy}\) | \(n-1\) | \(\frac{SS_{yy}}{(n-1)}\) |
那么偏 \(F\) 检验的零假设就是:\(B\) 模型中包含,\(A\) 模型中不包含的 \(k\) 个预测变量的回归系数都等于零。
\[ \begin{equation} F=\frac{(SS_{REG-B}-SS_{REG-A})/k}{MS_{RES-B}} \sim F_{k, [n-(p+1)]} \end{equation} \tag{27.14} \]
在 R 里建立两个模型:
##
## Call:
## lm(formula = wt ~ len, data = growgam1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.155217 -0.629239 0.014555 0.544783 2.928738
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.6694406 0.7463556 -10.276 < 2.2e-16 ***
## len 0.2257467 0.0096893 23.299 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.95317 on 188 degrees of freedom
## Multiple R-squared: 0.74275, Adjusted R-squared: 0.74139
## F-statistic: 542.82 on 1 and 188 DF, p-value: < 2.22e-16## Analysis of Variance Table
##
## Response: wt
## Df Sum Sq Mean Sq F value Pr(>F)
## len 1 493.17 493.17 542.82 < 2.2e-16 ***
## Residuals 188 170.80 0.91
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = wt ~ len + age + sex, data = growgam1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.110422 -0.648401 0.026103 0.560621 2.768583
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.8906758 1.3003091 -6.0683 7.091e-09 ***
## len 0.2317997 0.0198470 11.6793 < 2.2e-16 ***
## age -0.0077959 0.0168974 -0.4614 0.6451
## sex2 -0.1964758 0.1421171 -1.3825 0.1685
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.95224 on 186 degrees of freedom
## Multiple R-squared: 0.74599, Adjusted R-squared: 0.74189
## F-statistic: 182.08 on 3 and 186 DF, p-value: < 2.22e-16## Analysis of Variance Table
##
## Response: wt
## Df Sum Sq Mean Sq F value Pr(>F)
## len 1 493.17 493.17 543.8753 <2e-16 ***
## age 1 0.41 0.41 0.4540 0.5013
## sex 1 1.73 1.73 1.9113 0.1685
## Residuals 186 168.66 0.91
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1根据公式 (27.14),\(F=\frac{0.4116944+1.7330862}{2\times0.9067645} = 1.18\)。 \(p\) 值可以在 R 里面这样计算:
## [1] 0.3087575更方便的是直接用 anova() 进行偏 \(F\) 检验:
## Analysis of Variance Table
##
## Model 1: wt ~ len
## Model 2: wt ~ len + age + sex
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 188 170.80
## 2 186 168.66 2 2.1448 1.1827 0.308827.4 添加新变量对回归模型的影响
当你决定给建立的模型 \(\mathbf{A}\) 增加新的预测变量时,输出的结果改变的有:
- 模型 \(\mathbf{A}\) 原先的预测变量的偏回归系数会改变;
- 模型 \(\mathbf{A}\) 原先的预测变量的偏回归系数的方差会改变;
- 模型 \(\mathbf{A}\) 原先的预测变量的偏回归系数的检验结果会改变;
- 模型 \(\mathbf{A}\) 原先的 拟合值 (predicted values/fitted values)会改变;
- 决定系数 \(R^2\) 会改变。
27.4.1 偏回归系数方差的改变
偏回归系数矩阵\(\mathbf{\hat\beta}\) 的方差\(\mathbf{(X^\prime X)^{-1}\sigma^2}\) (27.5),取决于
- 残差方差 (residual variance) \(\sigma^2\);
- 样本量大小 (sample size) \(n\);
- 预测变量之间的协方差 (covariance between the predictor variable in question and the others)。
在简单线性回归中,预测变量的变化性 (variability,用方差或标准差衡量) 越大,回归系数的估计就越精确。类似地,多元线性回归中,预测变量之间的协方差之所以重要,因为它决定了其他预测变量保持不变时,该预测变量的变化性。如果某两个预测变量之间高度相关 (high covariance),那么当一个预测变量保持不变时,另一个的变化性就很小。
所以当给一个模型加入新的预测变量时,可能观察的现象是原先模型中已有的预测变量的偏回归系数的方差可能升高,也可能降低。
- 如果新加入的变量能解释很大比例的残差方差,那么其他原有变量的偏回归系数会降低 (变精确);
- 如果新加入的变量和原模型中的某个变量高度相关,那么加入新变量后,原模型中与之高度相关的预测变量的方差会升高(不精确),这个现象会在共线性( collinearity) 中继续讨论。
27.4.5 共线性
当预测变量 \(X_1\) 和另一个预测变量 \(X_2\) 之间呈高度线性关系时被定义为共线性 ( collinearity)现象。如果这两个变量的关系是完全线性(exact linear),那么多元回归其实是无法进行的,因为这两个变量中的一个随着另一个改变,无法像我们设想的那样把其中一个变量保持不变,从而估计另一个变量的回归系数。用矩阵表示多元预测变量时\(\mathbf{X}\) 是奇异矩阵singular matrix,\(\mathbf{( X^\prime X)^{-1}}\) 是不存在的。
完全线性的最佳例子是我们在对分类变量使用哑变量的情况下。每个哑变量之间都是完全线性的关系,因而我们只能用 \(0,1\) 来编码哑变量,当某个哑变量存在时,其余的哑变量取 \(0\) 从模型中消失。否则模型将无法拟合。
如果某两个变量之间高度相关,那么他们的预测变量矩阵接近 奇异矩阵,把这两个变量同时作为预测变量放入模型中会引起共线性现象,表现出来的形式有:
- 偏回归系数的方差变得很大;
- 偏回归系数本身的绝对值变得异常大;
- 某些已知的重要预测变量的偏回归系数变得过小且不再有意义;
- 虽然会有 1-3 描述的异常现象出现,但是拟合值的变化却可能微不足道。
所以拟合多元线性回归模型时,极为重要的一点是要避免共线性。如果有些变量高度相关,必须考虑改变他们放入模型的形式:
- 收缩期血压,舒张期血压两个变量是高度相关的,不能一起放入模型中。如果需要同时考虑两个变量,可以用其中一个,另一个预测变量用二者之差;
- 身高,体重常常是高度相关的,尽量不要一起放入模型中,可以使用他们的结合形式体质指数 (BMI, \(\text{kg/m}^2\));
- 当使用二次方程进行模型拟合的时候,用 \((x_i - \bar{x})^2\) 取代 \(x_i^2\)。
27.5 实例
27.5.1 血清维生素 C 浓度的预测变量
数据来自与某个横断面研究,其目的是找出与血清维生素 C 浓度相关的预测变量。
数据中个变量含义如下表所示。
- 在R 里读入数据,并对数据内容总结,对维生素C浓度和其他连续性变量作散点图,对分类变量如性别,吸烟状况,和维生素C补充剂服用与否之间的维生素C 浓度作初步的分析表格。
library(haven)
library(tidyverse)
vitC <- read_dta("../Datas/vitC.dta")
# Recoding the categorical variables
vitC <- vitC %>%
mutate(sex = as.factor(sex)) %>%
mutate(sex = fct_recode(sex,
Men = "0",
Women = "1")) %>%
mutate(cigs = as.factor(cigs)) %>%
mutate(cigs = fct_recode(cigs,
"Non-smoker" = "0",
"Smoker" = "1")) %>%
mutate(ctakers = as.factor(ctakers)) %>%
mutate(ctakers = fct_recode(ctakers,
No = "0",
Yes = "1"))
summary(vitC) ## serial age height cigs
## Min. : 1.00 Min. :65.00 Min. :1.480 Non-smoker:80
## 1st Qu.: 23.75 1st Qu.:67.00 1st Qu.:1.580 Smoker :12
## Median : 49.00 Median :69.00 Median :1.640
## Mean : 49.25 Mean :69.32 Mean :1.647
## 3rd Qu.: 73.25 3rd Qu.:71.00 3rd Qu.:1.720
## Max. :100.00 Max. :74.00 Max. :1.890
## NA's :1
## weight sex seruvitc ctakers
## Min. : 44.00 Men :44 Min. : 8.00 No :73
## 1st Qu.: 57.80 Women:48 1st Qu.: 34.75 Yes:19
## Median : 67.00 Median : 58.00
## Mean : 68.57 Mean : 53.21
## 3rd Qu.: 76.55 3rd Qu.: 71.00
## Max. :103.00 Max. :100.00
## NA's :1## # A tibble: 6 × 8
## serial age height cigs weight sex seruvitc ctakers
## <dbl> <dbl> <dbl> <fct> <dbl> <fct> <dbl> <fct>
## 1 1 71 1.72 Smoker 68.8 Men 9 No
## 2 2 70 1.63 Non-smoker 58.2 Women 19 No
## 3 3 69 1.65 Non-smoker 94.3 Women 69 Yes
## 4 4 67 1.62 Non-smoker 87.6 Women 71 No
## 5 5 68 1.53 Non-smoker 66.3 Women 87 Yes
## 6 6 71 1.64 Non-smoker 72.2 Women 96 Yes## vars n mean sd median trimmed mad min max range skew
## serial 1 92 49.25 29.07 49.00 48.97 37.06 1.00 100.00 99.00 0.04
## age 2 92 69.32 2.91 69.00 69.27 2.97 65.00 74.00 9.00 0.15
## height 3 91 1.65 0.10 1.64 1.64 0.10 1.48 1.89 0.41 0.33
## cigs* 4 92 1.13 0.34 1.00 1.04 0.00 1.00 2.00 1.00 2.16
## weight 5 91 68.57 13.48 67.00 67.92 14.08 44.00 103.00 59.00 0.41
## sex* 6 92 1.52 0.50 2.00 1.53 0.00 1.00 2.00 1.00 -0.09
## seruvitc 7 92 53.21 23.83 58.00 54.16 22.24 8.00 100.00 92.00 -0.40
## ctakers* 8 92 1.21 0.41 1.00 1.14 0.00 1.00 2.00 1.00 1.43
## kurtosis se
## serial -1.23 3.03
## age -1.20 0.30
## height -0.76 0.01
## cigs* 2.69 0.04
## weight -0.42 1.41
## sex* -2.01 0.05
## seruvitc -0.94 2.48
## ctakers* 0.04 0.04## [1] 24## [1] 24从初步的熟悉数据结构和归纳结果可以看出,身高体重两个数据有出现缺损值 (编号 24 的患者)。
# You can also get similar detailed descriptive statistics by groups from package "psych"
describeBy(vitC$seruvitc, group = vitC$sex)##
## Descriptive statistics by group
## group: Men
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 44 46.09 24.88 52.5 45.61 25.95 8 100 92 -0.06 -1.12 3.75
## ------------------------------------------------------------
## group: Women
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 48 59.73 21.04 66.5 61.15 15.57 15 96 81 -0.65 -0.62 3.04##
## Descriptive statistics by group
## group: Non-smoker
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 80 55.14 23.32 58 56.3 22.24 8 100 92 -0.43 -0.85 2.61
## ------------------------------------------------------------
## group: Smoker
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 12 40.33 24.19 49.5 40.7 25.2 9 68 59 -0.19 -1.93 6.98##
## Descriptive statistics by group
## group: No
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 73 48.64 22.79 55 49.47 25.2 8 84 76 -0.33 -1.24 2.67
## ------------------------------------------------------------
## group: Yes
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 19 70.74 19.61 72 72.41 19.27 13 100 87 -1.07 1.52 4.5所以,血清维生素水平在女性,非吸烟者,和服用补充剂(废话) 的人中较高。
par(mfrow=c(2,2))
plot(vitC$age, vitC$seruvitc, pch = 20, xlab = "age on study entry", ylab = "Serum ascorbate")
plot(vitC$weight, vitC$seruvitc, pch = 20, xlab = "Clothed weight", ylab = "Serum ascorbate")
plot(vitC$height, vitC$seruvitc, pch = 20, xlab = "Height", ylab = "Serum ascorbate")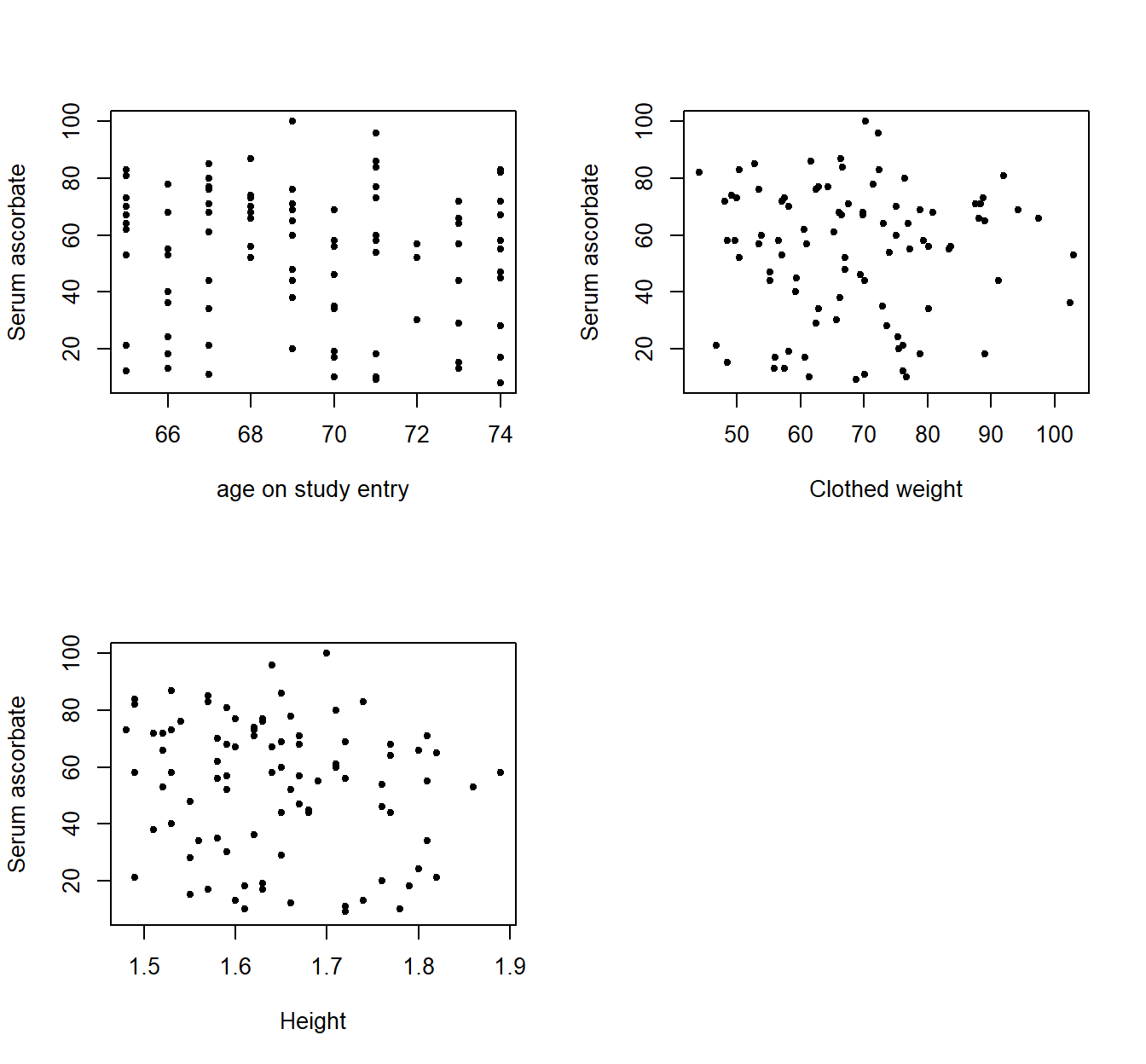
图 27.1: Scatter plots between serum ascorbate and age/weight/height
散点图似乎没有证据提示血清维生素 C 浓度和连续型变量,年龄,身高,体重之间有什么相关性。
- 建立维生素 C 和其他预测变量的简单线性回归模型,你有什么结论?
##
## Call:
## lm(formula = seruvitc ~ age, data = vitC)
##
## Residuals:
## Min 1Q Median 3Q Max
## -44.935 -18.979 5.817 16.669 46.521
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 113.1041 59.5112 1.901 0.0606 .
## age -0.8641 0.8578 -1.007 0.3165
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 23.83 on 90 degrees of freedom
## Multiple R-squared: 0.01115, Adjusted R-squared: 0.0001626
## F-statistic: 1.015 on 1 and 90 DF, p-value: 0.3165## 2.5 % 97.5 %
## (Intercept) -5.125252 231.3335294
## age -2.568324 0.8400563血清维生素 C 浓度随着年龄增加递减,但是回归系数不具有统计学意义 (\(p=0.32\))。年龄每增加 1 岁,血清维生素平均下降 \(0.864 \:\mu\text{mol/L, 95% CI:} (-2.57, 0.840)\),
##
## Call:
## lm(formula = seruvitc ~ height, data = vitC)
##
## Residuals:
## Min 1Q Median 3Q Max
## -45.106 -19.805 5.761 17.936 48.293
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 115.90 41.19 2.814 0.00603 **
## height -37.76 24.96 -1.513 0.13394
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 23.32 on 89 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.02506, Adjusted R-squared: 0.01411
## F-statistic: 2.288 on 1 and 89 DF, p-value: 0.1339## 2.5 % 97.5 %
## (Intercept) 34.05040 197.75111
## height -87.36559 11.84396血清维生素 C 浓度随着身高增加递减,但是回归系数不具有统计学意义 (\(p=0.134\))。身高每增加 1cm,血清维生素平均下降 \(0.378 \:\mu\text{mol/L, 95% CI:} (-0.874, 0.118)\),
##
## Call:
## lm(formula = seruvitc ~ cigs, data = vitC)
##
## Residuals:
## Min 1Q Median 3Q Max
## -47.138 -19.534 3.265 17.863 44.862
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 55.137 2.620 21.049 <2e-16 ***
## cigsSmoker -14.804 7.253 -2.041 0.0442 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 23.43 on 90 degrees of freedom
## Multiple R-squared: 0.04424, Adjusted R-squared: 0.03362
## F-statistic: 4.166 on 1 and 90 DF, p-value: 0.04417## 2.5 % 97.5 %
## (Intercept) 49.93334 60.3416643
## cigsSmoker -29.21385 -0.3944881血清维生素C 浓度与在吸烟人群中较低,与不吸烟人群相比,吸烟人群的血清维生素C 浓度平均低\(14.8 \:\mu\text{mol/L, 95% CI: } (0.394, 29.2)\),这个浓度差具有临界统计学意义\((p=0.044)\)。
##
## Call:
## lm(formula = seruvitc ~ weight, data = vitC)
##
## Residuals:
## Min 1Q Median 3Q Max
## -44.705 -18.388 4.413 17.210 46.281
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 53.04017 12.90016 4.112 8.73e-05 ***
## weight 0.00967 0.18463 0.052 0.958
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 23.61 on 89 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 3.082e-05, Adjusted R-squared: -0.0112
## F-statistic: 0.002743 on 1 and 89 DF, p-value: 0.9583## 2.5 % 97.5 %
## (Intercept) 27.4078254 78.6725063
## weight -0.3571766 0.3765173维生素浓度和体重关系几乎可以忽略 \((p=0.96)\)。
##
## Call:
## lm(formula = seruvitc ~ sex, data = vitC)
##
## Residuals:
## Min 1Q Median 3Q Max
## -44.73 -20.23 6.59 17.27 53.91
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 46.091 3.461 13.319 < 2e-16 ***
## sexWomen 13.638 4.791 2.847 0.00547 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 22.95 on 90 degrees of freedom
## Multiple R-squared: 0.0826, Adjusted R-squared: 0.07241
## F-statistic: 8.104 on 1 and 90 DF, p-value: 0.005472## 2.5 % 97.5 %
## (Intercept) 39.215886 52.96593
## sexWomen 4.120219 23.15630血清维生素C 浓度与在女性中较高,与男性相比,女性的血清维生素C 浓度平均高\(13.6 \:\mu\text{mol/L, 95% CI:} (4.12, 23.2)\),这个浓度差具有显著统计学意义\((p=0.005)\)。
##
## Call:
## lm(formula = seruvitc ~ ctakers, data = vitC)
##
## Residuals:
## Min 1Q Median 3Q Max
## -57.74 -15.42 5.81 18.61 35.36
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 48.644 2.598 18.726 < 2e-16 ***
## ctakersYes 22.093 5.716 3.865 0.000209 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 22.19 on 90 degrees of freedom
## Multiple R-squared: 0.1424, Adjusted R-squared: 0.1328
## F-statistic: 14.94 on 1 and 90 DF, p-value: 0.0002094## 2.5 % 97.5 %
## (Intercept) 43.48306 53.80461
## ctakersYes 10.73684 33.44917血清维生素C 浓度与在服用补充剂的人中较高,与不服用补充剂的人相比,服用者的血清维生素C 浓度平均高\(22.1 \:\mu\text{mol/L, 95% CI: } (10.7, 33.4)\),这个浓度差具有显著统计学意义\((p=0.00021)\)。
- 拟合一个多元线性回归模型,因变量为血清维生素 C 浓度,预测变量使用 性别,吸烟状态,和 是否服用维生素补充剂。解释输出结果的数字的含义。跟这些预测变量单独和血清维生素 C 浓度建立的简单线性回归模型作比较。说明哪些结果发生了改变,为什么。
##
## Call:
## lm(formula = seruvitc ~ sex + cigs + ctakers, data = vitC)
##
## Residuals:
## Min 1Q Median 3Q Max
## -40.656 -19.068 2.244 17.620 38.028
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 44.972 3.545 12.686 < 2e-16 ***
## sexWomen 10.658 4.514 2.361 0.020439 *
## cigsSmoker -11.567 6.659 -1.737 0.085865 .
## ctakersYes 20.251 5.515 3.672 0.000413 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 21.27 on 88 degrees of freedom
## Multiple R-squared: 0.2296, Adjusted R-squared: 0.2033
## F-statistic: 8.742 on 3 and 88 DF, p-value: 3.884e-05## Analysis of Variance Table
##
## Response: seruvitc
## Df Sum Sq Mean Sq F value Pr(>F)
## sex 1 4270 4270.0 9.4354 0.0028320 **
## cigs 1 1497 1497.0 3.3080 0.0723454 .
## ctakers 1 6102 6101.8 13.4831 0.0004125 ***
## Residuals 88 39824 452.5
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## 2.5 % 97.5 %
## (Intercept) 37.927129 52.017379
## sexWomen 1.686636 19.629637
## cigsSmoker -24.799261 1.665767
## ctakersYes 9.290800 31.210572从这个多元线性回归的输出报告来看,血清维生素 C 浓度
- 在吸烟者中较低 \(-11.6 \:\mu\text{mol/L, 95% CI:} (-24.8, +1.67), p = 0.086\);
- 在女性中较高 \(+10.7 \:\mu\text{mol/L, 95% CI:} (1.69, 19.6), p = 0.020\);
- 在服用维生素补充剂的人中较高 \(+20.3 \:\mu\text{mol/L, 95% CI:} (9.29, 31.2), p = 0.0004\)。
故,本次数据告诉我们,服用维生素补充剂是最强的预测变量。在多元线性回归模型的结果中可以看到:
- 性别之间维生素 C 浓度差变小了 (\(+13.6 \rightarrow +10.7\))
这是因为女性中有较多人服用维生素补充剂。即便如此,性别差在多元线性回归模型中仍然是有意义的。
a <- Epi::stat.table(list("Vitamin C taker"=ctakers, "Gender" = sex), list(count(),percent(ctakers)), data = vitC, margins = TRUE)
print(a, digits = c(percent = 2))## ----------------------------------
## ---------Gender----------
## Vitamin Men Women Total
## C taker
## ----------------------------------
## No 37 36 73
## 84.09 75.00 79.35
##
## Yes 7 12 19
## 15.91 25.00 20.65
##
##
## Total 44 48 92
## 100.00 100.00 100.00
## ----------------------------------- 吸烟与非吸烟者之间的维生素C 浓度差也变小了(\(-14.8 \rightarrow -11.6\)),因为尽管吸烟与非吸烟者的维生素补充剂服用比例差不不大,但是吸烟者中大部分是男性。 (详见下表)
吸烟者和非吸烟者之间维生素 C 浓度差经过多元线性回归调整后变得不再有统计学意义 \((p=0.086)\)。
a <- Epi::stat.table(list("Vitamin C taker"=ctakers, "Smoker" = cigs), list(count(),percent(ctakers)), data = vitC, margins = TRUE)
print(a, digits = c(percent = 2))## -------------------------------------
## -----------Smoker-----------
## Vitamin Non-smoker Smoker Total
## C taker
## -------------------------------------
## No 63 10 73
## 78.75 83.33 79.35
##
## Yes 17 2 19
## 21.25 16.67 20.65
##
##
## Total 80 12 92
## 100.00 100.00 100.00
## -------------------------------------a <- Epi::stat.table(list("Gender" = sex, "Smoker" = cigs), list(count(),percent(sex)), data = vitC, margins = TRUE)
print(a, digits = c(percent = 2))## ------------------------------------
## -----------Smoker-----------
## Gender Non-smoker Smoker Total
## ------------------------------------
## Men 36 8 44
## 45.00 66.67 47.83
##
## Women 44 4 48
## 55.00 33.33 52.17
##
##
## Total 80 12 92
## 100.00 100.00 100.00
## ------------------------------------- 在前一个模型中加入年龄,身高,体重作为新的预测变量。先解释新的模型中报告的个数值的意义,利用方差分析表格比较两个模型的差别 (先手计算,再用 R 计算确认你的答案)。
由于身高体重有缺损值(serial=24),所以要比较预测变量增加前后的模型,需要先把之前的模型中 serial=24 的观察对象删除掉才公平。
##
## Call:
## lm(formula = seruvitc ~ sex + cigs + ctakers, data = vitC[-24,
## ])
##
## Residuals:
## Min 1Q Median 3Q Max
## -40.792 -18.208 2.208 17.590 36.972
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 46.028 3.552 12.960 < 2e-16 ***
## sexWomen 9.764 4.487 2.176 0.032277 *
## cigsSmoker -12.255 6.589 -1.860 0.066266 .
## ctakersYes 19.832 5.453 3.637 0.000467 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 21.01 on 87 degrees of freedom
## Multiple R-squared: 0.2259, Adjusted R-squared: 0.1992
## F-statistic: 8.461 on 3 and 87 DF, p-value: 5.394e-05## Analysis of Variance Table
##
## Response: seruvitc
## Df Sum Sq Mean Sq F value Pr(>F)
## sex 1 3689 3688.5 8.3528 0.0048609 **
## cigs 1 1679 1679.1 3.8024 0.0543987 .
## ctakers 1 5841 5841.0 13.2272 0.0004669 ***
## Residuals 87 38418 441.6
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Model2 <- lm(seruvitc ~ sex + cigs + ctakers + age + weight + height, data = vitC[-24,])
summary(Model2);anova(Model2)##
## Call:
## lm(formula = seruvitc ~ sex + cigs + ctakers + age + weight +
## height, data = vitC[-24, ])
##
## Residuals:
## Min 1Q Median 3Q Max
## -40.561 -17.718 4.229 18.747 35.584
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 65.3516 89.4816 0.730 0.467217
## sexWomen 10.3666 7.2848 1.423 0.158428
## cigsSmoker -11.7996 6.7574 -1.746 0.084439 .
## ctakersYes 19.8593 5.5473 3.580 0.000574 ***
## age -0.3533 0.8397 -0.421 0.674988
## weight 0.1073 0.2231 0.481 0.631741
## height -1.5730 42.2590 -0.037 0.970396
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 21.29 on 84 degrees of freedom
## Multiple R-squared: 0.2327, Adjusted R-squared: 0.1779
## F-statistic: 4.245 on 6 and 84 DF, p-value: 0.0008801## Analysis of Variance Table
##
## Response: seruvitc
## Df Sum Sq Mean Sq F value Pr(>F)
## sex 1 3689 3688.5 8.1366 0.0054597 **
## cigs 1 1679 1679.1 3.7040 0.0576682 .
## ctakers 1 5841 5841.0 12.8848 0.0005562 ***
## age 1 205 205.3 0.4529 0.5028317
## weight 1 133 133.0 0.2934 0.5895062
## height 1 1 0.6 0.0014 0.9703964
## Residuals 84 38079 453.3
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1利用偏 \(F\) 检验的公式
\[ F=\frac{(205.2889295+132.9899543+0.6280691)/3}{38079.42/84} = 0.2492713 \]
## Analysis of Variance Table
##
## Model 1: seruvitc ~ sex + cigs + ctakers
## Model 2: seruvitc ~ sex + cigs + ctakers + age + weight + height
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 87 38418
## 2 84 38079 3 338.91 0.2492 0.8617所以检验统计量对应的\(p=0.86\) 告诉我们没有证明据证明调整了性别,吸烟状况,服用补充剂与否之后,增加的年龄,体重,身高作为预测变量和观察对象的血清维生素C 浓度有关系。模型 2 比模型 1 不能解释更多的模型残差 (不比模型 1 更加拟合数据)。
27.5.2 红细胞容积与血红蛋白
| Variable name | content |
|---|---|
hb
|
Haemoglobin (gm/dl) |
pcv
|
Pack cell volume % |
age
|
Age (years) |
- 把数据导入 R,并且建立因变量为血红蛋白,预测变量为 PCV 和 年龄的多元线性回归模型
## vars n mean sd median trimmed mad min max range skew kurtosis se
## hb 1 12 12.53 1.70 12.8 12.56 1.70 9.6 15.1 5.5 -0.26 -1.39 0.49
## pcv 2 12 38.58 8.14 37.5 38.80 11.12 25.0 50.0 25.0 -0.10 -1.59 2.35
## age 3 12 32.75 8.98 31.5 32.40 9.64 20.0 49.0 29.0 0.31 -1.20 2.59##
## Call:
## lm(formula = hb ~ pcv + age, data = haem)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.4134 -1.0023 0.3025 0.6622 1.8674
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.06057 1.96798 2.571 0.0301 *
## pcv 0.10557 0.04285 2.463 0.0360 *
## age 0.10355 0.03887 2.664 0.0259 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.146 on 9 degrees of freedom
## Multiple R-squared: 0.6298, Adjusted R-squared: 0.5475
## F-statistic: 7.655 on 2 and 9 DF, p-value: 0.01143## # A tibble: 12 × 5
## hb pcv age e_hat y_hat
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 11.1 35 20 0.274 10.8
## 2 10.7 45 22 -1.39 12.1
## 3 12.4 47 25 -0.211 12.6
## 4 14 50 28 0.762 13.2
## 5 13.1 31 28 1.87 11.2
## 6 10.5 30 31 -0.938 11.4
## 7 9.6 25 32 -1.41 11.0
## 8 12.5 33 35 0.331 12.2
## 9 13.5 35 38 0.810 12.7
## 10 13.9 40 40 0.475 13.4
## 11 15.1 45 45 0.629 14.5
## 12 13.9 47 49 -1.20 15.1- 利用 R 的矩阵计算重现回归模型的计算结果
- 计算因变量和两个预测变量各自的和
- 计算因变量和两个预测变量各自的平方和
sumy2 <- sum((haem$hb)^2)
sumx1y <- sum(haem$hb*haem$pcv)
sumx2y <- sum(haem$hb*haem$age)
sumx12 <- sum((haem$pcv)^2)
sumx22 <- sum((haem$age)^2)
sumx1x2 <- sum(haem$pcv*haem$age)- 生成一个数值为 1 的变量,名为
one
- 用
matrix()命令生成矩阵
Rownames <- NULL
for(i in 1:12) {
a <- paste("row", i, sep = "")
Rownames <- c(Rownames,a); rm(a)
}
Y <- matrix(haem$hb ,dimnames = list(Rownames, "hb"))
Y## hb
## row1 11.1
## row2 10.7
## row3 12.4
## row4 14.0
## row5 13.1
## row6 10.5
## row7 9.6
## row8 12.5
## row9 13.5
## row10 13.9
## row11 15.1
## row12 13.9X <- matrix(c(one, haem$pcv, haem$age), nrow = 12, dimnames = list(Rownames, c("one", "pcv", "age")))
X## one pcv age
## row1 1 35 20
## row2 1 45 22
## row3 1 47 25
## row4 1 50 28
## row5 1 31 28
## row6 1 30 31
## row7 1 25 32
## row8 1 33 35
## row9 1 35 38
## row10 1 40 40
## row11 1 45 45
## row12 1 47 49- 用公式 (27.4) 计算估计 \(\mathbf{\hat\beta}\) 矩阵
XX <- t(X) %*% X # these are the sum of squares of each variable and the sum of the cross products of the pairs of variables
XX## one pcv age
## one 12 463 393
## pcv 463 18593 15276
## age 393 15276 13757## sumx1 sumx12 sumx2 sumx22 sumx1x2
## 1 463 18593 393 13757 15276## hb
## one 150.3
## pcv 5887.7
## age 5026.0## sumy sumx1y sumx2y
## 1 150.3 5887.7 5026## hb
## one 5.0605666
## pcv 0.1055671
## age 0.1035513## hb
## one 5.0605666
## pcv 0.1055671
## age 0.1035513可以看到 betahat 的结果和多元回归模型输出的回归系数估计是一致的。
- 计算拟合值
## hb
## row1 10.82644
## row2 12.08921
## row3 12.61100
## row4 13.23836
## row5 11.23258
## row6 11.43767
## row7 11.01338
## row8 12.16857
## row9 12.69036
## row10 13.42530
## row11 14.47089
## row12 15.09623- 估计回归系数的方差协方差矩阵
## hb
## row1 0.2735607
## row2 -1.3892125
## row3 -0.2110005
## row4 0.7616445
## row5 1.8674188
## row6 -0.9376680
## row7 -1.4133839
## row8 0.3314258
## row9 0.8096378
## row10 0.4746999
## row11 0.6291083
## row12 -1.1962310## hb
## hb 11.81094## [,1]
## hb 1.312327# multiply the inverse of the cross-product matrix for the predictors
# by the residual variance to get the variance-covariance matrix of
# the coefficients
V <- solve( crossprod(X) ) * as.numeric(Sigma2)
V## one pcv age
## one 3.87296385 -0.0632072065 -0.0404536966
## pcv -0.06320721 0.0018365202 -0.0002336447
## age -0.04045370 -0.0002336447 0.0015104882# the square root of the diagonal terms in the above matrix are the standard errors shown in the regression output
sqrt(diag(V))## one pcv age
## 1.96798472 0.04285464 0.03886500