第 43 章 评价模型的表现
在广义线性回归的模型表现中,还有几个重要的概念,精准度(calibration),变异度(variation),和分辨能力(descrimination),本章继续用二进制结果变量和多个共变量的广义线性回归模型来理解这几个概念。本章使用逻辑回归,也就是 \(\text{logit}\) 链接方程的 GLM 来解释,但是实际上使用其他链接方程时,这些概念也是一样通用的。
当用逻辑回归模型拟合了观测数据。我们可以通过拟合的模型来计算每个观测对象的预测“成功”概率 (the predicted probability of “success” for each subject)。当使用 \(\text{logit}\) 作链接方程时,每个人的预测概率 (predicted probability) 为:
\[ \hat\pi_i = \frac{\text{exp}(\hat\alpha + \hat\beta_1x_{i1} + \cdots + \hat\beta_px_{ip})}{1+\text{exp}(\hat \alpha + \hat\beta_1x_{i1} + \cdots + \hat\beta_px_{ip})} \]
43.1 精准度 calibration
模型具有良好的精准度时,其计算获得的每个观测对象的预测概率,和每个观测对象本身“成功”的概率期望值保持一致。
\[ E(Y|\hat\pi = p) = p \]
当一个 GLM 具有良好精准度时,我们可以利用它在临床医学中发挥重要的作用 (如预测患者死亡,发病或疗效等)。如果模型的精准度不佳,那可能导致的严重后果有:治疗不必要治疗的“健康人”,或者漏掉应该治疗的“患者”。当一个模型的预测变量只包含了分类型变量,比较观测概率和预测概率的过程较为简单,比较各个分类变量的排列组合后,不同共变量类型(covariate pattern) 的患者的观测值和预测值即可。
这里再沿用之前 NHANES 的重度饮酒相关的数据 (Section 42.4)来继续下面对精准度的说明,先拟合一个只有性别作为预测变量的逻辑回归模型:
library(haven)
library(tidyverse)
NHANES <- read_dta("../Datas/nhanesglm.dta")
NHANES <- NHANES %>%
mutate(Gender = ifelse(gender == 1, "Male", "Female")) %>%
mutate(Gender = factor(Gender, levels = c("Male", "Female")))
with(NHANES, table(Gender))Gender
Male Female
1391 1157 NHANES <- mutate(NHANES, Heavydrinker = ALQ130 > 5)
Model_perf <- glm(Heavydrinker ~ Gender, data = NHANES, family = binomial(link = "logit"))
epiDisplay::logistic.display(Model_perf)
Logistic regression predicting Heavydrinker
OR(95%CI) P(Wald's test) P(LR-test)
Gender: Female vs Male 0.17 (0.12,0.24) < 0.001 < 0.001
Log-likelihood = -834.1079
No. of observations = 2548
AIC value = 1672.2158完成这个模型之后,在STATA 里可以用简便的estat gof, table 命令获取模型拟合的观测值和期待值表格,然而R 里面需要用到LogisticDx 包里的诊断命令dx 获取~~~~:
GenderFemale y P n yhat
1: 0 249 0.17900791 1391 249
2: 1 42 0.03630078 1157 42# obtain Pearson's test statistics
chi2 <- sum((LogisticDx::dx(Model_perf)$sPr)^2)
pval <- pchisq(chi2, 1, lower.tail=FALSE)
data.frame(test="Pearson chi2(1)",chi.sq=chi2,pvalue=pval) test chi.sq pvalue
1 Pearson chi2(1) 2.388904e-25 1在这个只有性别作预测变量的逻辑回归模型里,当然只有男,女,两种共变量模式 (covariate patterns)。此时,模型的精准度100% (y 是观测值, yhat 是期待值)。接下来,再在模型中加入一个是否体重超重的二进制变量。再获取其观测值和期待值表格如下:
NHANES <- mutate(NHANES, highbmi = bmi > 25)
Model_perf <- glm(Heavydrinker ~ Gender + highbmi, data = NHANES, family = binomial)
epiDisplay::logistic.display(Model_perf)
Logistic regression predicting Heavydrinker
crude OR(95%CI) adj. OR(95%CI) P(Wald's test)
Gender: Female vs Male 0.17 (0.12,0.24) 0.17 (0.12,0.24) < 0.001
highbmi 1.21 (0.93,1.58) 1.11 (0.84,1.46) 0.456
P(LR-test)
Gender: Female vs Male < 0.001
highbmi 0.453
Log-likelihood = -833.8269
No. of observations = 2548
AIC value = 1673.6539 GenderFemale highbmiTRUE y P n yhat
1: 0 1 175 0.18366250 961 176.49966
2: 0 0 74 0.16860543 430 72.50034
3: 1 1 29 0.03762016 731 27.50034
4: 1 0 13 0.03403677 426 14.49966# obtain Pearson's test statistics
chi2 <- sum((LogisticDx::dx(Model_perf)$sPr)^2)
pval <- pchisq(chi2, 1, lower.tail=FALSE)
data.frame(test="Pearson chi2(1)",chi.sq=chi2,pvalue=pval) test chi.sq pvalue
1 Pearson chi2(1) 0.2988186 0.584624此时的模型有 4 种共变量模式 (covariate patterns),其实就是性别和超重与否的四种排列组合。这里报告的 Pearson's test statisitics
我们在前一章讲逻辑回归残差的部分有讲过,它就是 Pearson 标准化残差的平方和。此处它的卡方检验,检验零假设是“模型制定正确”。所以,我们无足够的证据 \((p=0.58)\) 来反对零假设,数据观测值和模型的期待值似乎也较为吻合。
但是一旦模型里加入了新的连续型变量,整个模型的共变量模式(covariate patterns),将会变得很难进行上面的观测值和期待值的比较,由于加入的连续型变量会导致模型的共变量模式变得越来越多,甚至接近与样本量个数\(n\),也就是每个共变量模式的样本越来越小,直至等于\(1\)。连续型变量的模型中我们 Hosmer-Lemeshow 检验 (Section 36.4) 而不是 Pearson 统计检验量。
43.2 可解释因变量的变异度及 \(R^2\) 决定系数
精准度的确重要,但是模型精准度好,只代表它和过去拟合它的观测数据之间关系接近,不代表它能准确地预测其他的个体的概率。前文中只有性别作为预测变量的逻辑回归模型就是实例,它和拟合的观测数据做到了100% 完美拟合,但是不用大脑思考也知道,除了性别还有其他更多的能预测一个人是否是重度饮酒者的变量,且拥有能提升模型的拟合程度的潜质。只有性别作预测变量的逻辑回归模型,最大的问题在于,它只能解释个体之间重度饮酒者概率的变异度(variation)中极少的部分。事实上,它只能解释能够用性别解释的个体之间重度饮酒者概率的变异度。所以,此处打算引伸出的概念就是类似简单线性回归中的 \(R^2\) 决定系数 (Section 25.2.3) 的定义。
你应该还能记得,在简单线性回归中决定系数 \(R^2\) 的含义是因变量的平方和 (平方和) 中能被模型解释的部分:
\[ R^2 = \frac{SS_{REG}}{SS_{yy}} = \frac{\sum_{i=1}^n(\hat{y}_i-\bar{y})^2}{\ sum_{i=1}^n(y_i-\bar{y})^2} = 1-\frac{\sum_{i=1}^n(y_i-\hat{y}_i)^2}{\ sum_{i=1}^n(y_i-\bar{y})^2} \]
许多前人尝试过试图将线性回归的决定系数概念扩展到广义线性回归模型中来,但是目前为止的尝试都不太成功。所以,只有一些借鉴了简单线性回归的的决定系数思想的概念,得到了扩展,但是要注意,他们本身和决定系数是有区别的。
“假决定系数(pseudo-R2)”,别名McFadden 的似然比系数(McFadden’s likelihood ratio index)
\[R^r_{\text{McFadden}} = 1 - \frac{\ ell_c}{\ell_\text{null}}\]
其中\(\ell_c, \ell_{\text{null}}\) 分别是模型的极大似然值和零模型时的极大似然值。
假决定系数,之所以被冠名“假”,因为这个系数你也可以在简单线性回归下计算,但是其大小常常和一般我们熟知的决定系数结果有些差距。所以,常有人质疑其到底是否可用 (因为它在现实生活中根本不可能取到 \(0\) 或 \(1\))。
在 R 里,拟合了逻辑回归以后通常也不会报告假决定系数值的大小。所以想要获得它,需要 DescTools::PseudoR2() 命令来获取:
McFadden
0.07875219 上文中包含了性别和是否超重的模型的假决定系数只有区区 \(0.0785\),可见,只有性别和是否超重两个变量只能解释结果变量变异度中极少的部分。
43.3 分辨能力 descrimination
43.3.1 敏感度和特异度
评价一个逻辑回归的表现,最后的一个手段是,看这个模型对观测对象的分辨能力。也就是,当我们人为地指定一个概率值\(p\) 作为是否患病的阈值,那么,观测对象通过模型计算获得的概率,已经观测对象本身的观测概率之间,其实可以用诊断学的敏感度和特异度的概念来评价模型对于观测对象的分别能力到底如何。所以逻辑回归模型的敏感度就是,病例中通过模型计算被判断为阳性的概率;特异度是,非病例中,通过模型计算本判断为阴性的概率。这个敏感度特异度当然会随着我们选择的阈值而变化。
图 43.1 所示的是,将性别, BMI,和年龄三个变量放入逻辑回归模型之后,模型对于观察对象的分辨能力的 ROC 示意图。计算所得的 ROC 曲线下面积为 0.7484。如果一个模型是失败的,那么其曲线下面积为 (接近) 0.5。也就是会十分贴近 \(y=x\) 的直线。
Model_perf <- glm(Heavydrinker ~ Gender + bmi + ageyrs, data = NHANES, family = binomial)
ROC_graph <- epiDisplay::lroc(Model_perf, grid.col = "grey", lwd = 3, frame = FALSE)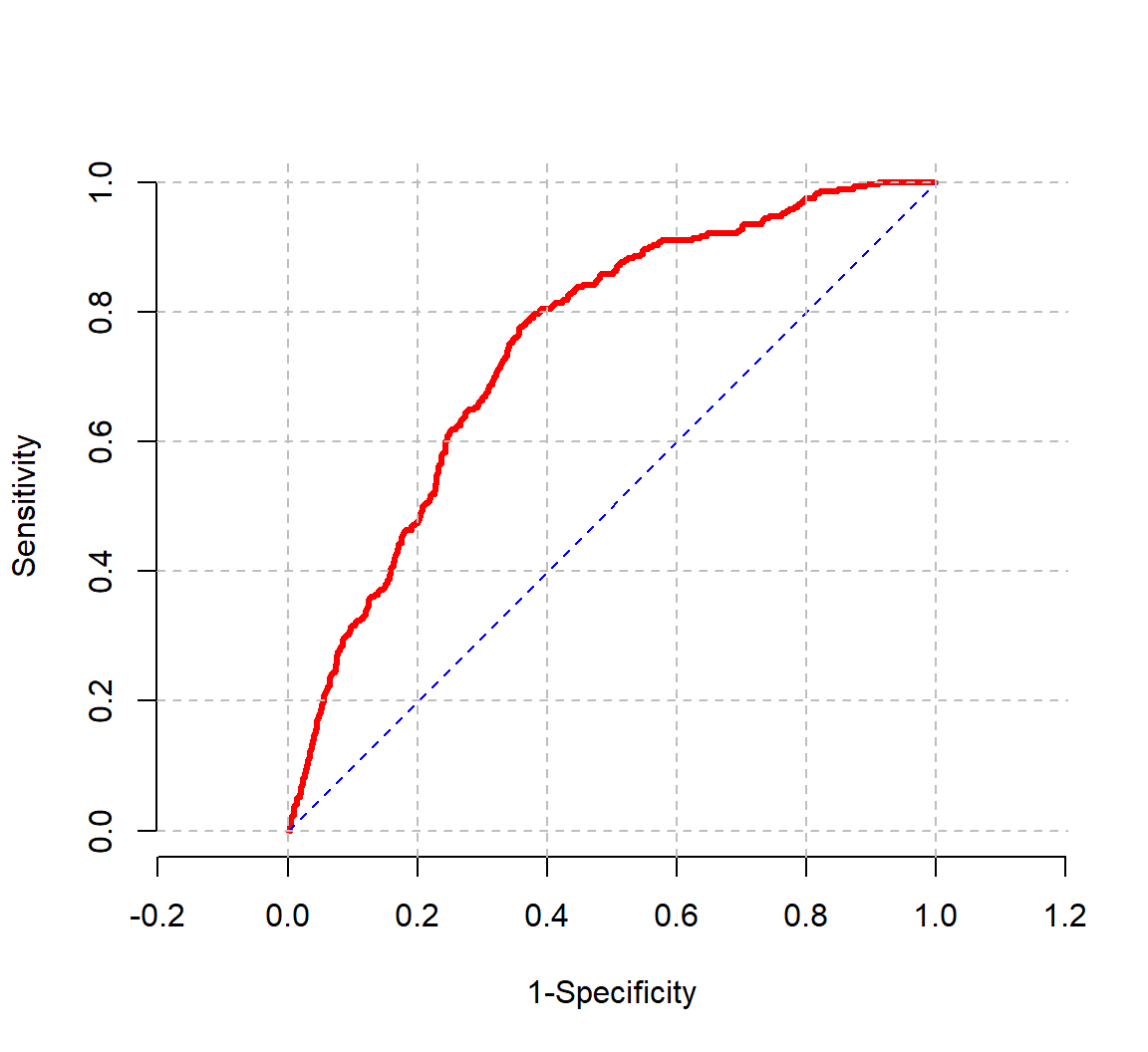
图 43.1: Receiver operating curve for model for heavy drinking with gender, age, and BMI
[1] 0.748353曲线下面积,AUC 的另一个有用的意义是,从观测对象中任意选取两个人,一个是病例 \((y_i = 1)\),一个是非病例 \((y_j = 0)\),那么曲线下面积就是模型能够正确将这两个对象按照是否患病的可能性进行排序的概率。 \(\text{AUC} = \text{Pr}(\pi_i > \pi_j | y_i = 1 \& y_j = 0)\)
ROC 曲线本身有自己的优点,也有许多局限性。最近有另外一个用于诊断的新型曲线–预测曲线(Pepe et al. 2007)。预测曲线绘制的是,观测对象的拟合后概率 \(\hat\pi_i\) 和这个概率在所有观察对象的拟合后概率的百分位数 (percentile) 之间的曲线。一个模型,如果给许多对象相似的概率,那么不能说这个模型的分辨能力足够好。同时,此图也能一目了然让人看到大概多少对象的患病概率是大于一定水平的。
Predictive <- data.frame(fitted(Model_perf), rank(fitted(Model_perf))/2548)
names(Predictive) <- c("hatpi", "percentile")
ggplot(Predictive, aes(x = percentile, y = hatpi)) + geom_line() +
ylim(0, 0.4) +
labs(x = "Risk percentile", y = "Heavy drinker risk") + theme_bw() +
theme(axis.title = element_text(size = 17),
axis.text.x = element_text(size = 15),
axis.text.y = element_text(size = 15))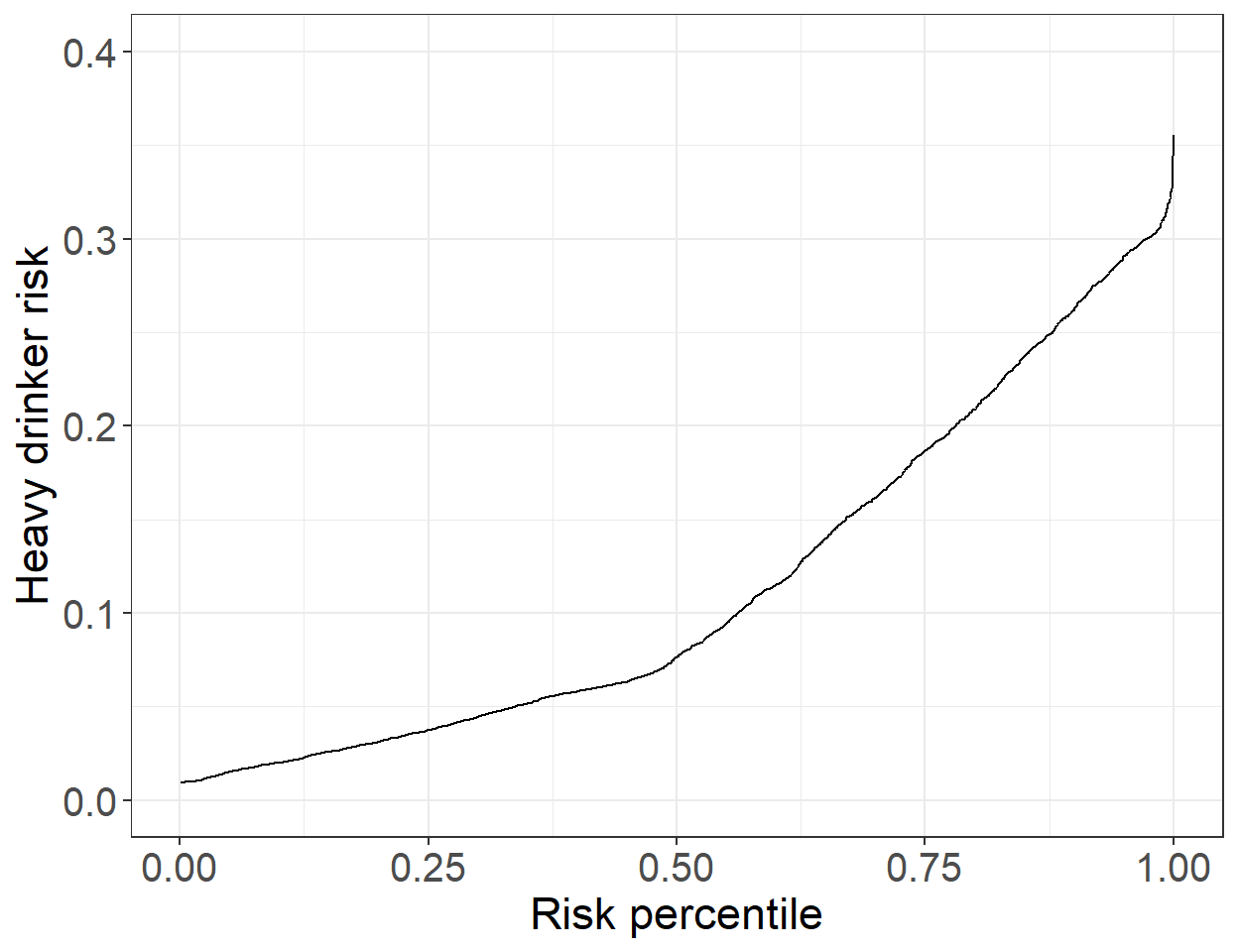
图 43.2: Predictiveness curve for model for heavy drinking with gender, age, and BMI as covariate
图 43.2 所示的是,性别,年龄,BMI作为共变量的逻辑回归模型的预测变量,预测重度饮酒概率的模型给出的预测曲线。从图中可见,大多数人的概率值各不相同。而且,图中也能告诉我们大约 20% 的观测对象其重度饮酒的概率大于 0.2。