第 25 章 方差分析
25.1 背景
当我们用统计模型模拟真实数据的时候,我们常常会被问到这样的问题:“两个模型哪个能更好的拟合这个数据?”
本章我们先考虑简单的情况,两个模型互相比较时,其中一个稍微简单些的模型使用的预测变量,同时也是另一个较复杂的模型的预测变量 (nested models)。所以,复杂模型的预测变量较多,而其中一个或者几个预测变量又构成了新的较为简单的模型。这两个模型之间的比较,就需要用到方差分析 Analysis of Variance (ANOVA)。
此处方差分析的原则是:如果复杂模型能够更好的拟合真实实验数据,那我们会认为简单模型无法解释的大量残差平方和,有效地被复杂模型解释了。所以,这一原则下,可以推理,复杂模型计算获得的残差平方和,会显著地小于简单模型计算获得的残差平方和。 ANOVA 就提供了这个残差平方和变化的定量比较方法。
25.2 简单线性回归模型的方差分析
其实从线性回归的第一章节开始,我们都在使用方差分析的思想。图 23.1 数据的回归模型中,我们其实比较了以下两个模型:
- 零假设模型:null model, 即认为年龄和体重之间没有任何关系 (水平直线);
- 替代模型: alternative model, 认为年龄和体重之间有一定的线性关系 (拟合后的直线)。
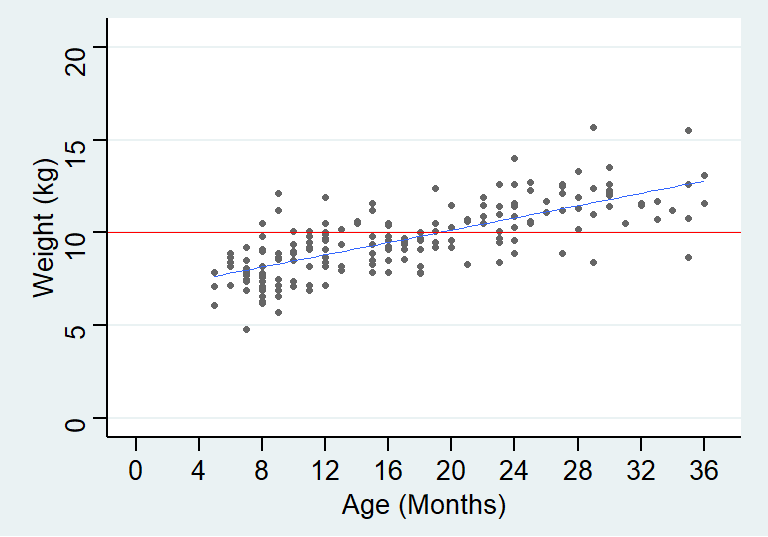
图 25.1: NULL (red) and Alternative models (blue) for the data
25.2.1 两个模型的参数估计
无论是零假设模型,还是替代假设模型,都需要通过最小化残差来获得其参数估计:
\[ SS_{RES} = \sum_{i=1}^n \hat\varepsilon^2= \sum_{i=1}^n(y_i-\hat y_i)^2 \]
替代假设模型,在线性回归第一部分(Section 23.3.1) 已经提到过,均值方程是\(E(Y|X=x) = \alpha+\beta x\),且这个方程的参数\(\ alpha, \beta\) 以及残差方差\(\sigma^2\) 的估计值计算公式也已经推导完成(23.5) (23.6) (23.9)。
零假设模型,它的均值方程是 \(E(Y|X=x)=\alpha\)。所以需要将它的残差最小化:
\[ SS_{RES} = \sum_{i=1}^n(y_i-\hat\alpha)^2 \]
由于 (23.5) :\(\hat\alpha=\bar{y}-\hat\beta\),所以 \(\hat\alpha = \bar{y}\)。
所以对于零假设模型来说:
\[ SS_{RES} = \sum_{i=1}^n(y_i-\bar{y})^2 =SS_{yy} \]
因此,没有预测变量的零假设模型,它的残差平方和,就等于因变量的平方和。
25.2.2 分割零假设模型的残差平方和
ANOVA,方差分析的原则,其实就是将较简单模型 (零假设模型) 的残差平方和 \((SS_{RES_{NULL}})\),分割成下面两个部分:
- 替代假设的复杂模型能够说明的模型平方和 \((SS_{REG})\);
- 替代假设的复杂模型的残差平方和 \((SS_{RES_{ALT}})\)。
用数学表达式表示为:
\[ \begin{equation} \sum_{i=1}^n(y_i-\bar{y})^2 = \sum_{i=1}^n(\hat{y}-\bar{y})^2 + \sum_{i =1}^n(y_i-\hat{y}_i)^2 \\ SS_{RES_{NULL}}(SS_{yy}) = SS_{REG} + SS_{RES_{ALT}} \end{equation} \tag{25.1} \]
证明
\[ \begin{aligned} \sum_{i=1}^n(y_i-\bar{y})^2 &= \sum_{i=1}^n[(\hat{y}-\bar{y})+(y_i-\ hat{y})]^2\\ &= \sum_{i=1}^n(\hat{y}-\bar{y})^2+\sum_{i=1}^n(y_i-\hat{y})^2+2\ sum_{i=1}^n(\hat{y}_i-\bar{y})(y_i-\hat{y}) \\ &= SS_{REG} + SS_{RES_{ALT}} + 2\sum_{i=1}^n(\hat{y}_i-\bar{y})(y_i-\hat{y}) \end{aligned} \]
接下来就是要证明 \(\sum_{i=1}^n(\hat{y}_i-\bar{y})(y_i-\hat{y})=0\)
因为公式 (24.1) \(\hat{y}_i=\bar{y}+\hat{\beta}(x_i-\bar{x})\) 所以公式变形如下:
\[ \begin{aligned} \sum_{i=1}^n(\hat{y}_i-\bar{y})(y_i-\hat{y}) &= \sum_{i=1}^n(\bar{y}+ \hat\beta(x_i-\bar{x})-\bar{y})(y_i-\bar{y}-\hat\beta(x_i-\bar{x})) \\ &= \sum_{i=1}^n\hat\beta(x_i-\bar{x})[y_i-\bar{y}-\hat\beta(x_i-\bar{x})] \\ &= \hat\beta\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y}) - \hat\beta^2\sum_{i=1}^n( x_i-\bar{x}) \\ &= \frac{S_{xy}}{S_{xx}}S_{xy} - (\frac{S_{xy}}{S_{xx}})^2SS_{xx}\\ &= 0 \\ \Rightarrow SS_{RES_{NULL}}(SS_{yy}) &= SS_{REG} + SS_{RES_{ALT}} \end{aligned} \]
25.2.3 \(R^2\) – 我的名字叫决定系数
在公式(25.1) 中,因变量的平方和被分割成了两个部分:\(SS_{REG}\) 回归模型能说明的部分,和\(SS_{RES_{ALT}}\)回归模型的残差平方和。所以,我们定义回归模型能说明的部分,占因变量平方和的百分比 \(\frac{SS_{REG}}{SS_{yy}}\),为决定系数 \(R^2\)。
这个决定系数之前 (Section 24.5) 也出现过:
\[ \begin{equation} R^2 = \frac{SS_{REG}}{SS_{yy}} = \frac{\sum_{i=1}^n(\hat{y}_i-\bar{y})^2}{\ sum_{i=1}^n(y_i-\bar{y})^2} = 1-\frac{\sum_{i=1}^n(y_i-\hat{y}_i)^2}{\ sum_{i=1}^n(y_i-\bar{y})^2} \end{equation} \tag{25.2} \]
再一次回到数据 (23.1) 的线性回归来看:
growgam1 <- read_dta("../Datas/growgam1.dta")
Model <- lm(wt~age, data=growgam1)
print(summary(Model), digit=6)##
## Call:
## lm(formula = wt ~ age, data = growgam1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.924182 -0.784889 0.007099 0.797468 4.067806
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.8375842 0.2100701 32.5491 < 2.22e-16 ***
## age 0.1653314 0.0111115 14.8793 < 2.22e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.27352 on 188 degrees of freedom
## Multiple R-squared: 0.540782, Adjusted R-squared: 0.53834
## F-statistic: 221.392 on 1 and 188 DF, p-value: < 2.22e-16R 输出的结果中最下面的部分 Multiple R-squared: 0.5408。我们就可以用“人话”来解释其意义:假定年龄和体重成直线关系,那么年龄解释了这组数据中儿童体重变化 (平方和) 的 54%。
25.2.4 方差分析表格 the ANOVA table
一般情况下一个简单线性回归,通过 ANOVA 对因变量平方和的分割,会被汇总成下面这样的表格:
表格中最右边一列是平均平方和 (mean sum of squares)。它的定义是将平方和除以各自的自由度。其中残差的平均平方和 \(MS_{RES}=\frac{SS_{RES}}{(n-2)}\) 是替代模型下残差方差的无偏估计。总体平均平方和 (total mean sum of squares),则是零假设模型时的残差方差估计。在 R 里面也已经演示过多次 anova(model) 是调取方差分析表格的代码:
## Analysis of Variance Table
##
## Response: wt
## Df Sum Sq Mean Sq F value Pr(>F)
## age 1 359.06320 359.06320 221.39203 < 2.22e-16 ***
## Residuals 188 304.90655 1.62184
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1注意到 R 省略掉第三行总体平方和的部分,不过其实也不太需要。检验统计量 F 的计算也很简单,就是359.06320/1.62184=221.39。
25.2.5 用 ANOVA 进行假设检验
在 ANOVA 中使用的检验手段是 \(F\) 检验。这里用\(F\) 检验来比较模型解释的因变量平方和部分 \((SS_{REG})\) 和这个模型不能解释的残差平方和部分 \(SS_{RES}\) 经过自由度校正以后比值的大小。
此时我们需要知道零假设和替代假设\(\text{H}_0: \beta=0 \text{ v.s. H}_1: \beta\neq0\) 时,\(SS_{REG}, SS_{RES}\) 的分布。
- 零假设和替代假设时,\(SS_{RES}\) 均服从自由度为 \(n-2\) 的卡方分布:
\[ \begin{equation} \text{Because } SS_{RES} = \sum_{i=1}^n \varepsilon \sim N(0, \sigma^2)\\ \frac{SS_{RES}}{\sigma^2} \sim \chi^2_{n-2} \end{equation} \tag{25.3} \]
- 零假设时, \(SS_{REG}\) 服从自由度为 \(1\) 的卡方分布,且与 \(SS_{RES}\) 相互独立:
\[ \begin{equation} \frac{SS_{REG}}{\sigma^2} \sim \chi^2_1 \end{equation} \tag{25.4} \]
- 替代假设时,\(SS_{REG}\) 服从一个非中心化的卡方检验,且与 \(SS_{RES}\) 相互独立:
\[ \begin{equation} SS_{REG} = \beta^2 SS_{xx} + U \text{ where }\frac{U}{\sigma^2} \sim \chi_1^2 \end{equation} \tag{25.5} \]
25.2.6 简单线性回归时的 \(F\) 检验
如果两个随机变量各自服从相应自由度的卡方分布,他们的每个元素的比值服从 \(F\) 分布:
\[ A\sim \chi_a^2 \text{ and } B\sim \chi_b^2\\ \Rightarrow \frac{A/a}{B/b} \sim F_{a,b} \]
因此,目前为止的推导过程我们也可以看到,在零假设条件下,\(MS_{REG}\) 和\(MS_{RES}\) 的比值会服从\(F\) 分布,自由度为\((1, n- 2)\):
\[ \begin{equation} F=\frac{SS_{REG}/1}{SS_{RES}/(n-2)} = \frac{MS_{REG}}{MS_{RES}} \sim F_{1,n-2} \end{equation} \tag{25.6} \]
在替代假设条件下\((\text{H}_1: \beta\neq0)\),\(SS_{REG}\) 的期望值是\(\sigma^2+\beta^2SS_{xx}\),所以替代假设条件下的\(F\) 检验量总是会大于零假设时的\(F\)。因此你可以看到,这是一个双侧检验(\(\text{H}_0: \beta=0 \text{ v.s. H}_1: \beta\neq0\)),但是由于替代假设的\(F\) 总是较大,所以只需要\(F\) 的右半部分的概率密度积分(单侧\(p\) 值)。
25.2.7 简单线性回归时 \(F\) 检验和 \(t\) 检验的一致性
证明
\[ \begin{aligned} &F=\frac{SS_{REG}/1}{SS_{RES}/(n-2)} = \frac{SS_{REG}}{(SS_{yy}-SS_{REG})/(n-2 )} \\ &\text{Since } r^2 = \frac{SS_{REG}}{SS_{yy}} \\ &F=(n-2)\frac{SS_{yy}r^2}{SS_{yy}-SS_{yy}r^2}=(n-2)(\frac{r^2}{1-r ^2})=t^2 \end{aligned} \]
最后一步用到 (Section 24.6) 证明过的,回归系数检验统计量 \(t\),和 Pearson 相关系数 \(r\) 之间的关系。
25.3 分类变量用作预测变量时的 ANOVA
方差分析的应用是如此的广泛,你可以在多重回归中使用,也可以在模型中有分类变量时使用,甚至是同时有连续性变量和分类变量的回归模型中得到应用。
之前也遇到过二分类变量的简单线性回归模型,当时我们的做法是使用一个哑变量来表示一个二分类变量。同样的方法也可以用到多组分类变量上来,然后继续使用线性回归。
25.3.1 一个二分类预测变量
在前面的例子(Section 23.7) 中也已经展示过,可以通过线性回归来分析一个二分类变量(实验组对照组),和一个连续型变量(能直立行走时的儿童年龄)两个变量之间的关系。而且其结果同两样本 \(t\) 检验的结果完全一致。
继续回到之前用过的这个儿童行走数据 (表 23.1):
##
## Call:
## lm(formula = Age ~ Group, data = Walk)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.1250 -0.7375 -0.3750 0.3875 2.8750
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.12500 0.51223 19.7663 1.007e-08 ***
## Groupcontrol 2.22500 0.75977 2.9285 0.0168 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.2547 on 9 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.48795, Adjusted R-squared: 0.43105
## F-statistic: 8.5763 on 1 and 9 DF, p-value: 0.016797## Analysis of Variance Table
##
## Response: Age
## Df Sum Sq Mean Sq F value Pr(>F)
## Group 1 13.502 13.5017 8.5763 0.0168 *
## Residuals 9 14.169 1.5743
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1之前分析这个数据的时候也说明过了,这里的回归系数 \(2.225\) 的含义是两组之间均值的差异。而且注意看,这个回归系数是否为零的检验统计量\((t-test)\)获得的 \(p\) 值和 ANOVA 的检验结果 \((F-test)\) 也是一致的。正验证了我们前面证明的结果。 (Section 25.2.7)
25.3.2 一个模型,两种表述
上面这个例子中,一个二分类的预测变量和一个因变量之间的关系,实际上可以用两种数学模型来表达:
- 令\(y_i, x_i\) 分别是第\(i\) 名观察对象的因变量(“直立行走的年龄”),和预测变量(“实验组或者对照组”) \((i=1,\cdots, n)\)。那么回归模型可以写作:
\[ \begin{equation} y_i = \alpha+\beta x_i + \varepsilon_i, \text{ where } \varepsilon_i \sim NID(0, \sigma^2) \end{equation} \tag{25.7} \]
其中,
- \(x_i=0\) 时,表示第 \(i\) 名观察对象在实验组;
- \(x_i=1\) 时,表示第 \(i\) 名观察对象在对照组。
在这样的回归模型标记下,零假设和替代假设分别是 \(\text{H}_0: \beta=0 \text{ v.s. H}_1: \beta\neq0\)
- 另一种模型的表达方式,被叫做 ANOVA 表达方式。是如此描述上面的关系的:令\(y_{ki}\) 表示第\(i\) 名观察对象,他在第\(k\) 组\((i=1,\cdots, n_k; k=1,2)\),此时的模型被写作:
\[ \begin{equation} y_{ki} = \mu_k + \varepsilon_{ki}, \text{ where } \varepsilon_{ki} \sim NID(0, \sigma^2) \end{equation} \tag{25.8} \]
此时,\(\mu_k\) 表示第 \(k\) 组因变量的均值。零假设和替代假设分别是 \(\text{H}_0: \mu_k=\mu \text{ v.s. H}_1: \mu_k\neq\mu\)。这里的 \(\mu\) 表示,每个组的平均值等于一个共同的均值 \(\mu\)。
25.3.3 分组变量的平方和
对于预测变量只有一个分组变量的模型,拟合后的数值就是两组的因变量均值 \((\bar{y}_k)\)。在零假设条件下,两组均值相等,均等于总体均值 \(\bar{y}\)。这就导致了,残差平方和,模型平方和在分组变量的 ANOVA 分析时要使用与连续型变量不同的术语。
- 残差平方和表示为:
\[ \begin{equation} SS_{RES} = \sum_{k=1}^k\sum_{i=1}^{n_k} (y_{ki}-\bar{y}_k)^2 \end{equation} \tag{25.9} \]
其实这就是组内平方和 (within group sum of squares)。
- 模型平方和表示为:
\[ \begin{equation} SS_{REG} = \sum_{k=1}^k\sum_{i=1}^{n_k}(\bar{y}_k-\bar{y})^2=\sum_{k=1}^ kn_k(\bar{y}_k-\bar{y})^2 \end{equation} \tag{25.10} \]
其实这就是组间平方和 (between group sum of squares)
## Df Sum Sq Mean Sq F value Pr(>F)
## Group 1 13.5017 13.50170 8.57629 0.016797 *
## Residuals 9 14.1687 1.57431
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 1 observation deleted due to missingness其实这跟之前的 anova(Model) 给出的结果完全一致。
##
## Bartlett test of homogeneity of variances
##
## data: Age by Group
## Bartlett's K-squared = 0.6302, df = 1, p-value = 0.4273FYI. 上面的代码 bartlett.test() 利用的是另外一个叫做 Bartlett 检验法的方差比较公式。 (在 STATA 的 oneway 命令中也会默认给出 Bartlett 检验的方差是否一致的检验结果)
25.3.4 简单模型的分组变量大于两组的情况
公式 (25.8), (25.9), 和 (25.10) 在两组以上分组变量作预测变量时也是适用的。但是当组数为 \(K\) 时,组内平方和 (残差平方和 \(SS_{RES}\)) 的自由度需要修改成 \(n-K\) (这是因为模型中使用了 \(K\) 个参数)。此时方差分析 ANOVA 的汇总表格就变为了下面这样:
此时,检验统计量 \(F\) 的计算公式为:
\[ \begin{equation} F=\frac{SS_{between}/(K-1)}{SS_{within}/(n-K)} \sim F_{(K-1),(n-K)} \end{equation} \tag{25.11} \]
在解释两组以上分组变量的分析结果时,要注意的是如果\(p\) 值很小,检验结果告诉我们的是,各组中因变量的均值不全相等,而不是全部都不相等。其实就是,即使做了这个检验,我们也不知道到底那两组之间是有差异的。如果此时我们发现结果提示均值不全相等,通常我们还会再作进一步的分析,使用类似成对比较法等等 (以后再继续详述)。不过提前要记住,如果使用成对比较法时(pair-wise comparisons),多重比较的问题(multiple comparisons)会凸显出来,主要的结果是增加统计检验的假阳性(false-positive ) 概率,此时再继续使用\(p<0.05\) 作为统计学意义的标准则是不妥当的。