第 15 章 假设检验的近似方法

15.1 近似和精确检验

前一章描述了如何用对数似然比寻找最佳检验统计量 (Section 14.3)。一旦找到并确定了最佳检验统计量，接下去还需要确定这个最佳检验统计量的样本分布，用定好的显著性水平(\(\alpha=0.05\))确定拒绝域，再使用观察数据计算数据本身的统计量，然后对反对零假设的证据定量(计算\(p\) 值) 。前一章用的例子均来自于正态分布，所以我们都能够不太复杂地获得样本均值，样本方差等较容易取得样本分布的检验统计量。正如我们在前一章最后部分 (Section 14.7 ) 总结的那样，大多数情况下我们没有那么幸运。最佳检验统计量的样本分布会很难确定。所以另一个进行假设检验的途径就是近似检验法 (approximate tests)。

15.2 精确检验法之

记得我们之前说到，简单假设\(H_0: \theta=\theta_0\text{ v.s. } H_1: \theta=\theta_1\) 的检验的最佳检验统计量可以使用Neyman-Pearson lemma (尼曼皮尔森辅助定理) (Section 14.3 ) 来确定：

\[\ell_{H_0}-\ell_{H_1} = \ell(\theta_0)-\ell(\theta_1)\]

如果假设变成了复合型假设：\(H_0: \theta\in\omega_0 \text{ v.s. } H_1: \theta\in\omega_1\)。此时，\(\omega_0, \omega_1\) 分别指两种假设条件下我们关心的总体参数的可能取值范围。那么可以把上面的定理扩展成，在 \(\omega_0, \omega_1\) 两个取值范围内，零假设和对立假设在给出的观察数据条件下的极大似然之比：

\[\text{log}\frac{\text{max}_{H_0}[L(\theta|data)]}{\text{max}_{H_1}[L(\theta|data)]}= \text{max}_{H_0}[\ell(\theta|data)]-\text{max}_{H_1}[\ell(\theta|data)]\\ =\text{max}_{\theta\in\omega_0}[\ell(\theta|data)]-\text{max}_{\theta\in\omega_1}[\ell(\theta|data)] \]

典型的假设检验情况下，我们面对的是简单的零假设和复合型的替代假设：

\[H_0: \theta=\theta_0 \text{ v.s. } H_1: \theta\neq\theta_0\]

所以在这个情况下，套用扩展以后的 Neyman-Pearson lemma：

\[\text{max}_{H_0}[\ell(\theta)]-\text{max}_{H_1}[\ell(\theta)]=\ell(\theta_0) - \ell(\hat \theta)=llr(\theta_0)\]

之前讨论对数似然比 (Section 13.3 ) 时我们已知：

\[\text{Under }H_0: \theta=\theta_0\Rightarrow -2llr(\theta_0)\stackrel{\cdot}{\sim}\mathcal{X}_1^2\]

于是利用自由度为 \(1\) 的卡方检验的特征我们就可以为反对零假设的证据定量，计算关键的拒绝域。如果说显著性水平为 \(\alpha\) 那么，我们拒绝零假设 \(H_0:\theta=\theta_0\) 的拒绝域是：

\[-2llr(\theta_0)>\mathcal{X}^2_{1,1-\alpha}\]

当使用 \(\alpha=0.05\) 时，这个关键的拒绝域就是：\(-2llr(\theta_0)>3.84\)。

这就是传说中的 (对数) 似然比检验，(log-)Likelihood ratio test (LRT)。

LRT 的优点：

  1. 简单；
  2. \(p\) 值不会被参数尺度(parameter scale) 左右，也就是说如果我们对参数进行了数学转换也不会影响似然比检验计算得到的\(p\) 值大小。

LRT 的缺点：

  1. 非正态分布的数据时，LRT 只能算是渐进有效 (asymptotic valid)，即样本量要足够大时结果才能令人满意；
  2. 无法总是保证这是最佳检验统计量；
  3. 需要计算两次对数似然 (MLE 和 零假设时)。

15.3 近似检验法之 – Wald 检验

和 LRT 一样， Wald 检验也适用于检验 \(H_0: \theta=\theta_0 \text{ v.s. } H_1: \theta\neq\theta_0\)。但是本方法其实是使用对数似然比方程的近似二次方程 (Section ??)。相比之下，LRT 使用的是精确的对数似然比，只对检验统计量 \(-2llr\) 进行了自由度为 \(1\) 的卡方分布 \(\mathcal{X}_1^2\) 近似。本节介绍的 Wald 检验过程中使用了两次近似，一次是计算对数似然比时使用了二次方程，一次则是和 LRT 一样对检验统计量进行 \(\mathcal{X}_1^2\) 近似。

根据对数似然比近似结论 ：

\[llr(\theta)\approx-\frac{1}{2}(\frac{M-\theta}{S})^2\text{ asymptotically}\]

其中，\(M\) 是\(\text{MLE }\hat\theta\)，\(S=\sqrt{\left.-\frac{1}{\ell^{\prime\prime}(\theta)}\right \vert_{\theta=\hat{\theta}}}\)

而且前一节我们也看到，

\[ \text{Under }H_0: \theta=\theta_0\Rightarrow -2llr(\theta_0) \stackrel{\cdot}{\sim}\mathcal{X}_1^2\\ \Rightarrow -2\times-\frac{1}{2}(\frac{M-\theta_0}{S})^2 \stackrel{\cdot}{\sim}\mathcal{X}_1^2 \\ \Rightarrow (\frac{M-\theta_0}{S}) \stackrel{\cdot}{\sim} N(0,1)\\ \text{Let } W=(\frac{M-\theta_0}{S}) \]

\(W\) 就是我们在 Wald 检验中用到的检验统计量。接下来就可以计算给定显著水平 \(\alpha\) 时的拒绝域，给 \(p\) 值定量：

当\(W>N(0,1)_{1-\alpha/2}\) 或\(W<N(0,1)_{\alpha/2}\)时，拒绝\(H_0: \theta=\theta_0\) ；

或者，当 \(W^2>\mathcal{X}^2_{1,1-\alpha}\) 时，拒绝 \(H_0: \theta=\theta_0\)。

这就是我们心心念念的 Wald 检验。

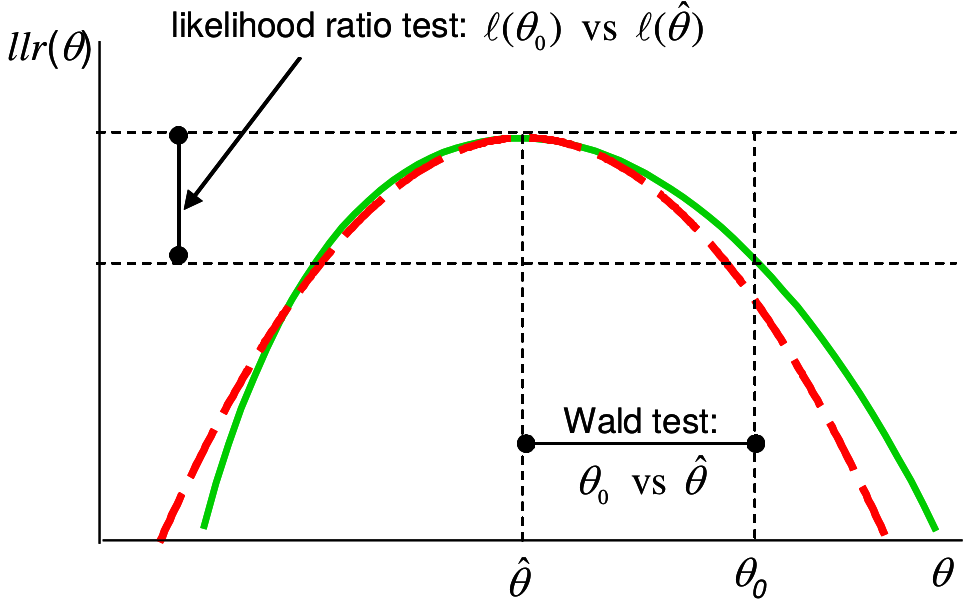
Likelihood ratio and Wald tests: solid (green) line is log-likelihood ratio, dashed ( red) is quadratic approximation

图 15.1: Likelihood ratio and Wald tests: solid (green) line is log-likelihood ratio, dashed ( red) is quadratic approximation

上图 15.1 解释了 LRT 和 Wald 检验的不同之处。红色虚线是二次方程，用于近似似然比方程(绿色实线) 。二者在 \(\text{MLE}=\hat\theta\) 时同时取极大值。 Wald 检验的是，数据提供的 \(\hat\theta\) 和我们想要比较的零假设 \(\theta_0\) 之间的横轴差距。在检验量 \(W\) 中我们还把这个差除以观察数据均值的标准差(数据的标准误) 。如果数据本身波动大，\(W\) 的分母(标准误) 较大，那么即使 \(\hat\theta - \theta_0\) 保持不变，统计量变小，反对零假设的证据也就越小。反观，LRT 检验的检验统计量就是上图 15.1 显示的纵轴差 \(\ell(\theta_0)-\ell(\hat\theta)\) 的大小。二者之间的关系被直观的显示在图中。

Wald 检验优点：

  1. 比 LRT 略简单；
  2. 不必再计算零假设时的对数似然，只需要 \(MLE\) 和它的标准误。

Wald 检验缺点：

  1. 两次近似(LRT只用了一次近似) ；
  2. 无法总是保证这是最佳检验统计量；
  3. 参数如果被数学转换 ，\(p\) 值会跟着变化。

15.4 近似检验法之 – Score 检验

注意到 Wald 检验使用的近似二次方程是在 MLE， 也就是极大似然比时的点 \(\hat\theta\) 和对数似然比方程取相同的值和相同曲率 (二次导数)。 可以类比的是，Score 检验是基于另一种二次方程模拟，Score 检验的近似二次方程和对数似然比方程在零假设 (\(\theta_0\)) 时取相同的曲率。所以，Score 检验使用的近似方程在 \(\theta_0\) 时和对数似然比方程在相同位置时的倾斜度 (一阶导数)，和曲率 (坡度的变化程度，二阶导数) 相同。所以令 \(U\) 为对数似然比方程在 \(\theta_0\) 时的坡度，定义 \(V\) 是对数似然比方程在 \(\theta_0\) 时的曲率的负数：

\[ \begin{aligned} & U=\ell^\prime(\theta)|_{\theta=\theta_0}=\ell^\prime(\theta_0)\\ & V=-E[\ell^{\prime\prime}(\theta)]|_{\theta=\theta_0}=-E[\ell^{\prime\prime}(\theta_0)] \end{aligned} \]

注：此处的 \(V=-E[l^{\prime\prime}(\theta_0)]\) 又常常被叫做 Expected Fisher information。

记得在 Wald 检验中使用的近似方程： \[llr(\theta)\approx-\frac{1}{2}(\frac{M-\theta}{S})^2\text{ asymptotically}\]

令 \(q(\theta)=-\frac{1}{2}(\frac{M-\theta}{S})^2\) 就有：

\[ \begin{aligned} & q^\prime(\theta) =\frac{M-\theta}{S^2}\\ & \Rightarrow q^\prime(\theta_0) =\frac{M-\theta_0}{S^2}\\ & q^{\prime\prime}(\theta) =-\frac{1}{S^2}\\ & \Rightarrow q^{\prime\prime}(\theta_0)=E[l^{\prime\prime}(\theta_0)]\\ & \Rightarrow \frac{1}{S^2} =-E[l^{\prime\prime}(\theta_0)]\\ & q^\prime(\theta_0) = \frac{M-\theta_0}{S^2} = -E[l^{\prime\prime}(\theta_0)](M-\theta_0)\\ & = \ell^\prime(\theta_0)\\ & \Rightarrow M-\theta_0 = -\frac{\ell^\prime(\theta_0)}{E[l^{\prime\prime}(\theta_0)]}\\ & \Rightarrow M = -\frac{\ell^\prime(\theta_0)}{E[l^{\prime\prime}(\theta_0)]}+\theta_0\\ & q(\theta)=-\frac{1}{2}(\frac{M-\theta}{S})^2=\frac{E[l^{\prime\prime}(\theta_0)]}{2}(-\frac{\ell^\prime(\theta_0)}{E[l^{\prime\prime}(\theta_0)]}+\theta_0-\theta)^2\\ & q(\theta)=-\frac{V}{2}(\frac{U}{V}+\theta_0-\theta)^2\\ & \Rightarrow \text{ Under } H_0: \theta=\theta_0\\ & \Rightarrow q(\theta_0)=-\frac{V}{2}(\frac{U}{V})^2=-\frac{U^2}{2V}\\ & \Rightarrow -2q(\theta_0)=\frac{U^2}{V} \stackrel{\cdot}{\sim}\mathcal{X}_1^2\\ & \text{Or equivalently} \frac{U}{\sqrt{V}} \stackrel{\cdot}{\sim} N(0,1) \end{aligned} \]

这就是 Score 检验时使用的检验统计量。相应的拒绝域就可以被定义为： 当 \(\frac{U^2}{V}>\mathcal{X}_{1,1-\alpha}^2\) 时，拒绝 \(H_0\)

如下面的示意图15.2 所示，Score 检验，比较的是\(\theta_0\) 时的校正后似然方程的坡度(一阶导数/二阶导数)，和极大似然时的坡度(一阶导数=0) 的差别。如果这个值越大，说明零假设时的似然和极大似然 (观察数据的信息) 的距离越远，拒绝零假设的证据就越有力。

Score test: solid (green) line is log-likelihood ratio, dashed (red) is quadratic approximation

图 15.2: Score test: solid (green) line is log-likelihood ratio, dashed (red) is quadratic approximation

Score 检验优点：

  1. 比 LRT 简单；
  2. 不需要计算 MLE，只需要计算零假设时的对数似然比方程之坡度和曲率；
  3. 在流行病学用到的检验方法中最常用，也最容易扩展 (Mantel-Haenszel test, log rank test, generalised linear models such as logistic, Poisson, Cox regressions)。

Score 检验缺点：

  1. 和 Wald 检验一样用到了两次近似；
  2. 无法总是保证这是最佳检验统计量；
  3. 参数如果被数学转换 ，\(p\) 值会跟着变化。

15.5 LRT, Wald, Score 检验三者的比较

  1. LRT 比较的是对数似然方程在零假设\(H_0\) 和极大似然估计(MLE) 时之间的纵轴差(图15.1)；Wald 检验试图直接比较MLE 和\(H_0\) 的横轴差(二次方程近似法，并用标准误校正) (图15.1)；Score 检验比较的是对数似然方程在\(H_0\) 时的切线斜率(二次方程近似法，用曲率也就是二阶导数校正) (图15.2)。三种检验比较的东西各不相同，但是这种差距大到进入拒绝域时，数据就会拒绝零假设。其中 Score 检验的计算过程最为简便，只需要计算 \(H_0\) 时对数似然方程的一阶和二阶导数，而不用去计算 MLE，因此更多的被应用在流行病学数据计算中。

  2. 如果对数似然方程本身就是左右对称的 (正态分布的情况下)，这三个检验方法计算的所有结果都是完全一致的。如果对数似然方程只是近似左右对称，那么三者的计算结果会十分接近。可以说，三种检验方法是渐进等价的。

  3. 如果对观测值进行了数学转换，三者中只有 LRT 的计算结果保持不变。如果对参数的数学转换使得对数似然方程更加接近左右对称的二次方程，那么 Wald 和 Score 检验的计算结果可以得到改善。

  4. 如果说，MLE 和 零假设之间的差距很大，那么 Wald 或者 Score 检验所使用的二次方程近似法的误差会增加，此时倾向于使用 LRT 来进行精确检验。当然如果当样本量较大，要检验的差距也很大，三种检验方案都能够提供证据拒绝零假设 (\(p\) 值都会很小)。

  5. 如果三种检验方案给出的计算结果迥异，即使使用了数学转换结果也没有明显改善的话，那么最大的问题是样本量太小。这时候还是老老实实用 LRT 吧。

  6. 几乎所有的参数检验都归类与这章节介绍的三种检验方法。比如说 \(Z\) 检验， \(t\) 检验， \(F\) 检验都是 LRT。在流行病学研究中最常用的还是 Score 检验。

我们的结论是，当条件允许的情况下，统计检验都推荐尽量使用精确检验 LRT。